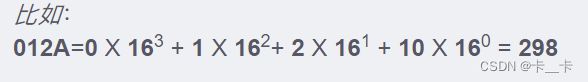2-2基础算法-递归/进制转换

一.递归

1.数的计算

评测系统

#include 
int countCombinations(int n) { //计算当然组合种数
    if (n == 1) {
        return 1;
    }
    int count = 1;//数字本身就是一个有效组合
    for (int i = 1; i <= n / 2; i++) {
        count += countCombinations(i);//自身+当前数所产生的组合种数
    }
    return count;
}
using namespace std;
int main()
{
    int n;
    cin >> n;
    cout<<countCombinations(n);
}

2.计算函数值

#include
using namespace std;
int s(int x) {
    if (x == 0)
        return 1;
    else if (x % 2 == 0) {
        return s(x / 2);
    }
    else {
        return s(x - 1) + 1;
    }
}
int main() {
    int x;
    cin >> x;
    cout << s(x);
}

3.约瑟夫环

评测系统

#include 
using namespace std;
int f(int n,int k){
  if(n==1)
    return 1;
  else
    return (f(n-1,k)+k-1)%n+1;
}
int main()
{
  int n,k;
  cin>>n>>k;
  cout<<f(n,k);
  return 0;
}

4.金额查错


评测系统

解析：假设错误的总金额是 100 元，而明细账目清单上的金额总和是 120 元，那么可能遗漏的金额组合应该总和为 20 元，因为 120 - 100 = 20。题目要求找出所有可能的组合，使得这些组合的金额总和为 20 元。

第一次：count作为金额求和的结果，寻找可行的子串

#include 
#include 
using namespace std;
void f(int i, int sum, int count, vector<int>& a, vector<int>& subset, vector<vector<int>>& result) {
    if (sum == count) {
        result.push_back(subset);
        return;
    }
    if (i == a.size() || sum > count) {
        return;
    }
    subset.push_back(a[i]);
    f(i + 1, sum + a[i], count, a, subset, result);//包含当前元素

    subset.pop_back();//不包含当前元素
    f(i + 1, sum, count, a, subset, result);
}
int main()
{
    int total,n;
    cin >> total>> n;
    vector<int> a(n);
    int sum = 0;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        sum += a[i];
    }
    int count=sum - total;
    vector<vector<int>> result;//存放最终结果
    vector<int> subset;//寻找满足条件的子集
    f(0, 0, count, a, subset, result);
    for (const auto& x : result) {
        for (int x2 : x) {
            cout << x2 << " ";
        }
        cout << endl;
    }
}

再考虑次序和去重问题，得到最终代码

#include 
#include 
#include 
using namespace std;
void f(int i, int sum, int count, vector<int>& a, vector<int>& subset, vector<vector<int>>& result) {
    if (sum == count) {
        result.push_back(subset);
        return;
    }
    if (i == a.size() || sum > count) {
        return;
    }
    for (int j = i; j < a.size(); ++j) {
        if (j > i && a[j] == a[j - 1])
            continue;
        subset.push_back(a[j]);
        f(j + 1, sum + a[j], count, a, subset, result);
        subset.pop_back();
    }
}
int main()
{
    int total,n;
    cin >> total>> n;
    vector<int> a(n);
    int sum = 0;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        sum += a[i];
    }
    sort(a.begin(), a.end());//排序
    int count=sum - total;
    vector<vector<int>> result;//存放最终结果
    vector<int> subset;//寻找满足条件的子集
    f(0, 0, count, a, subset, result);
    for (const auto& x : result) {
        for (int x2 : x) {
            cout << x2 << " ";
        }
        cout << endl;
    }
}

二.进制转换

1.任意进制转十进制：x=xk+a

如十六转十

评测系统

#include 
using namespace std;
int main()
{
    string s = "2021ABCD";
    int a[100];//存放十六进制的每个数
    for (int i = 0; i < s.length(); i++) { //调整十六进制数
        if (s[i] >= '0' && s[i] <= '9') {
            a[i] = s[i]-'0';
        }
        else {
            a[i] = 10+s[i] - 'A';
        }
    }
    int x=0;//输出的十进制数
    for (int i = 0; i < s.length(); i++) { //【转换代码】
        x = x * 16 + a[i];
    }
    cout << x;
}

2.十进制转任意进制：通过数组a输出

while(x){
	a[cnt++]=x%k;
	x=x/k;
}
reverse(a,a+cnt);

评测系统

#include 
#include 
#include 
using namespace std;
int main()
{
    int T;
    cin >> T;
    while (T--) {
        int N, M;
        cin >> N >> M;
        string s;
        cin >> s;
        long long int a[100];
        
        //【先转成十进制】
        for (int i = 0; i < s.length(); i++) {
            if (s[i] >= '0' && s[i] <= '9') {
                a[i] = s[i] - '0';
            }
            else {
                a[i] = 10 + s[i] - 'A';
            }
        }
        long long int x = 0;//输出的十进制数
        for (int i = 0; i < s.length(); i++) {
            x = x * N + a[i];
        }
        if (M == 10) {
            cout << x << endl;
        }
        else { //【十进制转M进制】
            string b[100];
            int cnt = 0;
            while (x) {
                if (x % M >= 10) {
                    b[cnt++] = x % M - 10 + 'A';
                }
                else
                    b[cnt++] = to_string(x % M);
                x = x / M;
            }
            reverse(b, b + cnt);//翻转

            //输出
            for (int i = 0; i < cnt; i++) {
                cout << b[i];
            }
            cout << endl;
        }
    }
}