【论文阅读】Reachability Queries with Label and Substructure Constraints on Knowledge Graphs

Wan X, Wang H. Reachability Queries With Label and Substructure Constraints on Knowledge Graphs[J]. IEEE Transactions on Knowledge and Data Engineering, 2022.

Abstract

由于知识图（KGs）描述和建模了现实世界中实体和概念之间的关系，因此对KGs的推理通常对应于具有标签和实体的可达性查询穿刺约束（LSCR）。特别地，对于搜索路径p，LSCR查询不仅要求p传递的边的标签在一个特定的标签集中，而且还声称p中的一个顶点可以坐着是某个子结构约束。LSCR查询比标签约束可达性（LCR）查询要复杂得多，而且对于kg上的LSCR查询没有有效的解决方案我们的知识。在此基础上，我们对kg、UIS和INS上的查询提出了两种解决方案。前者也可以用于一般的边标记图，并且相对方便实际的实现。后者是一种有效的基于局部索引的知情搜索策略。对合成和真实kg的广泛实验评估表明，说明了我们的解决方案可以有效地处理kg上的LSCR查询。

1 INTRODUCTION

现在，许多高度格式化的数据库被用来构建领域特定的KGs [21]，其推理被广泛应用于各种应用中，如犯罪链接分析[15]、[16]、sus恶性交易检测[12]、电子商务推荐[10]等。在这样的应用程序中，两个实体之间的推理通常与具有标签和子结构的可达性查询有关约束[16]，[22]，作为KGs可以看作是边缘标记图。
例如，我们将一个金融KG建模为G，其中(i)每个顶点代表一个人；（ii）每条边（=，=）与一个账户转移或从顶点u到顶点v的关系相关；（iii）t他对e的标签要么是与转移发生的时间相对应的时间戳，要么是一种社会关系（例如，朋友、父母、结婚等）。在一些检测任务中，要验证生态系统嫌疑人C和嫌疑人P之间的正常犯罪关系，已知信息：“从C到P的间接交易发生在2019年4月，其中交易的中间人之一a艾米已经结婚了……”，如图1(a).所示

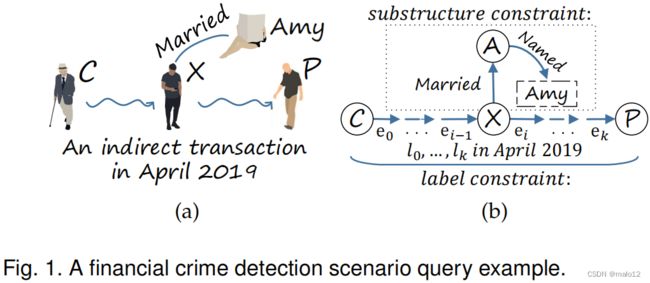
如果存在经济犯罪关系，交易路径p =< C，e0，v0，…，vk−1，ek，P>从C到P，如图1(b)所示，其中(i) l0，…，lk代表ed的标签…，0、…，，和10、…，lk的时间戳分别在2019年4月；（ii）∃X∈v0，…，vk−1，它是p的传递顶点之一，代表G中嫁给Amy的人。笔记G可以包含多对已婚夫妇，也许只有其中一些夫妇可以满足上述条件。
此外，这种查询也可以用于各种情况下，例如，特定于领域的交通导航[8]异常检测[3]等，提出以下问题：一个顶点s是否可以通过路径p到达一个顶点t，其中p中的边缘标签在某个标签集（标签约束）中，而p通过一个ce是否保留子结构（子结构约束）？
尽管KGs上的标签和子结构约束可达性（LSCR）查询对于上述推理任务非常有用，但据我们所知，目前还没有特定的解决方案。原因是LSCR问题比起源于[6]的标签约束可达性（LCR）问题要复杂得多。根据[6]的说法，对于LCR查询有两种技术，在线搜索（DFS/BFS）和完全传递闭包（TC）预计算。
前者可以直接应用于LCR查询。假设输入KG包含|V |顶点和|E|边，在LCR查询中应用的DFS/BFS的时间复杂度为O（|V | + |E|），作为实验室el约束修剪DFS/BFS的搜索空间。不幸的是，在kg上的LSCR查询问题过于复杂。如在第3节中所分析的，在最坏的情况下，为LSCR查询实现传统的BFS/DFS的时间复杂度约为O（V*(V+E)）来解决我们的问题。
后者的目标是预先计算输入图的完整TC，以有效地回答LCR查询，但是，为图G存储完整TC的空间复杂度是O（|V|2×2L），其中L是标签集o因此，[6]、[25]、[19]可以降低索引的空间复杂度一个输入图。然而，上述方法的索引时间复杂度太高，无法索引一个较大的KG，如第3.2节所述。请注意，在本文中，我们不考虑近似值LCR查询的技术，例如[17]，因为KG推理应用程序需要精确的结果，如上面的犯罪检测场景。
贡献。在本文中，我们提供了一个全面的研究LSCR查询的KGs与有效的解决方案。我们的工作克服了传统地标的实际难以忍受的索引时间索引方法[19]，具有局部索引。此外，我们通过开发一个，克服了算法（第4节）的低效，该算法实现了KGs上LSCR查询的子图匹配技术基于局部索引的方法搜索策略。通过详细的实验评估，我们的工作可以有效地解决KGs上的LSCR查询。
我们的主要贡献如下：
我们首先定义了带有标签和子结构约束的可达性查询问题，这是基于KGs的推理的基础。
我们为LSCR查询开发了一种未知搜索算法，名为UIS，名为UIS。它在一般标记图上有很大的实际实现潜力，因为UIS不太复杂，也不需要使用kg的任何特征。
然后，我们开发了一个实现SPARQL引擎[1]的直观想法，称为UIS∗，以解决LSCR查询并克服UIS的缺点。这是因为： (i)当前的KGs是基于st的和OWL [7]的形式，通常可以通过SPARQL访问；（ii）子结构约束可以用SPARQL表示（第2节）。
然后，我们提出了一种有效的知情搜索算法，即INS，具有一种新的索引，局部索引。INS可以打破未知搜索算法的固定搜索方向，并可以支持通过开发两个数据结构作为基于局部索引的条目的评估函数，使输入KG中的顶点具有优先级。
最后，我们在真实数据集和合成数据集上进行了广泛的实验，以评估所引入的搜索算法。实验结果表明，该搜索算法能够有效地解决KGs上的LSCR查询。
本文的其余部分组织如下。在第2节中正式定义了KGs上的LSCR查询问题。我们分别在第3节、第4节和第5节中介绍了UIS、UIS∗和INS.实验结果见第6节。最后，我们在第7节中得出一个结论。

2 PROBLEM DEFINITION

我们正式定义了在KGs上的LSCR查询，其中使用了一个包含常用符号的表（表1）和两个KG示意图视图（图2和图3）。

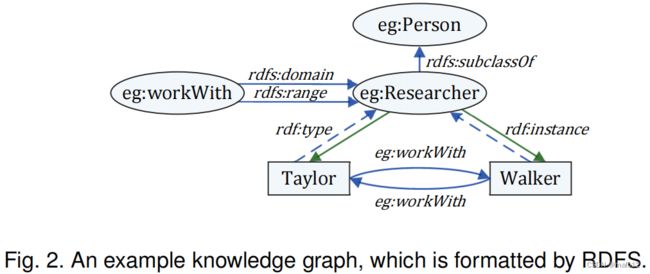
知识关系图谱（KG）。本质上，KGs [2]，[18]是由顶点和标记边组成的图。然而，与普通的边标记图不同，KGs往往对应于丰富的信息真实的世界，kg的大小相对较大。例如，在2014年底，自由基地[2]包括6800万个实体，10亿条关系信息和超过24亿个事实三倍。在practice，KGs由RDF三元组[11]存储，并由RDFS [5]（RDF模式）格式化。RDFS定义了一组具有特殊含义的RDF词汇表（例如：“rdfs：类”、“rdfs：子类”、“rdf：type”）可以构建RDF资源并格式化知识表示。从图分类的角度来看，RDFS将KGs表示为无标度网络[20]，其中具有一定程度的顶点的相对共性大大超过了平均值。
图2绘制了一个简单的带有一些RDF词汇表的KG，其中(i)“例如：研究人员”代表了现实世界中的一类研究者；（ii）“例如：workWith”是一个边缘标签实体，而边标记为“例如：workWith”的事件（“rdfs：域”），也指向（“rdfs：范围”）的一个实例“例如：研究者”；（iii）泰勒和沃克是真实的人和所有的研究人员(“e”的实例g:他们也一起工作（边缘标记为“例如：workWith”）。当然，在KGs中，一个与真实单词实例对应的顶点u具有很高的程度，比如“如：研究者”。此外，类顶点，如“eg：Person”对于KG结构来说，它比一个实例顶点更重要，例如，“例如：研究员”。
总之，KGs基本上是边缘标记的图，以RDF的形式，由RDFS结构。KG的正式定义见定义2.1。
定义2.1。知识图G是一个四重图（V，E，L，LS），其中： (1) V是G的顶点集，L是边标签集；(2) E⊆V×L×V是G的标记边集，对于∀e∈E，e = (s，l，t)是从s到t的边，带有标签l；(3)让λ： E→L是一个标签映射函数，即λ(e) = l，然后L=S∀e∈E（λ(e)）；(4) LS固定G的RDFS三元组。
请注意，我们将根据输入的KG G=（V、E、L、LS）来说明以下定义。
标签约束。本文中的标签约束与KG G中L的一个子集有关，例如，在图3(a)中，标签约束可以是{friendsOf，follows}。

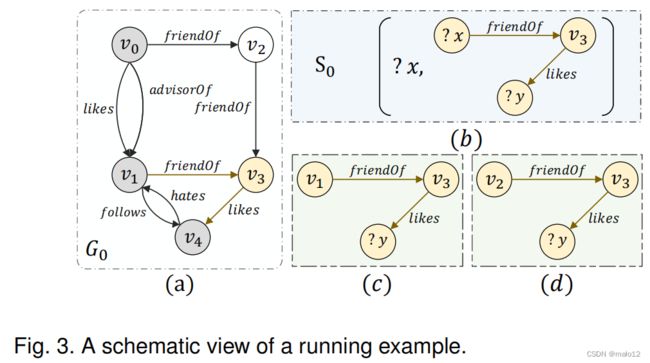
子结构约束。为了定义KG G中的子结构约束，我们首先将G中的一个可变子结构γ形式化为一个三重结构（Vγ，Eγ，E？），其中(i) Vγ⊆V，Eγ⊆E和∀(u，l，v)∈Eγ，u，v∈Vγ；（ii）E？={（u，l，？v）|u∈Vγ∧l∈L}∪{（？u，l，v）|v∈Vγ∧l∈L}，以及E中的一个元素e？然后，子结构约束定义如下:
定义2.2。子结构约束S是指一个元组（？x、VS、ES、E？），具体位置(VS、ES、E？）相符合到G中的可变子结构，以及∈？，e与？x或点？x。
例如，图3(b)展示了图3(a)中G0的子结构约束S0，其中S0 =（？x、{v3}、{}、{（？x、friendsOf、v3）、（v3、likes、？y）}）。
请注意，虽然子结构约束可以通过多种方式定义，但在本文中我们只研究使用最广泛的一种，其他形式可以从这个定义中推导出来。
可达性。为了清晰起见，我们让L §和V §分别表示路径p的标签集和顶点集，并让P（s，t）表示从一个顶点s到一个顶点t的所有路径的集合。反对显然，如果s到达t，则有一条从s到t的路径（P（s，t）=φ）。我们利用符号st和符号s9 t分别描述从顶点s到顶点t的可达性和非可达性。
标签约束的可达性（LCR）。类似地，如果一个顶点s在标签约束L（用sLt表示）下到达一个顶点t，则存在一条路径p形成s到t，其中p中的每个边标签都是L中一个元素，即L §⊆L。
相反，给定一个标签约束L，如果s L t，我们说L是一个充分的路径标签集。此外，如果∀L 0⊂L∧L 09 t，L是一个最小的充分路径标签集。为所有的the从s到t的最小充分路径标签集（CMS）用M（s、t）表示，并在定义2.3中定义。
定义2.3。一个标签集M（s，t）的集合是一个从s到t的CMS，iffM（s，t）={L（pi）|pi∈P（s，t）∧@ pj∈P（s，t），i = j，这样L（pj）⊂L（pi）}。
例如，M（v0、v3）={friendsOf}和M（v0、v4）={friendsOf,likes},{advisorOF,follows}，{likes,follows}如图3(a).所示
子结构约束的可达性。首先，我们假设一个顶点u满足一个子结构约束S=（？x，VS，ES，E？），如果我们将？x替换为u，其结果仍然是一个子结构或一个变量子结构例如，对于子结构约束S0（图3(b)）和两个顶点v1和v2，替换后的结果分别如图3©和图3(d)所示。由于v1和v2的替换结果是g0的可变子结构，因此v1和v2满足s0。
然后，如果一个顶点s在子结构约束S（用sSt表示）下到达一个顶点t，则有一个从s到t的路径p，其中∃u∈V§和u满足s。例如，在图3，v0 S0 v4，v0 S0 v3和v3 S0 v4。
全面的定理2.1给出了s L，S t存在的条件，该条件表明一个顶点s在一个标签约束L和一个子结构约束s下到达一个顶点t。例如，在F中igure 3(a)，给定一个标签约束L={喜欢，遵循}，v0 L，S 0 v4，而，v0 L，S90 v3。
定理2.1。KG G，iff，∃p∈（s，t），L §⊆L和∃u∈∧§满足。
证据第2.1条。通过上述的定义，可以很容易地证明这一点。
问题定义。根据上述定义，我们在定义2.4中定义了这个问题。
定义2.4。在KG G=（V，E，L，LS）上是一个四倍（s，t，L，S），其中s，t∈V，L⊆L，和S是G的子结构约束。如果s L，S t在G中，那么Q的答案是正确的。同样地，Q的答案是错误的。
附加。对于KG G和一个子结构约束S，我们让V（S，G）表示一个顶点集，它包含了G中满足子结构约束S的所有顶点。
此外，子结构约束S也可以用SPARQL[24]查询来表示。例如，S0（图3(b)）可以被建模为“Select？x，其中{？x< friends >v3”。v3< likes>?y.}".

3 UNINFORMED SEARCH

回答KGs上的可达性查询的最直接的方法是无知（盲）搜索策略[13]： DFS和BFS，它处理一个没有附加信息的输入查询d，在问题的定义中。只要使用标签约束来减少搜索空间，我们就可以采用DFS或BFS来解决LCR查询[6]。
不幸的是，LSCR查询太复杂了，而且DFS和BFS都不能直接用于这些查询，因为它们永远不会在查询处理中重新访问传递的顶点。例如，假体蛋白g标签约束L={喜欢，讨厌，友谊}，为了验证v3 L，S 0 v4的存在(a)，搜索算法需要走在路径p=，因为只有v1和v2才能满足s0。
要在KG G=（V、E、L、LS）上处理LSCR查询Q=（s、t、L、S），在DFS或BFS中至少需要两个过程。在标签const下的s可以到达其顶点的空间中进行搜索raint L；另一个只有当前者发现一个满足子结构约束S的顶点v时才能执行，并通过在v un可以到达的顶点上行走从v运行到t当前者停止或后者返回true时，此过程停止。
然后，我们分析了上述过程的时间复杂度，假设有一个子结构约束S=（？x，VS，ES，E？）。前一种程序需要O|V |(|VS|+|ES|+|E?|) +|E|计算每个传递的顶点是否能满足S。后一个过程的每个调用都需要O（|V |+|E|）。我们执行后者高达|V（S，G）|次，这是小于|V |。因此，我们总结了定理3.1中的时间复杂度。
定理3.1。应用DFS/BFS的时间复杂度为
O |V |×(|VS|+|ES|+|E?|+|V |+|E|) = O(|V |×(|V |+|E|))
证据第3.1条。通过上述的讨论，可以很容易地证明这一点。
由于利用上述技术的高时间复杂度，我们引入了一种新的无知在线搜索策略（UIS，算法1）用于LSCR查询（第3.1节），它可以在g上进行缩放一般标记的图，并为LSCR查询提供了一个基线。之后，我们将讨论如何采用当前的LCR方法的可用性（第3.2节）。

3.1 Baseline of LSCR Queries

算法UIS（G，Q）首先将一个元素s输入堆栈S（第1行），并运行到S为空（SL，S9t，第12行）或证明sL，St（第11行）。在UIS中，我们设计了一个函数SCck（v，S）为了验证v是否能满足s。此外，为了管理UIS的召回过程，我们开发了一个超射接近：v→{N，T，F}，如定义3.1所示。
定义3.1。在LSCR查询的搜索算法中，V→{N，T，F}如下： (i)最初，∀u∈V，关闭[u]=N，表示你没有被探索；（ii）如果s L，S通过搜索策略证明了u和s L u，我们分别将[u]在附近设置为T和F。
请注意，这种推测在本文中一直在使用。
将关闭[s]设置为SCck (s、S）（第2行）后，循环（第5行至第11行）从S（第4行）中取一个元素=，并处理每个边标签=（u、l、v）。因此，该算法只有在s到达L下的空间中遍历，即s L u存在。我们在下面的情况下（第6-9行）中探讨v。(1)关闭[u]=T∧关闭[v]=T，意思是sL，su存在。由于u L v和e=（u，l，v）∧l∈L，sL，sv存在，因此接近[v]=T。(2)关闭[u]=T∧关闭[v]=N，其中，如果SCck（v，S）返回true，即v满足S，我们设置关闭[v]=T(否则，我们设置为关闭[v]=F。
分析。为了分析所提出的算法，我们首先在LSCR查询中引入了搜索树。
为了一般考虑，在下面的讨论中，我们假设SCck（s，S）返回false，并且循环（第3-11行）从close[s]=F开始。图4绘制了一个搜索树示例，其中，∀v∈V，我们要区分一下close[v]=T和close[v]=F，用颜色标记它们。

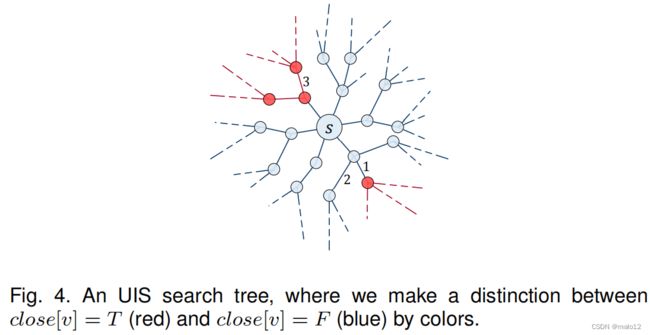
为了说明顶点探索过程，在第6-9行中，我们用数字1、2和3标记了3条边，分别表示e1=（u、l1、v1）、e2=（u、l2、v2）和e3=（u 0、l3、v3）。E1和在情况2中，e2出现，SCck（v1，S）=Strue和SCck（v2，S）=f alse；e3出现，iff，在情况1中，我们探索顶点v3。相比之下，搜索树中的边只能在中生成以上三种方法，因为我们只在案例1和案例2中探索一个顶点。我们在定义3.2中正式定义了搜索树。
定义3.2。一个LSCR查询Q=（s，t，L，S）的搜索树被形式化为T，其中(i)T的根是s；（ii）假设NT表示T的节点集，有一个注入f： V→NT和，∀u∈V，u在NT中最多指向两个节点vF和vT；（iii）vF（接近[v]=F）和vT（接近[v]=T）表示当顶点v被搜索算法传递时，v在接近时的状态。
最后，我们分别在定理3.2和3.3中证明了算法的正确性和时间复杂度。
定理3.2。（算法1的正确性。）Q是一个true查询，iff，UIS（G，Q）返回true。
证据3.2。（⇒）Q是一个真正的查询，iff，∃p∈P（s，t）∧∃v∈∈和v满足子结构约束。假设p=<，e0，…，v，…，ek，t >和v是p中的第一个顶点，其中sLv，v L t和close[v]=T存在。由于UIS具有回忆一个顶点w的能力，其中w的接近状态为F，因此该语句是明显有效的。（⇐）如果UIS返回true，则Tu中存在一个节点vtssLst和Q是一个真正的查询。
定理3.3。UIS（G，Q）的时间复杂度为O(|VS|+|ES|+|E?|) + |E|,S=（？x，VS，ES，E？）
证据3.3。函数SCck（v，S）的时间复杂度为O（|VS|+|ES|+|E？|）。我们调用这样的函数高达|V |时间。另外，UIS最多可以穿越G两次
定义3.2。因此，UIS遍历G的时间复杂度为O（|V | + |E|）。因此，该陈述被证明了。

3.2 Analysis of LCR Methods

在本节中，我们首先简要回顾一下当前的LCR方法，然后讨论为什么这种方法不能应用到我们的问题上。
评审LCR查询的问题起源于[6]。他们的目的是解决图全传递闭包（TC）预计算中的高空间复杂度问题，并使用一个基于树的索引框架ork.这个框架包含一个生成树（或森林）和一个输入图的部分传递闭包，因此它可以覆盖完整TC的所有信息来响应LCR查询。
[25]将一个输入图分解为几个强连通的分量。对于每个分量，计算一个局部传递闭包，即它们预先计算一个l中每个顶点对的所有CMSs八段传递闭包。然后，它们将每个分量转移到一个二部图中。对于u和v不在同一分量中的顶点对（u，v），从u到v和从v到u ca的两个分量在二部图并集的拓扑顺序中找到。也就是说，不同组件中的顶点的cms也被预先计算出来。因此，预先计算的索引包含了所有的信息of完整的TC。
据我们所知，目前最先进的LCR查询解决方案是[19]。给定一个输入的带边标记图的标签集L，他们首先选择k个地标。对于每个地标顶点v，它们表示将v中的所有CMSs删除到v到达的每个顶点。此外，为了加速LCR查询处理，他们还用b个cms对每个非地标顶点进行索引。另外，让RL (v)={w∈v|vLw}，v是一块土地mark和∀L⊆L，|L|≤|L|/4 + 1，他们为每个地标v预先计算RL (v)，以加速错误查询。
讨论尽管这些技术在回答LCR查询时速度很快，但由于索引时间复杂度非常高，它们不能为索引相对较大的kg进行索引。

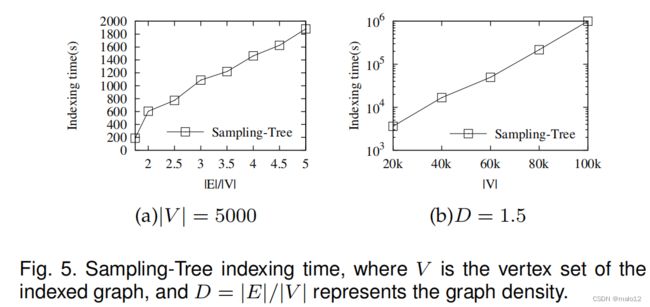
根据[6]的报告（[6]的表1和[6]的表2），生成树的索引时间随着图密度D = |E|/|V |的增加呈线性增加，如图5(a)所示.另外，生成树的索引时间随着|V |的增长而呈指数增长，如图5(b).所示当|V | = 100,000和D = 1.5时，索引时间约为106s≈11.57d。
[25]代表[19]的基线，在[19]中，它们说明[25]在大图上不能伸缩(|V | >5.4k).此外，[19]的索引时间复杂度是Oh非地标顶点。在[19]，k=1250+p |V |和b=20的实验设置中，因此[19]的时间复杂度等于O（|E||V |2 |L| + |V | 22 2|L|）。
因此，对于一个相对较大的图，很难采用上述方法。

4 IMPROVED UNINFORMED SEARCH

对于一个KG G上的LSCR查询Q=（s，t，L，S），UIS必须用函数SCck对每个搜索路径p的每个顶点进行求值，直到∃v∈V §∧v∈V（S，G）存在(v满足子结构约束S).上述操作的时间复杂度很大程度上依赖于给定的子结构约束S. Plus，通过实现LCR查询的技术，UIS无法加速，如第3.2节所述。
由于子结构约束可以被格式化为SPARQL查询（第2节），因此我们可以通过实现SPARQL引擎[1]来获得V（S，G），而不是逐个检查G中的顶点。然后，一个LSCR查询Q可以通过递归验证∃v∈V（S，G），s L v∧v L t的存在来求解。例如，在图3中，V（S0、G0）={v1、v2}。然后，对于一个LSCR查询Q0=(v3，v4，L0={likes，hates，friendOf}，S0)，查询过程可以在验证v3 L v1和v1 L v4的整个序列过程中完成。
因此，在本节中，我们将提出在我们的问题上使用SPARQL引擎的直观想法，称为UIS∗（算法2）。UIS∗的算法分析描述分别在第4.1节和第4.2节中。
请注意，在本文中，我们将V（S，G）中的元素视为无序的，因为现有的（top-k）SPARQL引擎[9]，[23]只能用它们自己的属性对匹配的子图进行排序。

4.1 Algorithm Description

在算法2中，一个全局堆栈S用一个元素s（第1行）初始化，并在整个算法中使用。在3.1定义中引入。请注意，th的定义eUIS∗搜索树与差异3.2相同，在引理4.3中证明了其正确性。
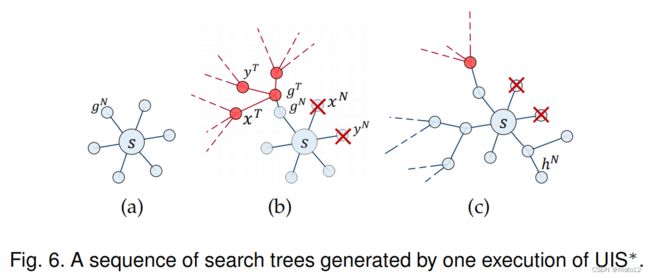
循环（第3-12行）处理每个顶点v∈∗（S，G），用一个函数LCS（s∗，t∗，L，B）（第14-24行）来评估在标签约束下从顶点∗到顶点∗的可达性参数B的值在{T，F}的范围内，其中，如果是s∗∈V（S，G），B=T，否则，B=F。为了清晰起见，我们绘制了两个搜索树序列（g，h∈V（g，S，G）∧g L9 t）h分别如图6和图7所示。
对于一般考虑，假设在UIS∗运行过程中演示s/∈V（S，G）。因此，在循环的第一次迭代中，∀v∈V（S，G），关闭[v]=n。我们在第4-9行中处理v，验证sLv（第6行和第7行）的存在。这样，函数LCS就由参数s∗=、t∗=v、L=L和B=F（s∗=/∈V（S，G））调用。由于B = F，函数LCS只探索顶点w与关闭[w]=N（情况2，第20行），并改变状态在接近F的地方被探索的顶点（第21行）。在下面的说明中，我们通过第一次调用LCS的结果来讨论UIS∗，其中“真”和“假”与s L v和s /Lv，各自地。
s L v.假设v = g，图6(a)描述了第一次调用LCS后的搜索树。在证明了s L g后，我们启动函数LCS，并将参数s∗、t∗、L和B设为g，t，L和T（∈V（∗=，∗=））分别在第8行。然后，使用B=T（s L s∗），我们在s中添加一个元素s∗，并将close[s∗]设置为T（第15行）。然后，对于每条边的e =（u，l，w）用l∈L输出元素u（第18行），我们在情况1（第20行）中另外探索w，并将关闭[w]更改为B（第21行）。
由于实现的数据结构S是一个堆栈，其中元素遵循LIFO（最后入先出）原则，因此首先处理LCS调用中新添加的元素。当然，在LCS的第二次调用中，如果S中的一个元素x并关闭[x]=T，那么s∗Lx，而，如果关闭[x]=F，s∗Lx的存在是未知的。
因此，LCS中的循环运行直到s∗Lt∗被证明，或者∗中第一个元素的状态为F（关闭[st]=∗），其中： (i)在前一种条件下，如s L s∗，s∗∈V（∗，G），s∗Lt∗和∗∗=t都存在，我们在主函数中有s L t。因此，UIS∗停止并返回Q=T（第9行和第12行）。（ii）在后一种情况下，第24行删除了这些元素在这个调用中传递的S中（其接近的状态等于T）。例如，在图6(b)中，元素x和y从S中删除，因为节点xT和节点yT是already在搜索树中。此外，图6©描述了图6(b)可能的一个序列，即h∈V（S，G）。

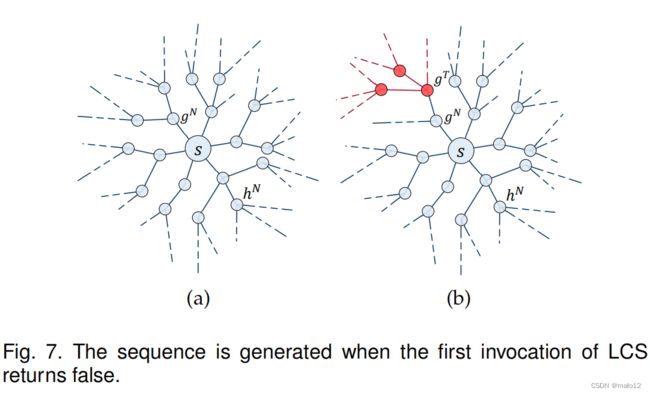
s L9 v.由于B = F，在第一次调用LCS后，∀w∈V，如果s L w，关闭[w]=F，如果s L9 w，关闭[w]=N，堆栈S为空。换句话说，UIS∗已经遍历了所有的顶点ts到达。图7(a)展示了此时UIS∗的搜索树。在稍后的循环迭代（第3-12行）中，只有当关闭[v]=F（第10行）时，我们才评估vLt（第11行）的存在性。这个序列的示意图如图7(b).所示在此基础上，我们给出了一个定理，证明了V（S，G）中元素的处理顺序决定了效率UIS∗。
定理4.1。如果，在使用B = F的LCS的第j次调用中，LCS返回false，那么，在第j次调用之后，∀w∈V∧Lw，关闭[w]=N。
证据第4.1条。我们可以通过上述的讨论来证明这一点。

4.2 Analysis

在本节中，我们分析了UIS∗（G，Q）的正确性和时间复杂度，其中G =（V，E，L，LS）是一个KG，Q=（s，t，L，S）是一个LSCR查询。另外，我们证明了UIS∗的搜索树可以是在引理4.3中形式化为UIS。
引理4.2。假设sLs，∀v∈V，sLv，iff，关闭[v]=N。
证据第4.2条。∀v∈V，closs[v]的值初始化为N，只能在第1行和函数LCS（第14-24行）中更改。因此，在此假设下，我们通过归纳法证明了该陈述e LCS调用时间：
第一次调用。根据算法描述（第4.1节），循环（第17-21行）在此调用中保持与语句相同的循环不变性。k th调用。假设s在（k−1）个调用中是正确的，上面的循环在第k个调用中仍然作为循环不变量：因为s L s∗必须被证明，所以不变量在t之前存在他第一次迭代了这个循环。另外，由于我们只研究了上述两种情况下的顶点，所以在后面的迭代中，不变量是正确的。
然后，引理4.3声明UIS∗（G，Q）的搜索树是在定义3.2中所定义的。
引理4.3。UIS∗的所有搜索路径在一次执行的任何时间都构成一个搜索树T，正如我们在定义3.2中所定义的那样。
证据4.3。这个引理基于引理4.2和定义3.1是有效的。
最后，用定理4.4和4.5分别说明了UIS∗的正确性和时间复杂度。
定理4.4。Q是一个真正的查询，iff，UIS∗返回true。
证据第4.4条。（⇒）如果Q是一个真正的查询，s L，S t。然后，∃p∈P（s，t），L §⊆L和∃u∈V §∧u∈V（s，G）（定理2.1）。假设=<，e0，…，=<，…，>，t>，∃vT在T和TT在Tst.因此，UIS∗返回true。（⇐）如果UIS∗（G，Q）返回true，则T中存在一个同时满足标签约束L和子结构约束s的路径。因此，Q是一个true查询。
定理4.5。UIS∗的时间复杂度为O（|V | + |E|）。
证据：第4.5节。基于引理4.3，UIS∗对G中的每个顶点进行最多处理两次。

5 INFORMED SEARCH

为了解决KGs上的LSCR查询，我们引入了两种不知情的搜索策略：UIS（算法1）和UIS∗（算法2）。前者是LSCR查询的基线方法；后者获得V（S，G）通过实现SPARQL引擎，具有较低的时间复杂度。
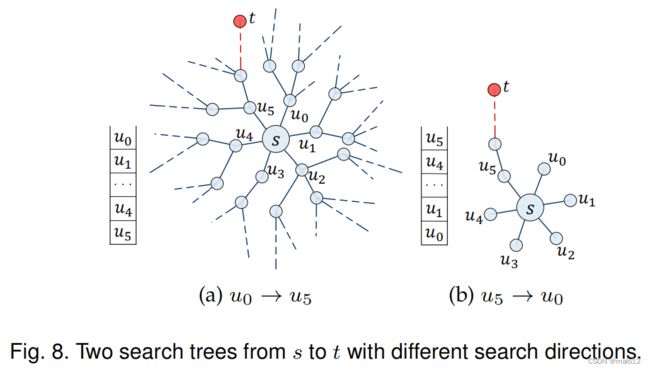
然而，不知情的搜索算法也有它们自己的局限性。它们的查询效率不仅取决于输入KGs的大小（定理3.3和定理4.5），而且还主导了by表示搜索方向（定理4.1)。我们用图8说明了后一种限制，因为上面提出的策略都服从LIFO原则（第3节和第4节）。假设一个顶点s与6个顶点相关联（u0，……，v5，图8），其中只有u5和一个顶点t是可到达的。我们画了两个可能的搜索树从s到t的LIFO算法的LIFO算法。图8(a)中的一个搜索树在查询处理开始时遵循u0→u5的顺序，而图8(b)中的另一个搜索树以u5→u0的顺序开始。显然，上述两个订单的查询效率无法比较。

传统的知情搜索算法[13]，如最佳优先搜索和A*搜索，用一个评估（启发式）函数来探索输入图。有了这样的功能，就有了一种知情的搜索方法可以打破LIFO和FIFO原则的固定搜索顺序，并可以找到一个相对较短的搜索路径来提高查询效率。不幸的是，上述知情的搜索策略不召回，这类似于DFS/BFS（第3节）。此外，上述技术的评估函数过于简单，无法扩展到kg上的复杂的LSCR查询。
受传统知情搜索技术的启发，在本节中，我们提出了一种LSCR上LSCR查询的知情搜索算法，名为INS。该算法类似于UIS∗，除了fol降低两点。首先，它在第5.1节中使用了一个轻量级索引（本地索引），在一个有限的索引时间复杂度内减少了在线计算消耗。第二，INS应用程序的两个数据结构（第5.2节），优先级堆H和优先级队列Q，以实现在传统的知情策略中的评估功能。

5.1 Indexing Strategy

我们在KG G=（V，E，L，LS）上的局部索引的直觉想法类似于地标索引[19]（第3.2节）。不同之处在于，我们可以通过预先计算来限制索引时间复杂度ng在G的特定子图中选择每个地标，而不是在整个输入KG中。
在下面的部分中，我们将概述第5.1.1节中的索引技术，其中将正式定义了本地索引。然后，对该索引策略进行了算法描述 5.1.2，然后进行正确性和复杂性分析。

5.1.1 Overview

本概述从说明[19]和本地索引之间的区别开始，并通过一个示例（图9），然后介绍了本地索引的正式定义。
根据第3.2节中对[19]的描述，我们将传统的地标索引形式化为叠加f：I→{G}，其中I表示所选对象的集合地标（最高度）和{G}表示I中地标的索引范围。例如，在图9(a)中，I={图9(a)中突出显示的顶点}，以及，对于I中的每个顶点v，[19]pre计算图9(a).中从v到任何其他顶点的CMSs显然，当G的大小增长时，这种方法的索引时间呈指数增长，正如我们在3.2节中讨论的。

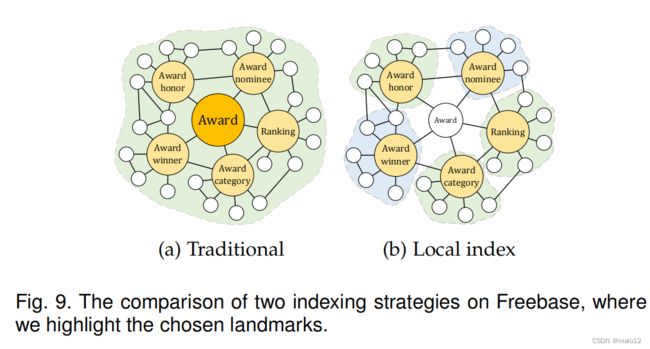
为了克服无界索引时间复杂度，我们的目标是将每个选择的地标的预先计算范围从整个G缩小到一个子图，如图9(b).所示对于正式的描述离子，一个双射F：I→G存在于我们的索引策略（算法3）中，其中I是所选地标的集合，对于一个地标u∈I，F (u)∈G是地标u所属的子图。重要的是，对于F (u)中的每个非地标顶点v，我们规定顶点u到达顶点v，并且，对于一个子图F (u)∈G，u是唯一一个被选择的地标。另外，这是结合的结果G中的所有子图并不一定包含G中的所有元素。
定义。局部索引中的一个条目与I中的一个地标u相关，并由II[u]∪EIT[u]∪D[u]形式化。在介绍关于这类条目的细节之前，我们将介绍一些本地索引-rela了定义。假设Gu=F (u)是G的一个子图，则其顶点集和边集分别用Vu和Eu表示。首先，一个路径集P（s，t|Gu）是P（s，t）的一个子集，其中，∀p∈P（s，t|Gu），对于p，∈∈中的每条边。然后，我们将M（s，t|Gu）定义如下。
定义5.1。标签集的集合M（年代，t|顾）是一个CMS从年代到t在一个子图的顾G，如果M(s, t|Gu) ={L(pi)|pi ∈ P(s, t|Gu) ∧ @ pj ∈ P(s, t|Gu), i = j, L(pj ) ⊂ L(pi)}.
然后，假设Eo = {（v，l，w）|v∈Vu∧w/∈Vu}是G的一个边集，其中Eo中的每条边都指向F (u)中的一个顶点，并指向一个不在F (u)中的顶点，我们定义两组=(顶点，标签集的集合）键值对，II[u]和EI[u]。前II[u] = {（v，M（u，v|F (u)））|v∈Vu}和后者EI[u] =（w，L）|∃（v，l，w）∈Eo，L = {L∪l|L∈M（u，v|F (u)）}。
在II[u]中的成对的意义是显而易见的。对于EI[u]中的一对（w，L），存在以下语句：给定一个标签约束L，如果是∃Lw∈L和Lw⊆L，则u L w。这一点很容易被证明EI的定义。为了查询效率的要求，在实践中，我们对EI[u]中的对进行反转，并将它们恢复为EIT [u]中的（标签集，顶点集）键值对，其中EIT[u]=∀(L, V)|∃(w, Lw) ∈ EI[u] ∧ L∈Lw, V={v|∀(v, Lv)∈EI[u] ∧ L∈Lv} .在这里，我们在定理5.1中进一步讨论EIT。
定理5.1。如果Lu⊆L，则∀v∈Vu，u L v，其中（Lu，Vu）是EIT [u]中的一对，L是一个标签约束。
证明书第5.1节。EIT [u]中的∀（Lu，Vu），对于Vu中的每个顶点w，在EI[u]中必须有一个Lu∈L，∈)。如果是Lu⊆L∧Lu∈L，那么u L w。
最后，为了给出G中两个子图F (u)和F (v)之间的相关度的初步估计，我们发展了D[u]={（v，D（u，v）|v∈I）}，其中D（u，v）是中的对（w，L）的数量其第一个元素w是F (v)中的一个顶点。

5.1.2 Algorithm Description

在这一部分中，我们介绍了双射F和局部指数项II[u]∪EIT [u]∪D[u]的构造过程的算法3。
INS中的地标选择过程比[19]中更为复杂，其中[19]直接选择程度最高的顶点。根据第2节中对KGs的描述，e许多真实世界实例的ntiis通常与KG中度相对较高的顶点相关，如图2所示。另外，指向或指向这些顶点的边通常是实验的由一组RDF词汇表组成，例如。“rdf：type”，“rdfs：子类”。选择具有最高度的顶点将导致地标和非陆地之间的关联边的标签简单一点。换句话说，当输入标签约束不包含任何RDF词汇表时，基于这些地标的本地索引是无用的。
为了选择一组强健的地标(I)，INS的地标选择过程（第1行）基于输入KG G的RDF模式LS，首先在LS中随机选择一组类，然后均匀标记所选类的k个实例作为地标性建筑(I)。由于|I|越小，在查询处理中遇到地标的机会就越小，在INS中，我们设置了|I| = k = log |V |×p|V|。
在此之后，为了构造F（第2行），我们从I中的所有顶点启动一个BFS（函数BFS，第26-34行），同时遍历它们周围的顶点，使用以下规则：对于edge e =（v，l，w）∈=，如果v和w都属于子图F (u)，则=是F (u)的一条边。考虑到有效搜索顶点ww的子图的实际要求到，我们为G中的每个w顶点引入一个额外的属性AF，其中w。AF = u表示顶点w属于子图F(u）（第32行和第12行）。
此外，建议将函数Insert（v，L，index索引[u]）（第16-24行）添加到表示II或EI的指数中，从第16行到第24行。如果@（v，L）∈index[u]，我们添加一个新的pair（v，{L}）到索引[u]（第18-19行）；否则，我们使用（v，L）更新对（v，L）的值，这在第20-24行中得到了演示。
然后，对于I中的每个顶点u，我们在函数LocalFullIndex（u、F）（第3-15行）中索引u，其中II、EI和EIT [u]是空的（键、值）集（第6行)。这个函数利用了一个队列每个元素都是一个（顶点、标签集）对。将第一对（u、{})添加到Q后，循环（第8-14行）开始，并运行到Q为空。这个循环的每次迭代都从Q (Line 9).我们探索与v（第11-14行）相关的边，除了以下情况：（v，L）不能通过函数Insert添加到II[u]（第10行）中。然后，在第11-14行中，对于每条边(v，l，w)，我们将对（w，L∪{l}）加到Q或EI[u]中，这取决于顶点w是否在F (u)中。
最后，我们重新计算EI[u]中的元素，根据它们的定义得到第15行中的EIT [u]和D[u]。
分析。我们研究了算法3在KG G =（V、E、L、LS）上的正确性（定理5.2）和复杂度（定理5.3和定理5.4）。
定理5.2。条目II[u]∪EIT [u]∪D[u]的定义与局部全索引（u，F）的索引结果之间存在一致性。
证据第5.2条。II[u]：对于II[u]中的元素当然是正确的。（⇐）如果，在F (u)，u L v中，那么在F (u)中存在一个路径p，即L§⊆L。如果@ L 0∈L和L0⊆L，则至少有一条通过边不处理功能局部全索引。然而，在这个函数，我们只跳过在已经搜索过从u到那个顶点的所有可能的路径标签集的情况下的顶点。因此，这个假设并不成立。
EIT [u]∪D[u]：基于插入函数插入，EI[u]也存在一致性。因此，关于EITu和Du的陈述是正确的（第15行）。
定理5.3。索引时间复杂度为O(2|L|×(|E|+|V | log 2|L|)
证明5.3。假设，对于一个地标u，F (u)包含n个顶点和m条边。在函数局部全索引(u)中，我们最多将n2个|L的|条目推入队列中。每次推送将花费O (1)个时间a每次调用函数插入需要O（log 2|L|）时间。因此，索引时间复杂度为Pu∈IO (n + m)2|L| + n2|L| log 2|L| ≤O 2|L| × (|E| + |V | log 2|L|)
定理5.4。索引空间复杂性为O |V |2|L| ×(log |V | + |L|)
证据第5.4条。局部索引的每个条目II[u]∪EIT [u]∪D[u]包含O（n2个|L|）元素，假设F (u)包含n个顶点。每个元素的大小为O（log |V | + |L|）。因此，总的指数指数g空间复杂度为Pu∈IO(n2|L|(log |V |+|L|) = O |V |2|L| ×(log |V |+|L|)
与第3.2节中报告的传统地标索引策略[19]的索引时间和空间复杂性相比，我们的局部索引可以约束索引消耗，这是独立的所选地标的数量（|I|）。

5.2 Search Algorithm

为了提供INS（算法4）感知更好的搜索方向的能力，并打破传统的不知情搜索方法的固定搜索方向，我们实现了两个数据str计算方法：一个优先级堆H（第1行）和一个优先级队列Q（第2行）是一个“评估函数”。在引入H和Q的优先级之前，我们让ρ（s，t）表示从顶点s到顶点t的估计距离，其中ρ（s，t）= D (s。AF , t.AF）（第5.1节）。
首先，INS的主要功能与UIS∗从第11行到第14行相似，而在每次循环迭代（第4-14行）中，INS从h中取出顶部元素v。注意，对于两个顶点u，v∈V（S，G），u在H中v的顶部，当： (i)关闭[u]=F，关闭[v]=N；（ii）如果关闭[u]=关闭[v]=F，ρ（u，t）≤ρ（v，t）或u∈I∧v/∈I；（iii）如果关闭[u]=关闭[v]=N，ρ（s，u）≤ρ(s, v) or u ∈ I ∧ v /∈ I;
与UIS∗类似，INS也在整个算法中初始化一个全局变量。我们没有实现一个堆栈，而是使用一个队列Q来增加遇到th的I中的顶点的概率e双射F，因为局部索引覆盖了输入KG G的完整TC（第3.2节）的一部分。即使Q在主函数中用元素s（行2）初始化，其他操作在Q中添加一个元素或从Q中提取一个元素都在函数LCS（s∗，t∗，L，B）中。此外，对于Q中的两个顶点u和v，它存储u在v的前面，当： (i)关闭[u]=T∧close[v]=F；（ii）u. AF = t ∗ .AF = v.AF；（iii）u∈I∧v/∈I；（iv）ρ（u，t∗）≤ρ（v，t∗）；(v)u，v/∈I，关闭[lu]=N∧关闭[lv]=N；（vi）否则，u在v之前被添加到Q中。
注意，对于Q中的两个元素x和y，如果x和y表示G中的同一个顶点，则Q将删除第一个添加的元素。另外，根据上述Q优先级规则，如果关闭[x]=T∧关闭[y]=F，x是inQ中y的前面。然后，在INS中，在具有参数B=T的第k个函数LCS调用中添加到Q中的元素，在这个调用中首先被处理。
在函数LCS（s∗，t∗，L，B）中，对于从Q（第20行）中提取的每个元素u，我们遍历通过一个循环（第21-29行）输入到u的边（e=（u，l，w）∧l∈L）。最初，如果是t∗。AF=w(苏b图F (u)包含顶点t∗)，在第22行中，我们实现了一个函数检查（II[w]，t∗）来评估w L t∗的存在性，其中如果∃（t∗，L）∈II[w]∧∃Li∈L和Li⊆L，函数检查返回true，否则，假的。
然后，在第24行中，如果引入LCS中的两个函数w∈I∈（II[w]）和Push（EIT [w]），并使用预先计算的局部索引II[w]和EIT [w]，以修剪空间，提高查询效率。对于II[w]中的一对（x，L），前者将关闭[x]设置为B，如果关闭[x]=T和∃Li∈L∧Li⊆L；对于EIT [w]中的一对（Lx，V），后者将每个顶点u∈∈添加为Q，如果Lx⊆L∧，则将接近[u]变为BB=T∧关闭[u]=T或Lx⊆L∧B=F∧关闭[u]=N。在此之后，在第26行中，如果w/∈I，我们将w添加到Q中并设置为接近B，如果关闭[w]=N或关闭[w]=F∧B=T，这与UIS∗相同。
分析。我们对一个KG G=（V，E，L，LS）进行了分析，其中查询时间的复杂度和正确性分别在定理5.5和定理5.6中得到了证明。
定理5.5。搜索策略的时间复杂度为O( |E| + |V | × (log |V | + 2|L|)
证据第5.5条。局部索引中的每个条目II[u]∪EIT[u]∪D[u]都包含O（n2 L）元素，假设F (u)包含n个顶点。在最坏的情况下，我们在一个查询处理s中访问I的所有地标O表示总局部指数访问时间复杂度为O（|V |2 L）。我们最多只遍历输入的KG G两次。因此，遍历时间复杂度的图为O（|V | + |E|）。此外，我们执行一个组合对Q中|V |元素的排序，但上述操作只能发生一次，因此其时间复杂度为O（|V | log |V |）。总的来说，总复杂度为O（|E| + |V |×（log |V | + 2|L|））。
定理5.6。Q是一个真查询，iff，INS返回true。
证据第5.6条。INS与UIS∗在以下方面的不同： (i) INS利用算法3约束的局部索引；（ii）INS以顺序处理V（S、G）中的元素；（iii）INS应用具有优先级队列而不是堆栈的全局变量，并且INS不包含在UIS∗的第24行中的操作。根据定理5.2，(i)和（ii）都不影响其正确性的INS。然后，全局变量可以自动删除重复的元素，并将超投影中值接近的元素的T保持在队列的前面。因此，INS仍然持有t他的正确性。

6 EXPERIMENTAL RESULTS

在本节中，我们将评估所提出的算法：UIS，UIS∗和INS，在合成的和真实的KGs上的性能。特别是，由于标签约束对查询性能的影响nce已被广泛研究，[6]，[19]，在本节中，我们感兴趣的是：我们的本地索引的索引时间和空间消耗；KG尺度对查询性能的影响；子结构约束对查询效率的影响，包括子结构约束的选择性和能够满足子结构约束的顶点的数量。
在介绍了实验评价中的设置和措施后，我们分别在6.1节和6.2节中详细说明了在合成数据集和真实数据集上的实验.此外，基于所有的实验结果，我们在第6.3节中进行了讨论。
设置我们的实验运行在一台具有intel i7-9700 CPU、64 GB RAM和1TB磁盘空间的机器上。本文用Java实现了本文中提出的所有算法。另外，为了避免th的影响e实现语言中，传统的地标索引方法[19]也用Java实现，[19]的索引参数k和b分别设置为1250+p |V |和20在[19]的实验中。请注意，由本地索引和[19]构建的索引由相同的数据结构并存储在磁盘上。
然后，我们利用[20]中存在的UIS∗和INS的SPARQL引擎，它也用Java重写。SPARQL发动机的采用是由于它在实验中的高效率l.本文的设置。因为这为查询结果提供了对参数的控制UNIMax，M ax和Eδ，为了获得完整的V（S，G）集合，根据[20]，我们将参数UNIMax和M ax设为+∞，并将Eδ设为1。
此外，本实验中使用的数据集是利哈伊大学基准（LUBM）[4]和YAGO [18]。前者是一个基于大学领域本体论的综合基准提供可伸缩的合成数据生成器；后者是一个巨大的语义KG，源自维基百科、WordNet等，包含约1000万个实体和1.2亿个事实。
查询性能度量。对于以下实验中的一组评估查询，查询性能的度量包括： (i)查询的平均运行时间；（ii）av前一种度量的原因是显而易见的，而我们使用后者，而不是搜索树T中的节点数（|T|），是因为|T|可以直接反映。

6.1 Experiments on LUBM

我们通过应用LUBM随机生成数据集D0-D5（表2）。即使D0包含40k顶点和230k边，并且只用于比较局部索引和t的索引消耗他传统的地标索引[19]，其规模仍然大大超过了在[6]，[19]中使用的大多数数据集。在D0-D5的基础上，我们评估了两个局部区域的索引时间和空间消耗dex和传统的地标索引方法[19]。结果如表2所示，这证实了我们的理论分析，与[19]相比，我们的本地ind的索引消耗交货价是可以负担得起的，而且还在与输入的KG比例尺呈线性增加关系。请注意，索引过程被限制在8小时内。

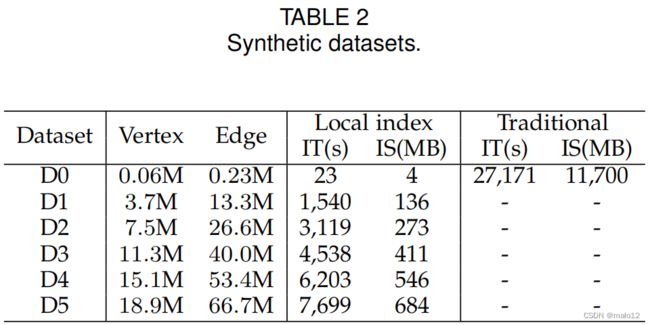
之后，我们进行了一组实验，每一组都与S1- S5中一定的子结构约束有关（用SPARQL，表3表示），并在D1-D5上运行。原因是，为什么我们不反对在LUBM [4]中提供的查询是，它们是为评估RDF引擎查询优化器和概念推理[14]的性能而设计的，并且对我们的评估是无用的。

在介绍了S1-S5的特性后，我们分别在第6.1.1节和第6.1.2节中演示了上述各组的查询生成方法和实验结果分析。假设D是由LUBM生成的数据集，其顶点集为V。S1是一个简单的顶点，它只匹配其研究兴趣是“研究12”的顶点。我们将s1视为我们的子结构约束基线在S1-S5之间，其中|V（S1，D）| |V |≈1‰。与S1相比，S2包含一个正常的选择性，它与也应该是副教授的顶点相匹配，而|V（S2，D）||V（S1，D）|≈为50%。Then，我们设计了S3，其中|V（S3，D）||V（S1，D）|≈120，这意味着在D中有大量的顶点可以满足S3。然后，S4与高选择性和|V（S4，D）||V（S1，D）|≈1有关，其中t他在|V（S4，D）|中的顶点被命名为“毕业学生4”，参加一门课程？y1，等等。特别是|V（S5，D）|=1。

6.1.1 Evaluation query generation

在我们的实验中，生成一个评估查询Q=（s，t，L，S）是复杂的，因为如果s只需几步就达到t，Q不能检验搜索算法的局限性。另外，由于这个存在由于影响查询性能的不相关因素，我们必须确保我们的实验不受这些不相关因素。
控制无关变量的方法。显然，标签约束是影响查询效率的主要因素之一，但我们在实验中没有关注这一点，因为影响在LCR的工作中，对查询效率的标签约束进行了广泛的研究。假设t是输入KG标签集的大小，对于每一组查询，我们保证标签c的大小约束范围在[0.2t、0.8t]范围内，确保这些尺寸在[0.2t、0.4t)、[0.4t、0.6t)和[0.6t、0.8t]范围内均匀分布。此外，对于一组false-LSCR que因此，搜索方法的性能可能会受到错误查询类型的影响。例如，false-LSCR查询Q（L，S9t）有三种可能性：∧t、∧9t和∧9t∧s S9 t.因此，对于生成的错误查询，我们也保证了上述可能性的一致比例。
查询生成方法。对于表3的子结构约束Si和表2的数据集Dj，我们生成了两组LSCR查询：1000个真查询（Qt）和1000个假查询（Qf）。Assuming Q=（s，t，L，Si），这个过程从在Dj上随机选择s和L开始。由于控制不相关变量的限制，如果Q不能添加到Qt或Qf中，我们将重新生成L. T当，为了选择Q的一个声音目标顶点t，我们从s开始一个BFS，并在日志|V |迭代后停止它，之后t是一个BFSun探索的顶点。这是为了过滤掉重存的顶点s只有几个步骤。此外，我们应用UIS来确定Q是否是一个真正的查询（Q=T）（Q=F），以及记录搜索树中的节点数，用|T|表示。在[10 log |V |，|V | 10 log |V | ]中使用随机数min，如果|||

6.1.2 Experimental result analysis

对于与S1相关的LSCR查询的UIS结果，true（图10(a)）和false（图10(b)）查询的平均运行时间均随t的增加呈线性上升趋势他输入KG量表。在这样的查询上，UIS的平均经过顶点数约为106（图10©和图10(d)）。与S1相比，UIS的查询性能，对应于S2(正常selec率)和S4（高选择性），基本保持不变，如图11和图13所示。然而，对于子结构约束S3下的true-LSCR查询（图12），UIS消耗fivE倍的运行时间，与S1相比。另外，S5（图14）对应的真查询和假查询的平均运行时间范围分别为[5s、35s]和[1s、9s]，而平均通过顶点数字仍然在106个左右。这是因为，较大的|V（Si，Dj）|是，较早的UIS在搜索路径中遇到一个顶点v（v∈V（S，G））。这些结果反映了|V（Si，Dj）|在一定程度上影响了UIS的性能。


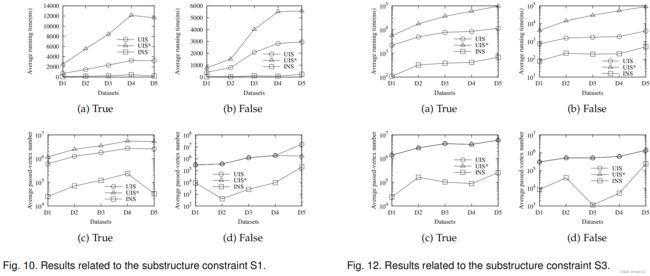
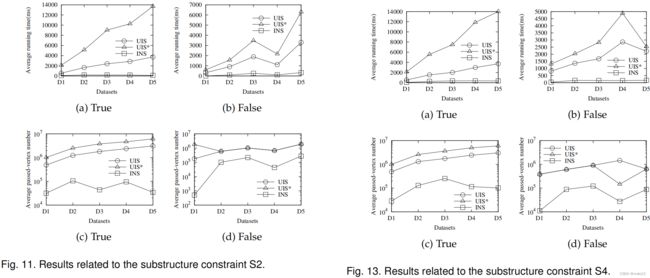
我们观察到，UIS∗和INS的平均运行时间也随着KG规模的增加呈线性增长。具有正常（S2，图11）和高（S4，图13）的子结构约束与S1相比，选择性对UIS∗或INS的查询效率都没有显著影响。此外，根据图12和图14所示的结果，verti的数量满足给定子结构约束的输入KG中的ces也会影响UIS∗和INS的查询性能。那么，尽管UIS∗是UIS的改进算法，但UI的性能S∗对实际查询并不令人满意，UIS∗的线性增长斜率大于UIS，但S5除外（图14）。这是因为V中顶点的顺序，G)是随机的，导致UIS∗总是陷入一个不好的方向。结果显示在图12和图14中表明，不良方向（定理4.1）的影响远远大于高选择性的影响。但是，使用局部索引来修剪搜索空间和s根据图10-14中报告的实验结果，INS选择了更好的搜索方向，克服了UIS∗的上述缺点，获得了比UIS和UIS∗更高的效率。

6.2 Experiments on YAGO

所利用的数据集YAGO1包括大约4M个顶点和13M条边。YAGO上局部索引的索引时间和空间消耗分别为4993s和86MB。
评估查询生成。我们在真实的KG YAGO（用G表示）上开发了一组实验。每一组实验还对应于两组LSCR查询：1000个真查询（Qt）以及1000个错误序列（Qf）。与在LUBM上不同的是，我们随机生成Qt和Qf的子结构约束，其中在G上满足这种约束的顶点数为in相同的数量级m（m∈{101,102，…}）。
Qt和Qf的测试查询生成过程如下。首先，假设Q=（s，t，L，S），同时得到s，t和L的方法，以及控制无关变量的方法如第6.1.1节所示。然后，对于G的子结构约束S，我们让|V（S，G）|在[0.8m，1.2m]的范围内，并随机在G中选择一个实例顶点v（第2节）。根据对于G的RDF模式和与v相关的边，我们初始化了S=（？x、VS、ES、E？）选择性较小，其中v∈V（S，G）。然后，根据|V（S，G）|与[0.8m，1之间的差距，我们逐步随机调整VS、ES和E？。最后，Q是属于Qt，还是属于Qf，还是我们丢弃Q，也如第6.1.1节所示。
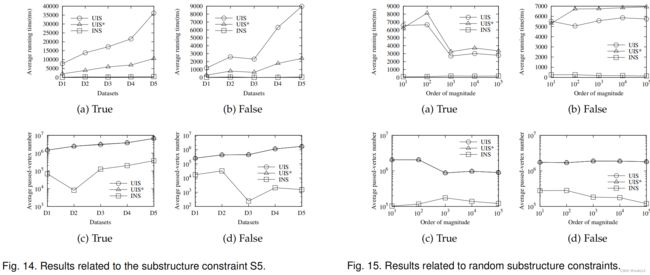
实验结果分析。上述实验的结果如图15所示。假设Q（r，m）表示一组求值查询，其中： (i) if r = T，Q（r，m）中的每个查询都为true，否则为false；（ii）m表示如上所述的数量级。UIS的平均运行时间与Q (T，1上的实验相比呈下降趋势01)（约7秒）到Q（T，105）（约3秒），如图15(a).所示对于错误的查询（图15(b)），UIS的平均运行时间从Q（F，101）到Q (F，105 )，大约稳定在5.5s。此外，根据图15©- 15(d).，其平均传递顶点数的变化趋势与平均运行时间相似
UIS∗的查询性能仍然低于UIS，特别是在与错误查询相关的实验中（图15©），而UIS∗的传递数几乎等于U“是的。。这些结果进一步证明了UIS∗在输入KG中重复遍历顶点的比例更高。通过局部索引修剪搜索空间，加速查询处理，在整个实验过程中，INS的性能是最好的。在true-LSCR和false-LSCR查询上，INS的平均在线搜索时间消耗约为UIS或UIS∗的千分之一.
然而，上述结果似乎与第6.1节不同，在第6.1节中，|V（S，G）|高度主导了LSCR查询Q=（s，t，L，S）的查询效率。这是因为潜在的s随机生成的评估查询的arch空间受到m的影响： (i)对于一组真实查询Q（T，m），更大的m表示输入KG中满足随机生成的s的维格更多子结构约束，使得从一个顶点到另一个顶点的搜索相对容易，因此效率略有提高；（ii）对于一组错误查询Q（F，m），作为搜索算法在给定的子结构约束下，在一个顶点s到达的空间中运行，其中每个顶点最多可以遍历两次，效率几乎不受m的影响。

6.3 Discussion

对于第6.1节和第6.2节中显示的实验结果，我们观察到： (i)与[19]相比，[19]索引时间和空间消耗是负担得起的；（ii）与UIS和UIS∗相比，INS在输入KG的不同尺度上取得了良好的性能，即使在一个大的KG上，不同的d三种算法都存在查询性能下降的问题；（iii）子结构约束S的选择性对所提出的三种算法的查询性能影响不大，在LSCR查询Q=（s，t，L，S）上，而|V（S，G）|是主导查询效率的主要因素。

7 CONCLUSION

本文介绍了在KGs上的可达性问题的一个新变体，即LSCR查询，它包含标签和子结构约束。对kg的LSCR查询要复杂得多n现有的可达性查询，它只考虑标签约束。一方面，应用传统在线搜索策略（DFS/BFS）的查询处理时间复杂度则不能提供。另一方面，使用LCR查询技术索引一个相对较大的KG是不现实的，因为索引时间随着输入KG的规模呈指数级增长。这项工作首先进行不仅在kg上，而且在一般图上为LSCR查询的基线方法（UIS）。然后，在介绍了实现SPARQL引擎来解决我们的问题的直觉想法之后，我们设计了一种具有局部索引的知情搜索算法INS。我们对合成数据集和真实数据集的实验评估证实了局部索引的时间和空间消耗是可承受的基于本地索引，INS有效地解决了KGs上的LSCR查询。