《Poluparity Prediction on Social Platforms with Coupled Graph Neural Networks》阅读笔记

论文地址：Popularity Prediction on Social Platforms with Coupled Graph Neural Networks

文章概览

作者提出了一种耦合图神经网络（Coupled Graph Neural Network, Coupled GNN）模型来进行在线内容流行度的预测，该模型包含两个GNN，即State GNN和Influence GNN。其中，State GNN通过用户的激活状态来建模人际影响，而Influence GNN通过来自邻居的人际影响来建模用户的激活状态。

图1: 耦合GNN结构

问题定义

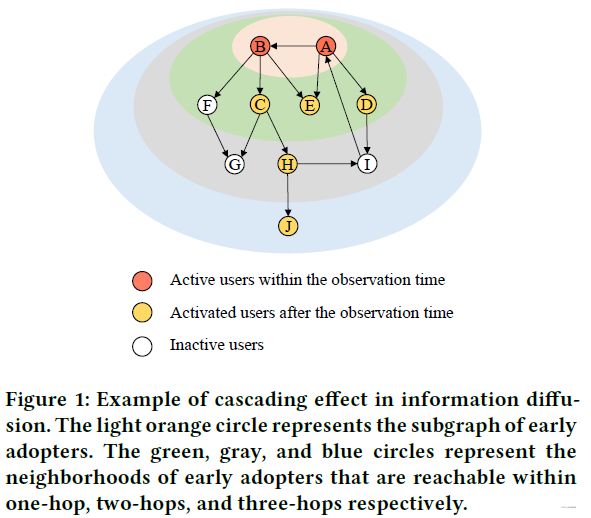
假设有$M$条信息，信息 $m$ 的观察级联被记录为观察时间窗口$T$内的早期采用者集合，即$C_T^m=\{u_1,u_2,...,u_{n_T^m}\}$，其中$n_T^m$表示信息$m$在观察时间窗口$T$内采用或活跃的用户总数。例如下图中$C_T^m=\{A,B\}$。

图2：级联影响的示例

给定观察级联$C_T^m$和底层网络$\mathcal{G}=(\mathcal{V},\mathcal{E})$，其中$\mathcal{V}$为用户集，$\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ 是所有用户之间的关系集，本文的目标为预测信息$m$最终的流行度，例如$n_{\infty }^m$。

模型详解

Coupled GNN的结构参见图1，可以看出State GNN和Influence GNN中结点的消息聚合和更新是相互耦合的，其中State GNN中传递的消息为人际影响，而Influence GNN中传递的消息为用户状态。

State GNN

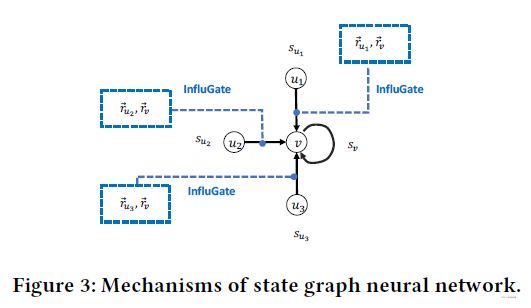
对于目标用户$v\notin C_T^m$，由于他会被其邻居$\mathcal{N}(v)$中活跃用户所影响，作者使用一个GNN来建模用户的激活状态。State GNN的机制如图3所示，其中$r_u$表示的是用户$u$的影响力表示，可以看出某个用户$v$的激活状态需要受自身和邻居的影响力和自身激活状态的影响。

图3: State GNN的机制

State GNN的数学形式如下所示：
$$\begin{gathered} \text{InfluGate}(r_u^{(k)},r_v^{(k)})={\beta }^{(k)}[W^{(k)}{r}_u^{(k)}||W^{(k)}{r}_v^{(k)}] \\ {a}_v^{(k)}=\sum _{u\in \mathcal{N}(v)}\text{InfluGate}(r_u^{(k)},r_v^{(k)})s_u^{(k)}+p_v \\ {s}_v^{(k+1)}=\{\begin{array}{l}1,v\in C_T^m\\ \sigma ({\mu }_s^{(k)}{s}_v^{(k)}+{\mu }_a^{(k)}{a}_v^{(k)}),v\notin C_T^m\end{array} \end{gathered}$$
其中$r_u^{(k)}\in {\mathbb{R}}^{h^{(k)}}$表示第$k$层的影响力表示，$W^{(k)}\in {\mathbb{R}}^{h^{(k+1)}\times h^{(k)}}$是将影响力表示从$h^{(k)}$维转换为$h^{(k+1)}$维的权重矩阵，${\beta }^{(}k)\in {\mathbb{R}}^{2h^{(k+1)}}$是一个权重向量，$s_v^{(k)}$表示用户$v$上一个激活状态，${\mu }_s^{(k)},{\mu }_a^{(k)}\in \mathbb{R}$表示权重参数，$\sigma$表示非线性激活，$p_v\in \mathbb{R}$是一个激活参数，它反映的是用户不被跟随关系影响但被激活的概率。

公式中$a_v^{(k)}$的计算公式表示的是State GNN的消息聚合，而$s_v^{(k+1)}$表示的是结点的消息更新。

注：

• 图$\mathcal{G}$中的任意用户$v$，当其属于$C_T^m$时，其$s_v^{(0)}$为1，否则为0；
• $||$表示concatenation，即拼接操作。

Influence GNN

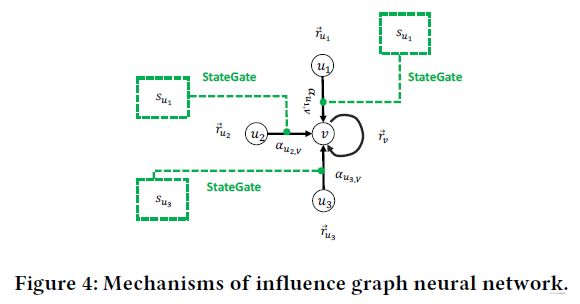
Influence GNN用来建模社交网络中的人际影响的扩散。与State GNN类似，每个用户的影响力表示受自身激活状态和邻居激活状态以及自身影响力的影响。Influence GNN的机制如图4所示，其中$s_u$表示的是用户$u$的激活状态。

图4: Influence GNN的机制

其用公式可以表示为：
$$\begin{gathered} b_v^{(k)}=\sum _{u\in \mathcal{N}(v)}\text{StateGate}(s_u^{(k)}){\alpha }_{uv}^{(k)}{W}^{(k)}{r}_u^{(k)} \\ {e}_{uv}^{(k)}={\gamma }^{(k)}[W^{(k)}{r}_u^{(k)}||W^{(k)}{r}_v^{(k)}] \\ {\alpha }_{uv}=\text{softmax}(e_{uv}^{(k)})=\frac{\text{exp}(e_{uv}^{(k)})}{{\sum }_{z\in \mathcal{N}(v)}\text{exp}(e_{zv}^{(k)})} \\ {r}_v^{(k+1)}=\sigma ({\zeta }_r^{(k)}{W}^{(k)}{r}_v^{(k)}+{\zeta }_b^{(k)}{b}_v^{(k)}) \end{gathered}$$
其中$W^{(k)}\in {\mathbb{R}}^{h^{(k+1)}\times h^{(k)}}$是一个权重矩阵，用来将影响力表示从$h^{(k)}$到$h^{(k+1)}$，${\alpha }_{uv}^{(k)}$为用户$u$到用户$v$的注意力权重，${\gamma }^{(k)}\in {\mathbb{R}}^{2h^{(k)}}$也是一个权重向量，${\zeta }_r^{(k)},{\zeta }_b^{(k)}\in \mathbb{R}$是权重参数。

注：用户$v$的初始化影响力$r_v^{(0)}$由结点嵌入和结点特征构成。

输出层

经过$K$层GNN后的每个用户输出的激活概率分布为$s_v^{(K)}\in [0,1]$，而流行度则通过求和池化机制（sum pooling mechanism）来计算：
$${\hat{n}}_{\infty }^m=\sum _{\mu \in \mathcal{V}}{s}_u^{(K)}$$
在优化的过程中，作者使用的损失函数为$L$:
$$\begin{gathered} L=L_{MRSE}+L_{Reg} \\ {L}_{MRSE}=\frac{1}{M}\sum _{m=1}^M(\frac{{\hat{n}}_{\infty }^m-n_{\infty }^m}{n_{\infty }^m}{)}^2 \\ L=\eta \sum _{p\in \mathcal{P}}||P|{|}_2+\lambda L_{user} \end{gathered}$$
其中$\mathcal{P}$为参数集合，$\eta$和$\lambda$为超级参数，$L_{user}$为用户级别的交叉熵，例如：
$$L_{user}=\frac{1}{M}\sum _{m=1}^M\frac{1}{\mathcal{V}}\sum _{v\in \mathcal{V}}(s_v^{\infty }\text{log}{s}_v^{(K)}+(1-s_v^{\infty })\text{log}{s}_v^{(K)})$$
其中$s_v^{\infty }$为每个用户真实的最终激活状态。

实验

数据集

作者使用了两个数据集，一个人工生成的数据集（Synthetic Dataset）和新浪微博数据集（Sina Weibo Dataset）。其中Synthectic Dataset对应的网络结构包含了1086个结点和4038条边，至于信息的级联传播，作者是先采样种子集，然后用扩散算法（IC Model）来获取信息扩展后各结点的状态，最终总共有27218条信息的扩散结果，观察时间窗口为2个时间步。

而新浪微博数据集则是真实世界中收集的，该数据集的网络为一个跟随网络（following network），作者使用的网络包含23681个用户和1802146条边，其中有3228条信息的扩散结果，作者设置了3个不同的观察时间窗口，即1小时、2小时和3小时。

实验结果

作者使用了MRSE（Mean Relative Square Error）、mRSE（Median Relative Square Error）、MAPE（Mean Absolute Percentage Error ）和WroPerc（Wrong Percentage Error）四个指标来评估算法的性能。

注：这些指标值越小模型的性能越好。

首先作者展示了CoupledGNN一众baseline的对比结果，结果参见表1和表2，可以看出CoupledGNN的性能处于SOTA地位。

为了验证耦合GNN模型的有效性，作者单独使用GCN和GAT来进行激活状态和影响力的传递、更新与聚合，结果展示在表3中，从表3可以看出，仅使用单独的GNN的效果的却比不上使用耦合GNN的，由此验证了耦合设计是有用的。

结语

若有不对的地方请批评指正！！！