论文笔记:www2019 层次图视角的半监督图分类
Semi-Supervised Graph Classification: A Hierarchical GraphPerspective(层次图视角的半监督图分类)是层次图提出的第一篇文章,也是我组会讲的第一篇文章,整理了我的笔记,对论文中的SAGE模块做了比较详细的介绍
- 模型概述
- 损失函数
- SAGE模块(Self Attention Graph Embedding)
- 算法描述与解释
- 实验
- 参考文献
模型概述
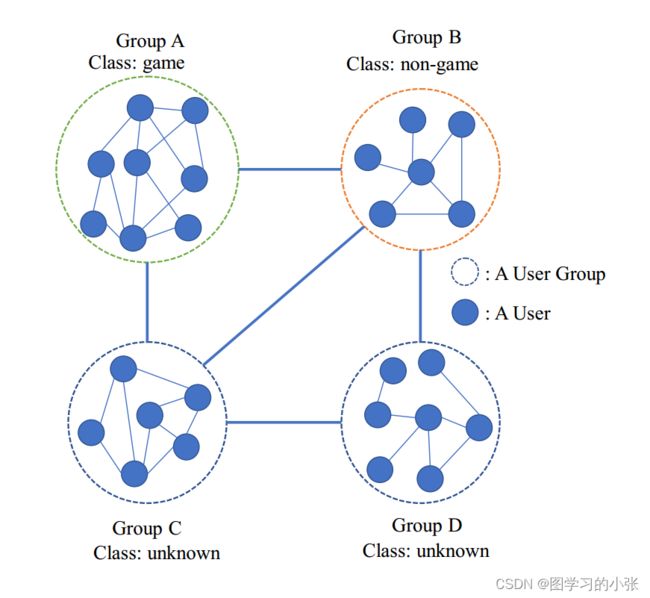
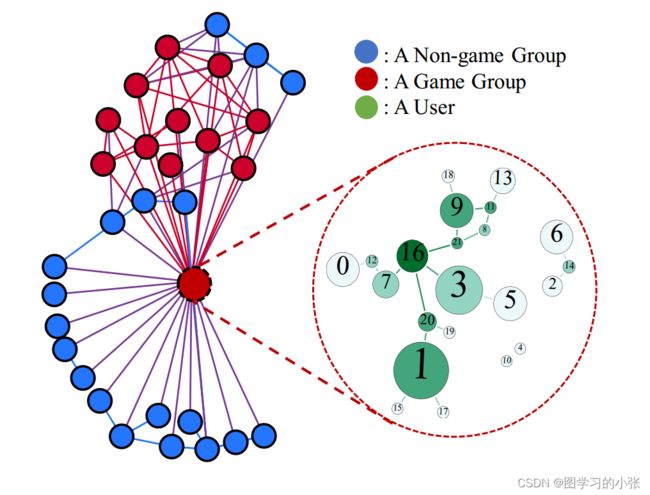
所谓层次图指的是A node itself is a graph instance,即图节点本身也是一个图实例,简单地说,就是大图包小图。图1是论文给出的在社交网络中的
这种结构是非常实用的,举例来说,在社交网络领域,可以通过用户群组之间的关系可以建立一张图,群中的群成员之间的关系也可以建为一张图,这样就构成了一个层次图结构,图1是论文给出的社交网络中的例子,其中,每个图实例表示一个用户群组;在文本识别的领域,也可以把文章与文章之间建立一张图,文章里面里面的word建立一张图,构成一个层次图结构。

损失函数
首先本文进行的是一个半监督任务,模型的损失函数就分为两部分:一部分是label样本的损失,一部分是unlabel样本的损失。
m i n ζ ( G l ) + ξ ( G u ) (1) min\ \zeta(G_l)+\xi(G_u)\tag1 min ζ(Gl)+ξ(Gu)(1) 其中, ζ ( G l ) \zeta(G_l) ζ(Gl)是label样本的损失,其计算公式为:
ζ ( G l ) = ∑ g i ∈ G l ( Γ ( y i , ψ i ) , Γ ( y i , γ i ) ) (2) \zeta(G_l)=\sum_{g_i\in G_l}(\Gamma(y_i,\psi_i),\Gamma(y_i,\gamma_i))\tag2 ζ(Gl)=gi∈Gl∑(Γ(yi,ψi),Γ(yi,γi))(2) 其中, ψ i \psi_i ψi是IC的预测结果, γ i \gamma_i γi是HC的预测结果, y i y_i yi是图实例的标签, Γ \Gamma Γ是交叉熵。
ξ ( G u ) \xi(G_u) ξ(Gu)是unlabel的样本的损失,其计算公式为:
ζ ( G u ) = ∑ g i ∈ G l D K L ( ψ i ∣ ∣ γ i ) (3) \zeta(G_u)=\sum_{g_i\in G_l}D_{KL}(\psi_i||\gamma_i)\tag3 ζ(Gu)=gi∈Gl∑DKL(ψi∣∣γi)(3) 对于unlabel的样本,计算的损失是IC和HC对该图实例预测结果的散度,两个分类器预测结果的偏差越小,损失就越小,文章认为这样的预测结果是更精确的。
SAGE模块(Self Attention Graph Embedding)
根据前面的讲解,我们需要在IC对图实例进行分类的同时,把这个图实例转为一个图的嵌入表示(graph embedding),文章提出了一种Self Attention Graph Embedding (SACE)的方法完成这个任务,在设计SAGE之前,文章提出了解决该问题的三个要点:

第一个是尺寸不变性,就是怎么把大小不同的图构建成一个固定长度的embeding。第二个是平移不变性,就是这个图实例中节点的顺序对于构建的embeding应该是没有影响的,因为节点是没有顺序的。第三个是节点重要性。就是图实例中不同节点的重要性可能有区别(例如QQ群的群主),考虑怎么把不同节点的重要性编码到我们得到的的嵌入表示里。
在这个任务中,我们的输入是一个图实例的邻接矩阵 A ∈ R n × n A\in R^{n×n} A∈Rn×n,特征矩阵 X ∈ R n × ϕ X\in R^{n×\phi} X∈Rn×ϕ,输出是一个固定长度的特征向量,SAGE的结构:
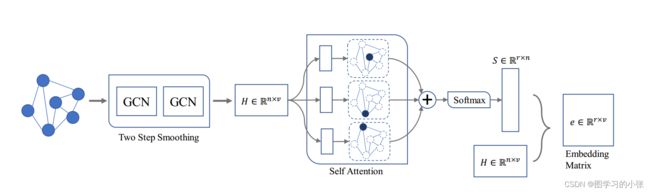
A ^ = D ~ − 1 2 ( A + I n ) D ~ − 1 2 (4) \hat A=\tilde{D}^{-\frac 12} (A+I_n)\tilde{D}^{-\frac 12}\tag4 A^=D~−21(A+In)D~−21(4) 经过两层GCN的传播过程: H = A ^ R e l u ( A ^ X W 0 ) W 1 (5) H=\hat ARelu(\hat AXW^0)W^1\tag5 H=A^Relu(A^XW0)W1(5) 得到一个传播后的矩阵 H ∈ R n × v H\in R^{n×v} H∈Rn×v。这里得到的 H H H不提供节点重要性,而且它是大小可变的,即它的大小仍然由节点数量n决定。所以接下来本文利用自关注机制来学习节点重要性,并将其编码为一个统一的图表示,这个图表示是大小不变的:
S = s o f t m a x ( W s 2 t a n h ( W s 1 H T ) ) (6) S=softmax(W_{s2}tanh(W_s1H^T))\tag6 S=softmax(Ws2tanh(Ws1HT))(6) W s 1 ∈ R d × v W_{s1}\in R^{d×v} Ws1∈Rd×v和 W s 2 ∈ R r × d W_{s2}\in R^{r×d} Ws2∈Rr×d是两个权重矩阵, W s 1 W_{s1} Ws1将将节点表示线性变换到d维空间,然后与tanh激活函数结合引入非线性, W s 2 W_{s2} Ws2则是推断图中每个节点重要性的r个视图。这就像邀请r个专家对每个节点的重要性发表他们的意见。然后应用softmax导出图中每个节点的标准化重要性,这意味着在每个视图中所有节点的重要性之和为1。
这段讲自注意力机制比较拗口,建议大家不太明白的话就自己把H和两个权重矩阵取一个很小的维度画出来,跟着公式算一遍就明白了,我图画的比较丑,就不往上贴了,在代码中用两层FC层就实现了自注意力机制,还是比较简单的。
经过上面的流程,我们现在获得了经过两层GCN的特征矩阵 H n × v H^{n×v} Hn×v,自注意力机制评分矩阵 S ∈ R r × n S\in R^{r×n} S∈Rr×n,通过这两个矩阵计算最终的图表示e:
e = S H (7) e=SH\tag7 e=SH(7) 那么e的维度就是 e ∈ R r × v e\in R^{r×v} e∈Rr×v,现在它就跟节点的数量n和节点的顺序都没关系了,我们就实现了尺寸不变性和平移不变性,并且它将通过自注意力机制得到的评分矩阵也编码进了embedding中,就实现了节点重要性。
此外,作者认为SAGE有一个潜在的风险:自注意力机制得到的r个视图有可能是相似的,于是增加了一个惩罚项:
P = ∣ ∣ S S T − I r ∣ ∣ F 2 (8) P=||SS^T-I_r||_F^2\tag8 P=∣∣SST−Ir∣∣F2(8) 其中, ∣ ∣ ⋅ ∣ ∣ F ||\cdot||_F ∣∣⋅∣∣F表示Frobenius范数。最后这个惩罚项没怎么看懂,论文里没说为什么会有这么个风险,也没说这个惩罚项是怎么起作用的,有知道的朋友可以在评论区交流一下。
到这里我们的IC分类器就结束了,论文里说的IC实际上就是这个SAGE,然后加了一个图级(图实例)分类的输出,HC里面就是两层GCN做了一个节点级分类(这里的节点是层次图的节点,也就是IC里的图实例,IC和HC进行分类的是一个东西,这样我们的损失函数里才算散度,时刻记住我们的任务是做层次图中每个节点的图实例的分类)。现在我们就可以训练我们的模型了。
算法描述与解释
文章提出了两种层次图半监督分类的框架:SEAL-CI和SEAL-AI。SEAL-CI就是无人参与的,每一轮把unlabel的样本中挑出n个置信度最高的样本(如何判断置信度?算两个分类器IC和HC的散度,这两个分类器的预测结果越相近,我们就认为置信度越高)加入到label的样本集里面,这样进行很多轮,直到所有unlabel的样本都被打上标签。SEAL-AI则是有人工参与的,它跟SEAL-CI的区别在于,每一轮选出n个置信度最低的样本,由人打上标签,再加入到label的样本集合里,我们主要关注SEAL-CI方法。


实验
本文实验用了两个数据集,第一种是用七种图生成算法生成的图实例,插入到基准数据集Cora的拓扑结构中,即数据集Cora提供合成层次图的骨架(即边),不同图生成算法生成的图作为节点的图实例。图6是这些生成的图实例的一些性质(平均值)。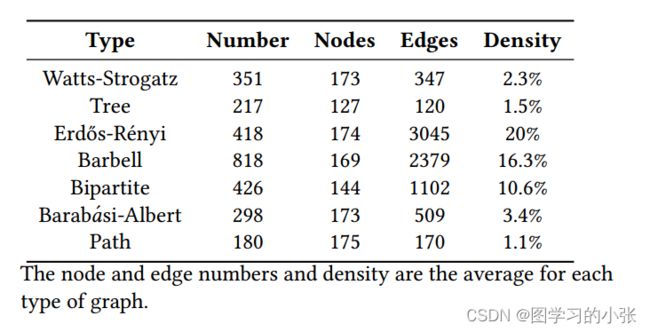


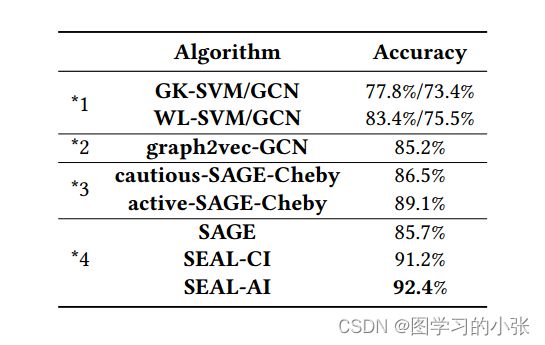
对比实验的结果:


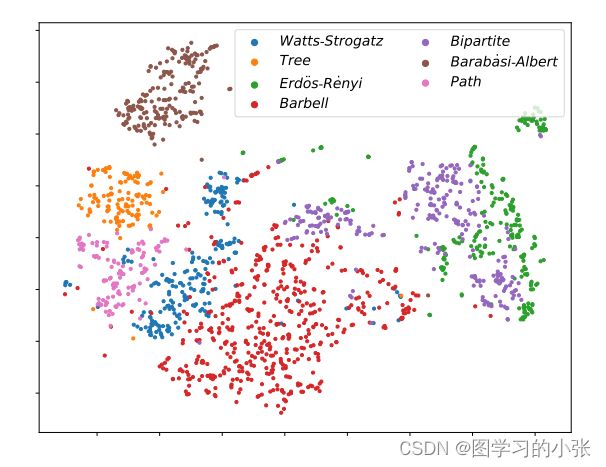
论文对模型的结果做了一个可视化:
参考文献
[1]. Li J , Rong Y , Cheng H ,et al.Semi-Supervised Graph Classification: A Hierarchical Graph Perspective[J]. 2019.DOI:10.1145/3308558.3313461.
[2].Jia Li, Yongfeng Huang, Heng Chang and Yu Rong. Semi-Supervised Hierarchical Graph Classification. arXiv:2206.05416v2 , 2022.
这篇文章的作者在2021又发了一篇跟这个很像的文章,就是参考论文2,做的改进是加了一个互信息,没太看懂,又往前面看互信息那篇文章去了,有时间会更出来。
对图的嵌入表示不太明白的朋友可以去读一下我的另一篇笔记:论文笔记:DeepWalk与Node2vec
欢迎点赞 关注 留言交流 如有错误敬请指正!