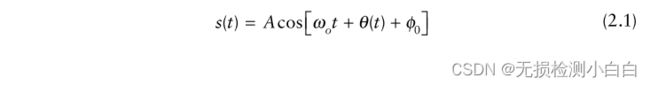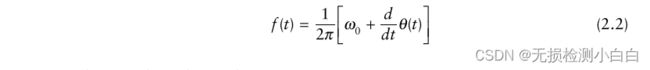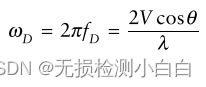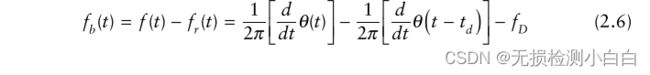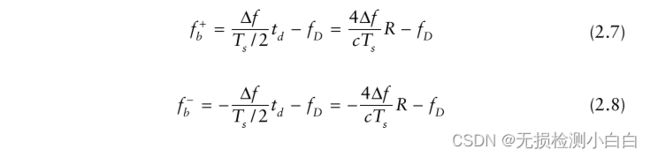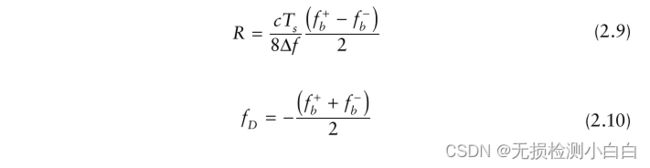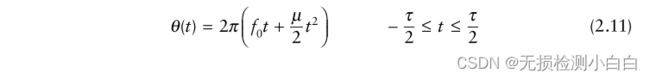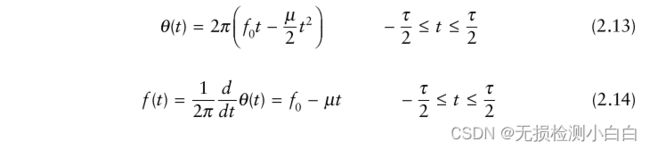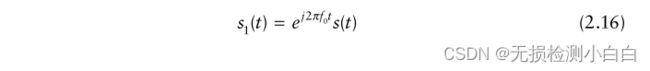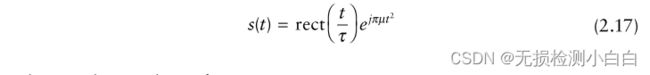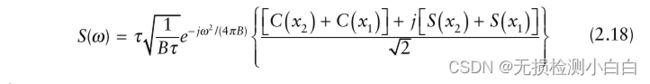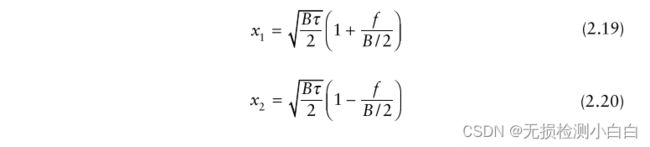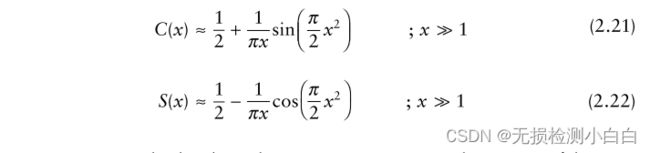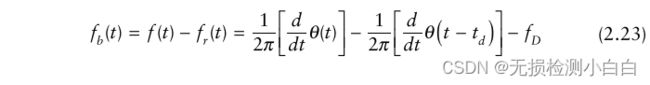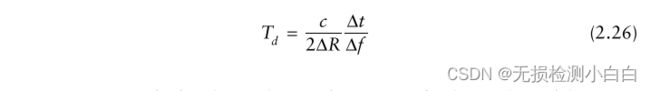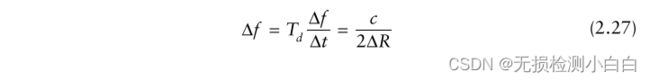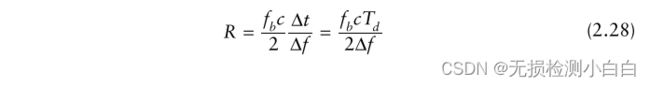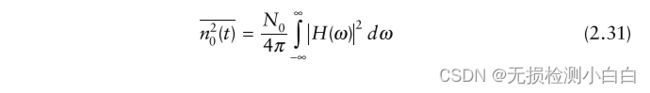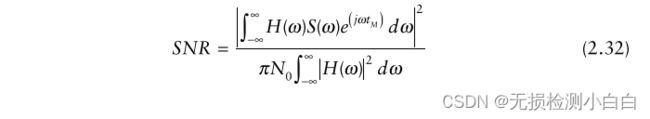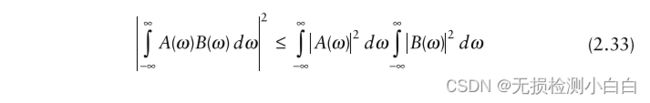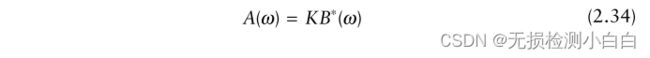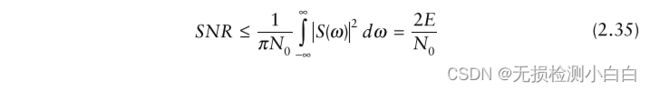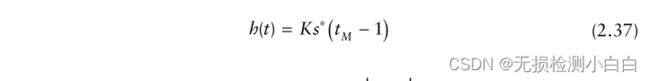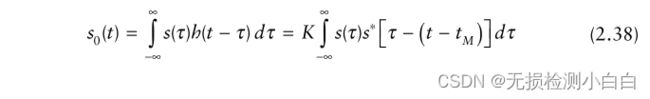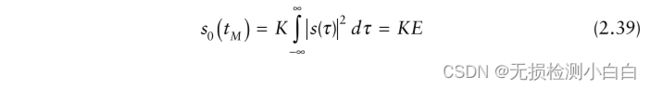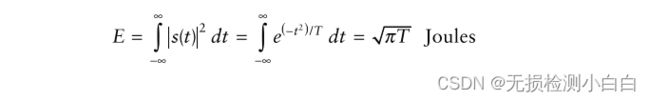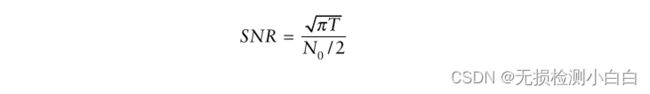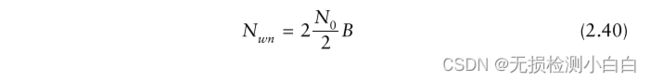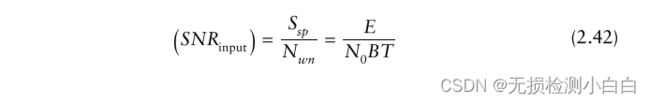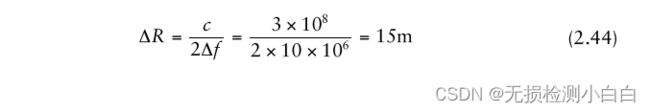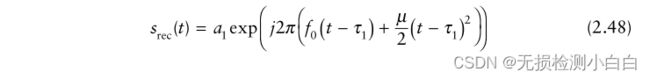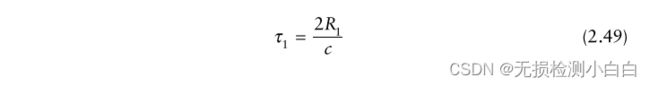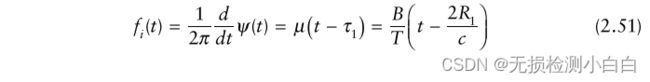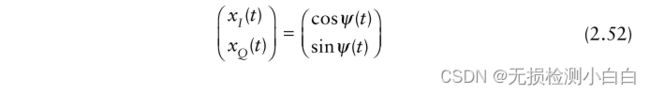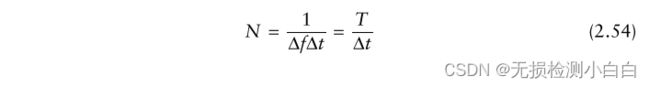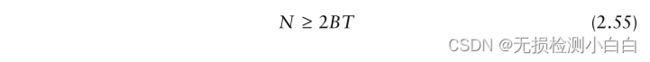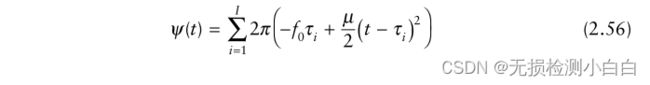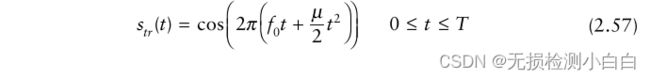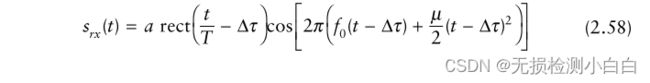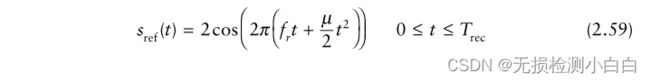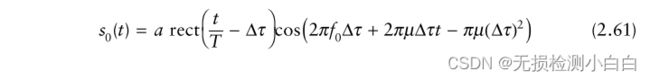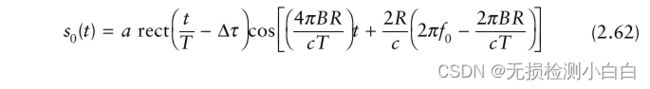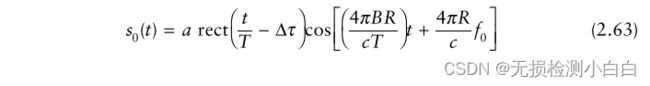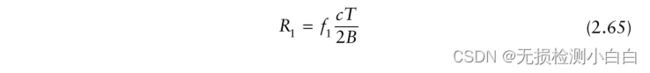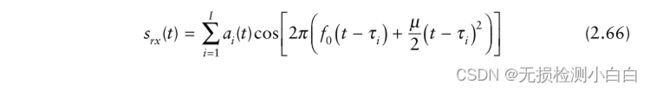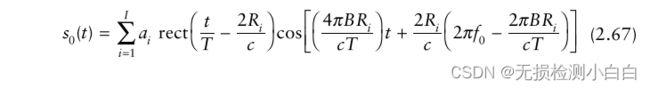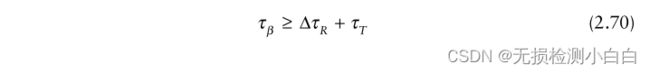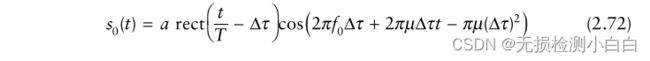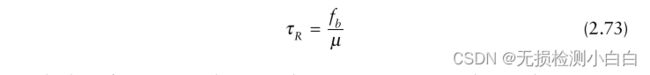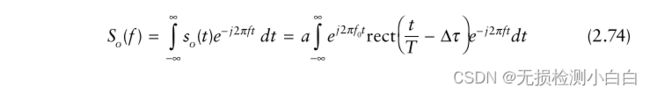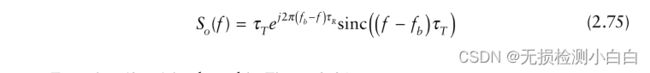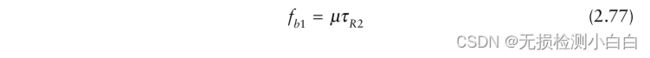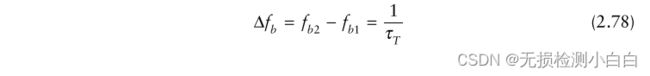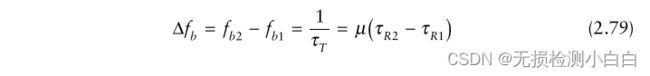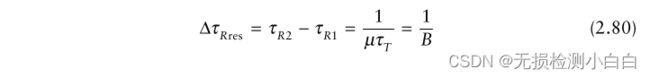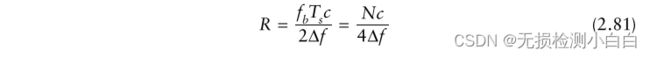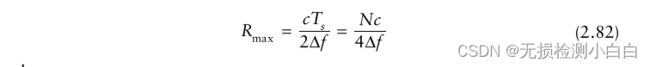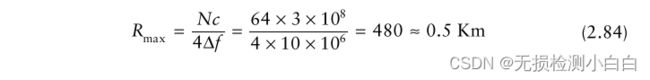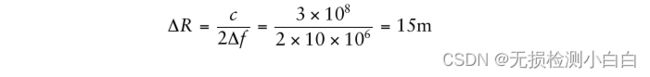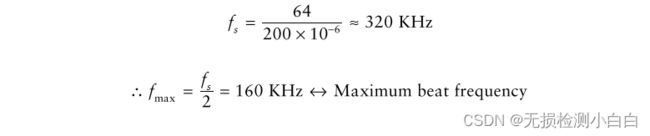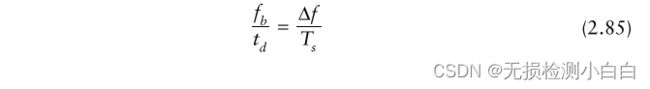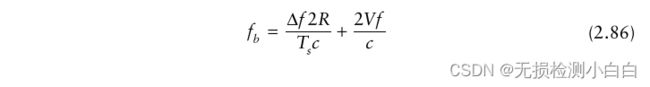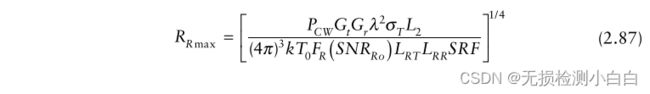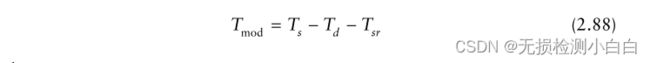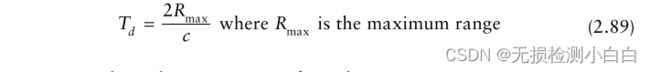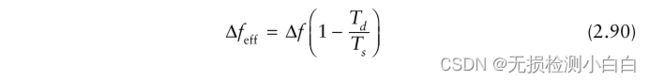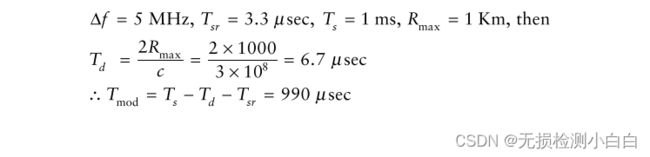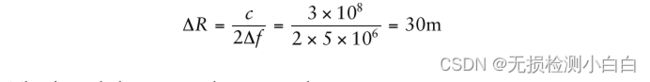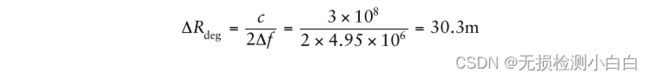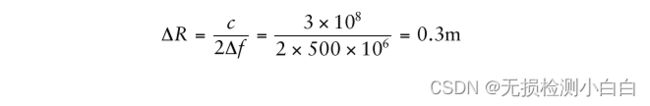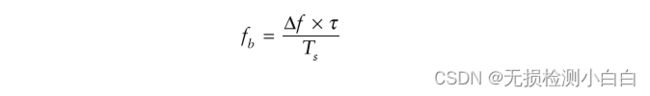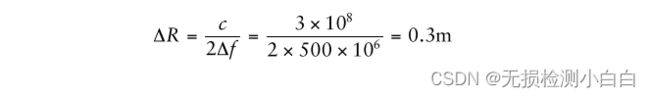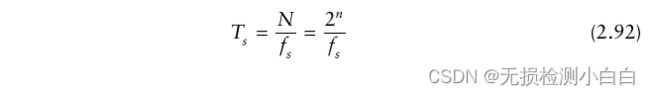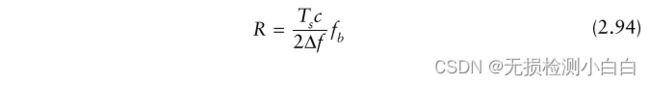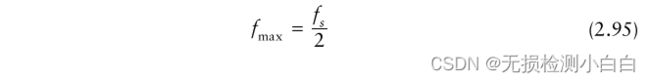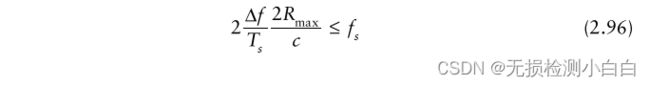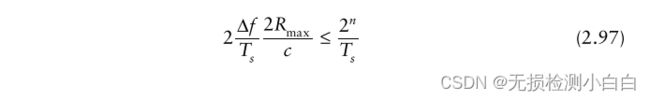【FMCW毫米波雷达设计 】 — FMCW波形

原书：FMCW Radar Design

1  引言

        本章研究驱动FMCW雷达的主要波形:线性调频(LFM)波形。我们研究信号的行为及其性质。随后，本章讨论了匹配滤波理论，并研究了压缩这种波形的技术，特别是所谓的拉伸处理，它赋予FMCW雷达极高的压缩比。最后，本章详细介绍了FMCW技术背后的数学原理，包括距离分辨率问题、带宽问题和整体性能问题，包括LFM波形的非线性及其影响。

2  FMCW 调频连续波

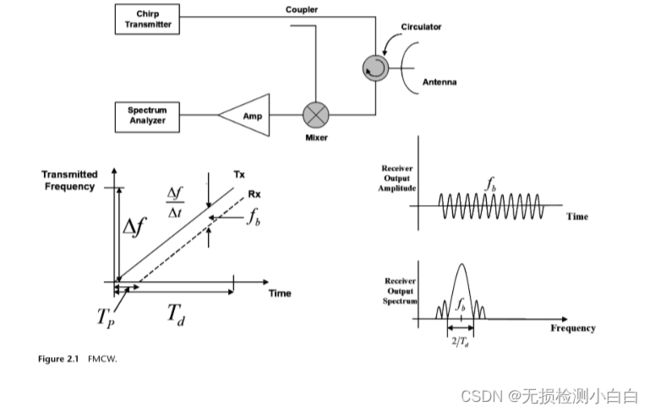
       FMCW雷达与脉冲雷达的区别在于电磁信号是连续传输的[1,2]。这个信号的频率随着时间的变化而变化，通常是扫过一个设定的带宽。发射和接收(反射)信号之间的频率差是通过混合这两个信号来确定的，从而产生一个新的信号，可以通过测量来确定距离或速度。锯齿函数是最简单的，也是最常用的，用来改变发射信号的频率模式。FMCW雷达与传统脉冲雷达系统的不同之处在于射频信号是连续输出的。因此，不能直接测量到反射物体的飞行时间。相反，FMCW雷达发出的射频信号通常是线性扫频的。然后接收到的信号与发射的信号混合，由于反射信号的飞行时间造成的延迟，会有一个频率差，可以作为低频范围的信号检测到。图2.1是一种基于循环器的通用天线系统的示意图。然而，通常有两个完全独立的天线，一个用于传输，一个用于接收。在这种情况下，问题是要确保天线之间足够的隔离。问题是:为什么我们需要锯齿函数，或者任何频率调制?没有调频的简单连续波雷达设备的缺点是，它们无法确定目标距离，因为它们缺乏必要的计时标记，使系统能够精确计时，测量发射和接收周期，并将其转换为距离。可以产生这样一个时间基准来测量静止物体的距离使用频率调制的发射信号。在这种方法中，一个信号在频率上周期性地增加或减少。当接收到回波信号时，频率的改变会得到延迟Δt就像脉冲雷达一样。然而，在脉冲雷达中，运行时必须直接测量。在FMCW雷达中，测量实际发射信号和接收信号之间的相位或频率差异。

        FMCW雷达的特点如下:

        距离测量是通过将接收到的信号的频率与参考信号(通常直接是发射信号)进行比较来完成的。

        发射信号的持续时间大大大于所安装的距离测量范围所需的接收时间。

        FMCW雷达的基本特点如下:

        能够测量非常小的范围到目标;

        能够同时测量目标距离及其相对速度;

        量程测量精度极高;

        低频范围混合后的信号处理性能，大大简化了处理电路的实现;

        安全无脉冲辐射，峰值功率高。

        我们现在更详细地研究FMCW波形，作为其他技术的背景。

3  线性调频波形

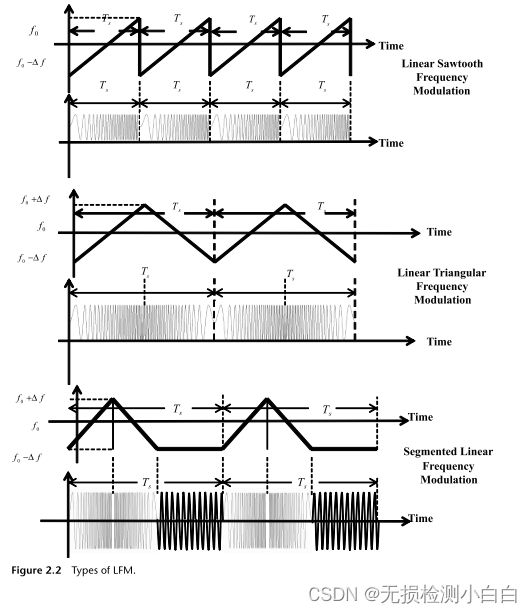
        在我们对高分辨率的追求中，我们被驱使着去追求更高带宽的信号。LFM就是这样一个信号[1−3]。这是非常受欢迎的，而且有充分的理由，我们将会看到。基本上有三种LFM波形，它们在隐形雷达中非常流行:

        1. 线性锯齿波调频;

        2. 线性三角调频;

        3. 分段线性调频。

        这些调制形式如图2.2所示。

4  线性锯齿FMCW

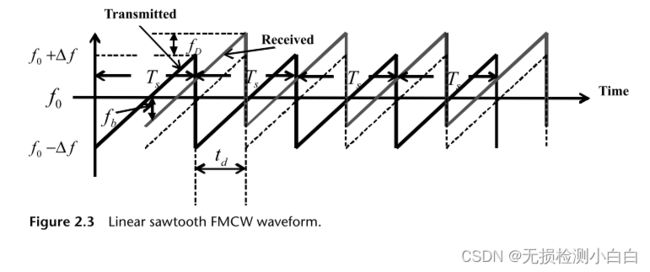
        这类信号的连续波形以锯齿状的方式传输，如图2.2顶部所示。它的方程由，

        ​​​

         这个信号的频率由，

         其中θ(t)斜率为线性。

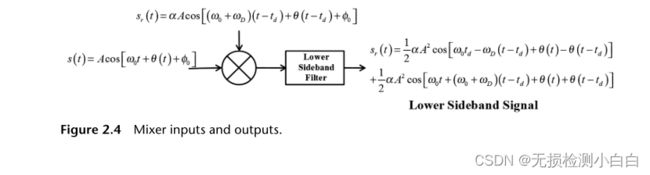
        接收到的信号为:

        其中

                       α是衰减因子

                        td = 2R/c为到目标的双向时延

               是多普勒频移，Vcosθ是径向速度，λ是波长

                接收信号的频率由

        显然，从图2.3中可以明显看出，发射波形和接收波形之间的差值构成了理想的纯正弦波，称为拍信号fb。这个拍频信号正比于发射波形和接收波形之间的延迟，换句话说，就是目标距离。此外，接收的波形相对于发射波形向上移动(对于后退的目标)(见图2.3)。这是由于目标多普勒，其值fD为(2.4)所定义的目标多普勒。锯齿波形的周期称为扫描时间，Ts。注意td是到目标的双向时间延迟，沿x轴测量，而在频率或y轴上的对应信号是fb，拍信号。

        我们现在需要提取拍信号，fb。显然，这可以通过减去发射和接收的波形来实现。这是通过混合(乘)这两个信号和过滤下边带保留频率的差异来实现的。从数学上(见图2.4)，如下所示:拍信号的频率为，

         因此，返回信号的频率与发射信号的频率发生了变化，原因如下:

                 双向时延 td = 2R/ c;

                 多普勒频移 

        

        我们从图2.5中注意到，

         因此，我们有两个方程，两个未知数，R和fD，其解，

 

         通过FFT得到fb +和fb−。利用这些和(2.9)(2.10)计算R和fD。然而，图2.5中有一些有趣的地方。如果目标接近雷达，我们就会遇到向上多普勒情况。相反，如果目标远离雷达，我们就会遇到下多普勒情况。例如，在上多普勒情况下，接收到的波形沿y轴(频率轴)向下移动，如图2.5所示。这是因为基本拍信号增加了目标的多普勒。如图2.5所示，这意味着在没有目标多普勒(静态目标)的情况下，拍频信号相对于标称值的频率会增加。相反，在下降多普勒期间，接收到的波形将沿着频率轴向上传播，降低拍信号的频率。因此，总结起来，上多普勒增加了节拍信号的真实标称值(这取决于目标的距离)，而下多普勒降低了节拍的频率信号不要忘记拍信号的频率是由图2.5中发射和接收波形之间的间隙给出的。读者可以更容易地通过查看图2.5的顶部图来理解这个问题，图中包含了发送和接收波形。然而，我们知道拍信号的频率与目标距离直接相关。(我们稍后将在第2节中讨论这些方程。)但真实目标距离受到目标多普勒的影响，因为由于目标多普勒的作用，拍频信号的频率从其真实值变为目标静态。这种现象称为距离-多普勒耦合，其中由于目标多普勒而产生距离误差。第三章探讨了这些问题。在图2.5中，多普勒滤波器在上多普勒(或拍信号增大)时出现4个峰值，而在下多普勒情况下，滤波器1出现峰值，因为拍信号频率减小。因此，我们可以直接读取fb +和fb−，然后计算距离和多普勒。请注意，在图2.5中，如果没有目标多普勒(即目标是静态的)，那么拍信号波形将是围绕x轴对称的。

4.1  线性调频波形

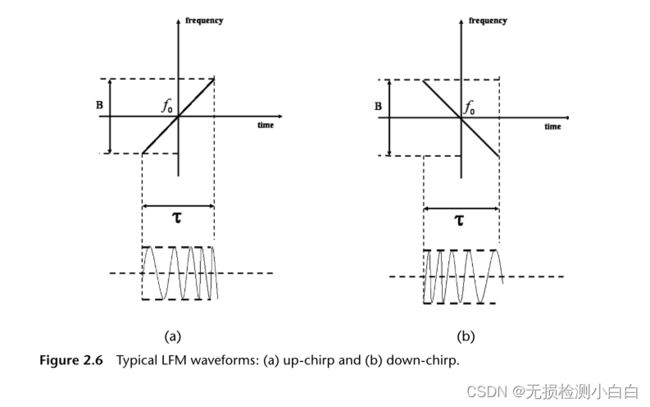
         现在我们考虑锯齿波形本身。我们基本上有两大类线性调频信号定义的线性扫描特性，上行啁啾或下行啁啾。匹配的滤波器带宽与扫描带宽成正比，与脉冲宽度无关。图2.6显示了两种LFM信号。

         线性调频上行啁啾瞬时相位表示为

       图2.5 FFT捕获目标多普勒(下图为下多普勒情况，拍频从静止的目标频率值[雷达回波虚线波形]开始下降)。

        式中，f0为雷达中心频率，μ = (2πB)/τ为LFM系数。因此瞬时频率为

        类似地，对于下啁啾，

        一个典型的LFM波形在时域[1]中有如下表达式:

                其中

                        表示宽度为τ的矩形脉冲。

                        (2.15)可以改写为

                 其中

                是s1(t)的复包络线。

        在频域，(2.17)的FT经过一些操作后得到[1]

      

                其中

              

                菲涅耳积分，用C(x)和S(x)表示，定义为

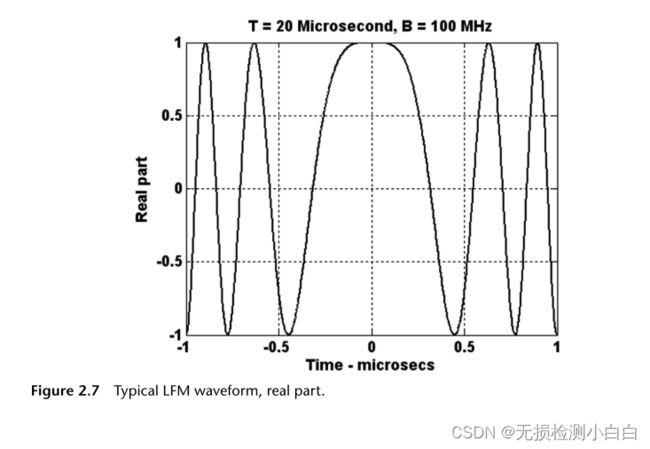
        图2.7 ~ 2.9显示了LFM信号的实部、虚部和频谱。LFM带宽为100 MHz，未压缩脉冲宽度为20 μs。

5  线性三角形FMCW

         信号处理的初始阶段与锯齿波形的初始阶段相同。与锯齿波形(见图2.10)一样，接收到的拍信号由(2.6)给出，重现如下:

        同样，目标的距离和多普勒由(2.9)和(2.10)定义。然而，相似之处就到此为止了。当评估多个目标时，三角波形会产生问题。我们将从一个目标开始，就像处理锯齿波形一样。

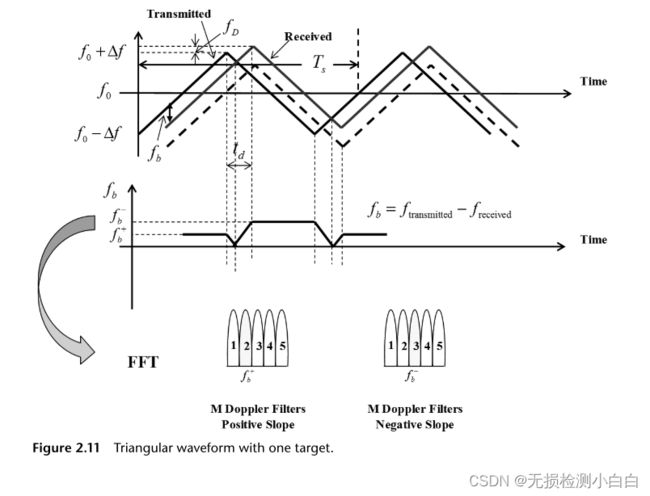
5.1  单个目标

        当我们对正斜率进行FFT时，我们得到，而在负斜率上，我们得到。如图2.11所示。在这种情况下，R和fD由(2.9)和(2.10)定义。然而，如果有两个目标，那就完全是另一回事了。

5.2  两个目标

        在这种情况下，如图2.12所示，当我们对每个正斜率和负斜率进行FFT时，我们在每个多普勒窗口得到两个节拍，我们不能将哪个节拍与哪个目标相关联。我们通过添加一个未调制的线段[1]来解决这个问题。

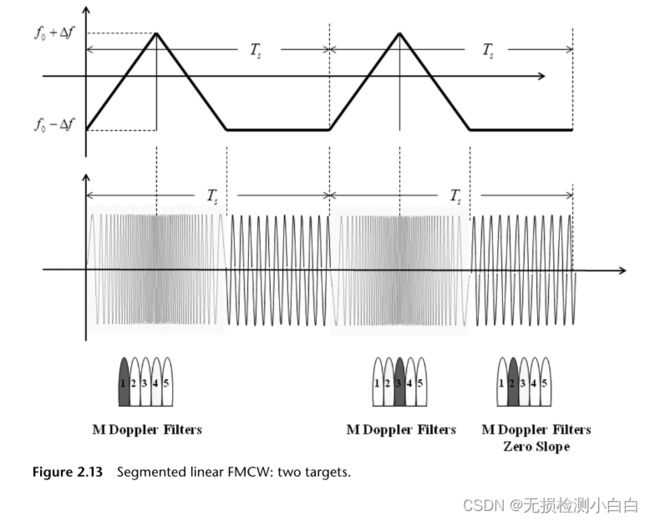
6  分段线性FMCW

        在图2.13中，正斜率产生了两个回波。同样，负斜率也产生了另外两个回声。然而，为了解决歧义，我们使用一个零斜率的未调制截面。这能得到每个目标的准确多普勒信号。知道多普勒值后，我们将和代入(2.10)，直到满足该方程。这意味着这个联想是正确的。现在我们可以使用(2.9)来计算距离。另一种解决距离和多普勒模糊的方法是使用许多调制斜率(Δf 和 )。 

        我们现在计算FMCW雷达的两个主要参数:扫频带宽和到目标的距离。

7  扫描带宽的推导

        载波频率随时间线性增加[1−5]。坡道坡度由Δf/Δt给出。在往返时间Tr = 2R/c后接收到回波，其中R为到目标的距离。

        回波与部分发射信号混合(零拍混合)以产生输出拍频fb。

         从图2.1可以看出，输出将是一个恒定的频率，除了在周转时间的扫描的极端。

         如果所需的距离分辨率为ΔR，则所需的频率分辨率为

 

         对于的光谱分辨率，信号必须观测到Td = 1/的最小驻留时间

    

         在斜坡速度为Δf/Δt时，总扫频 Δf 是扫频和停留时间的乘积:

 

         式(2.27)表示所需距离分辨率越高，所需信号带宽越大。这个推论与脉冲雷达的推论是一样的。

8  计算距离

        一般来说，使用下面的关系从测量到的拍频计算出距离

       

        注意，Td是传播到目标的时间(范围)，也是所需光谱分辨率的最小驻留时间[见(2.26)]。扫描时间Ts是FMCW波形的总扫描时间，比Td大得多。原因将在2.16节稍后讨论。

9  匹配过滤器

        匹配滤波器[1−4]是这样一个滤波器，其脉冲响应由这样一个特殊的信号决定，当信号和白噪声都经过滤波器时，滤波器输出的信噪比可达到最大。这种滤波器广泛应用于雷达。

        考虑一个带有加性高斯白噪声的双侧信号s(t)，其谱密度为N0/2，通过一个频率传递函数H(ω)的线性滤波器。摆在我们面前的问题如下:

        在给定的观测时间tM下，输出的信噪比最高的滤波器响应是什么?

        因此，我们需要寻找这样一个传递函数H(ω)来完成这项工作，并使所给的信噪比最大化

        如果s(t)的傅里叶变换是s(ω)那么 tM 处的输出信号由

        将(2.30)和式(2.31)代入(2.29)得到

        我们现在使用Schwartz不等式，它说对于任意两个复信号A(ω)和B(ω)，下面的不等式是成立的

        这个等式成立

        其中 * 为复共轭，K为任意常数。

        将Schwartz不等式应用于(2.32)，我们得到

        E是信号的能量。此时为相等，即最大信噪比

        由式(2.35)可知，2E/N0是可达到的最高峰值信噪比。H(ω)的傅里叶反变换将产生所需滤波器的脉冲响应

        检查(2.37)可知H(ω) = K⎪S(ω)⎪，这意味着滤波器根据信号的频谱来衡量其频率响应。脉冲响应表明它是信号共轭的延迟镜像。对于因果滤波器，当t < 0时，h(t)必须为零。这只有在tM等于或大于信号的持续时间s(t)时才会发生。

        如果我们将输入信号与与之匹配的滤波器的脉冲响应卷积，我们得到

        如果让 t = tM ，就得到

        即在tM处，输出信号与输入信号的能量成正比。这适用于所有通过其匹配滤波器的信号。

        因此，综上所述[4,5]，在白噪声存在的情况下，匹配滤波器的输出信噪比是可达到的最高的:2E/N0。这个输出信噪比是信号能量E的函数，但不是信号的形式。当噪声是非白噪声时，或者当分辨率、精度和检测等其他因素很重要时，信号的形式就很重要了。

        例子

        当脉冲响应匹配到信号s(t) = exp(−t2/2T)时，线性滤波器输出的最大瞬时信噪比是多少?

        答案

        信号能量为

        因此，最大瞬时信噪比为

         式中，N0/2为输入噪声功率谱密度。

10  存储副本

        匹配滤波器输出可以从雷达接收信号和发射波形的延迟副本之间的互相关计算出来。在数学上和结构上，这与(2.37)中给出的表达式所定义的是一样的。如果输入信号与发射信号相同，则匹配滤波器的输出为接收(或发射)信号的自相关函数。这是一种非常流行的实现这种滤波器的方法，在实践中，传输波形的副本通常被计算并存储在内存中，以供雷达信号处理器在需要时使用。

11  时间-带宽乘积

        我们现在检查一个匹配的滤波雷达接收机。滤波器具有前面讨论过的双侧频谱的白噪声带宽。这个噪声功率由

        其中B是匹配的滤波器带宽，用2的因子来考虑负频段和正频段，如图2.14所示。

        在信号持续时间T内的平均输入信号功率为[2]

         其中E为信号能量。因此，匹配的滤波器输入信噪比为

        输出峰值瞬时信噪比与输入信噪比为

        数量BT被称为给定波形或其相应匹配滤波器的时间-带宽乘积。输出信噪比比输入信噪比增加的因数BT称为匹配滤波器增益，或压缩增益。

        未调制信号的时间带宽乘积接近统一。我们可以通过使用频率或相位调制，使信号的时间和带宽乘积大于一个单位。如果雷达接收匹配滤波器与输入波形完全匹配，压缩增益等于BT，如果匹配滤波器频谱偏离输入信号的频谱，压缩增益成比例下降。

12  波形压缩

        为了在雷达中获得高分辨率，必须增加信号带宽。这在非调制脉冲雷达中是通过发射非常短的脉冲来实现的。然而，如果我们使用短脉冲，我们也降低了平均发射功率，因此，雷达探测距离。因此，我们需要寻找一种方法，使我们能够以较大的平均功率(通过使用长脉冲)发射，同时实现与短脉冲相同的距离分辨率。随着线性调频脉冲的出现，这种异常情况得到了解决。LFM脉冲利用宽带宽和大平均功率发射一个长脉冲，然后使用下面讨论的脉冲压缩技术对接收的脉冲进行压缩，以达到预期的距离分辨率。因此，脉冲压缩可以让我们获得长脉冲的平均发射功率，同时获得短脉冲对应的距离分辨率。在连续波雷达中，我们用波形压缩来代替脉冲压缩。从此以后，我们将在本书中使用这个术语。

        有两种著名的技术来实现波形压缩:

                相关处理;

                拉伸加工。

12.1  线性调频波形压缩

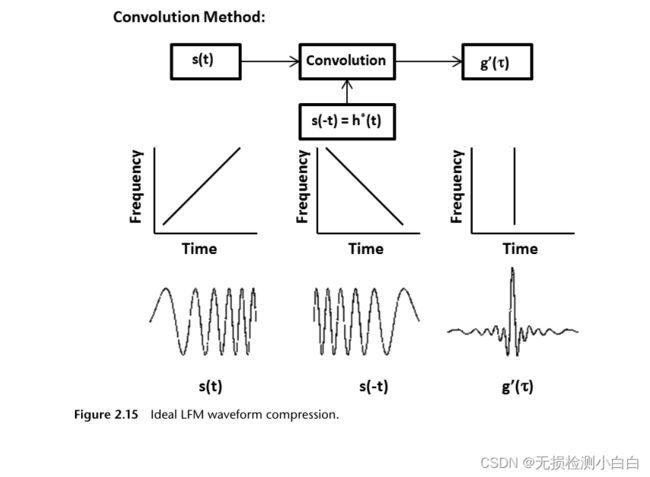
        LFM波形压缩是通过在传输时对长啁啾信号进行调频和使用匹配的滤波器接收机来压缩接收到的信号来实现的。因此，匹配的滤波器输出被一个因子BT压缩，其中T是未压缩的信号宽度，B是LFM信号的带宽。因此，我们可以使用长啁啾信号和LFM调制来实现大的压缩比。图2.15显示了LFM波形压缩过程。

        图2.15显示了与匹配滤波器进行卷积的LFM波形。匹配的滤波器输入/输出波形也显示出来。与频率域的输入波形相比，输出在时域是一个压缩脉冲。请注意，匹配滤波器的波形是输入信号的镜像逆。

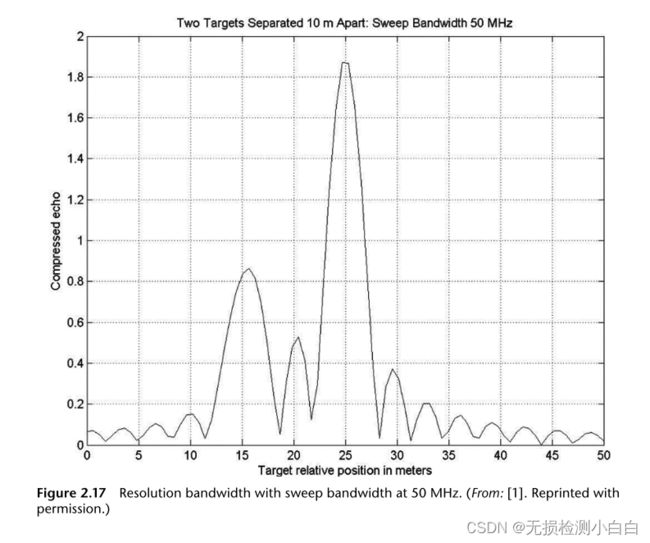
        我们现在检查波形压缩带宽的影响。我们假设在15m和25m处有两个RCS 1 m2和2 m2的目标。在初始情况下，扫描带宽为10 MHz。接收窗口为50m。扫描时间为10 μs。这种情况下的距离分辨率由

        这也被称为瑞利分辨率。由于带宽不足，雷达无法分辨目标。如果我们现在把带宽增加到50兆赫兹，那么

         很明显，雷达现在可以分辨目标。该程序在附带的软件中给出，并命名为“LFM_resolve.m”。结果如图2.16和2.17所示。

        至此，我们已经看到了匹配滤波器是如何进行LFM波形压缩的。但是这种匹配的过滤器是如何实现的呢?

12.2  相关处理器

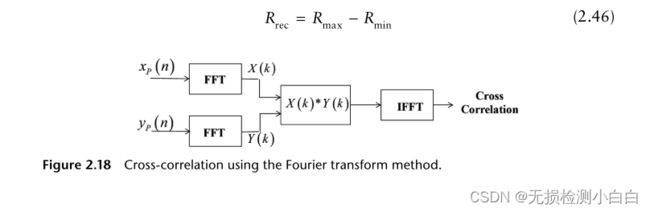
        我们将雷达距离窗口定义为雷达最大和最小距离的差值。这也称为接收窗口。收集接收窗口内的所有目标返回，并通过匹配的过滤器进行波形压缩。这个匹配的过滤器可以通过多种方式实现。一是使用声表面波(SAW)装置[6]。另外，我们可以使用FFT进行数字相关处理。这种方法叫做快速卷积处理(FCP)。如图2.18所示。为了使两个长序列相关联，必须进行傅里叶变换，然后将一个序列与另一个序列的复共轭乘积，最后进行傅里叶反变换完成这一过程。

        将发射序列装入参考寄存器，通过信号移位寄存器对输入序列连续计时。在每个时钟周期上，比较计数器形成匹配的总和，并减去移位寄存器的相应级之间的不匹配，以产生相关函数。这种方法也称为FCP。        

        现在，我们参考FCP来研究这个过程背后的数学原理，如图2.18所示。

        定义的接收窗口

         其中Rmax和Rmin分别定义雷达探测距离的最大值和最小值。归一化复发射信号的形式为[1]

         其中 T 为信号宽度，μ = B/T, B为带宽。

        雷达回波与发射信号相同，但有一个与目标RCS相对应的时间延迟和振幅变化。我们假设目标位于距离R1的位置。这时雷达接收到的回波

         其中a1与目标RCS、天线增益和距离衰减成正比。时间延迟 τ1 由

         最初，我们去除频率fo。这是通过将接收信号srec(t)与相位为2πfot的参考信号混合来实现的。合成信号经过低通滤波后的相位由

         瞬时频率为

         正交分量是

         接下来，我们通过选择采样频率 fs >2b 对正交分量进行采样(以满足Nyquist准则，从而避免频谱中的模糊性)。则采样间隔为 Δt≤1/2B。由式(2.51)可知，FFT的频率分辨率为

        最低要求的采样数量是

        利用 Δt≤1/2B 代入(2.54)得到

        因此，我们需要总共 2BT 的实采样或BT的复采样来完整描述一个持续时间T和带宽B的LFM波形。例如，一个持续时间T = 10 μsec，带宽B = 4 MHz的LFM信号需要80个实采样来确定输入信号 (  i  通道40个采样，q  通道40个采样)。

        假设接收窗口内有I个目标，范围为R1、R2等，那么根据叠加定理，下转换信号的相位为[7-9]

        时间 {τi = (2Ri / c); i = 1,2，…，i} 为双向时延，其中 τi 与接收窗口开始时间重合。该方法已在Simulink®中实现。它在随附的程序中给出(参见FCP.mdl)。

12.3拉伸处理器

        伸缩处理，也称为主动相关，是为了处理极宽带宽的LFM波形。我们现在更详细地研究这一重要技术，因为它在FMCW雷达中非常流行[1,5]。

        我们现在用数学方法证明拉伸信号处理。这是基于[5,6]的推导。归一化后的传输信号可以表示为

        其中，μ = B/T为线性调频系数，f0为调频启动频率。假设距离R处有一个点散射体，雷达接收到的信号为

        其中a与目标RCS、天线增益和距离衰减成正比。延迟时间为Δτ = 2R/c。参考信号为

        接收窗口为

         如果没有传播延迟(即Δt = 0)，则fr = f0，换句话说，fr和f0是相同的频率，唯一的区别是前者属于发射信号，后者属于接收信号。因此，为了这个推导，我们可以声明fr = f0。混频器的输出是接收到的信号和参考信号的乘积。经过低通滤波，

        利用Δτ = 2R/c，代入(2.61)，得到

        由于，T >> 2R/c，我们可以将(2.62)近似为

        瞬时频率为

        这清楚地表明了目标范围与瞬时频率成正比。因此，对LPF输出进行采样并进行FFT后，我们得到

        频率为f1的R1的目标。

        如果有 I 个距离为R1、R2等的近距离目标(R1 < R2 <…RI)，通过叠加得到，总信号为

         其中 {ai(t);i = 1,2，…，i} 与目标的横截面、天线增益、距离成正比。时间 {τi = (2Ri/c); i = 1,2，…，i} 为双向时延，其中τi与接收窗口开始时间重合。使用(2.62)LPF输出的整体信号可以描述为        

         因此，目标返回显示为可以使用FFT分解的恒定频率的音调。因此，确定适当的采样率和FFT大小是关键。在[9]中证明了样本个数N由

         如果我们用匹配滤波器来处理LFM脉冲，匹配滤波器的脉冲响应是，

         我们把rect(x)看成一个偶函数。

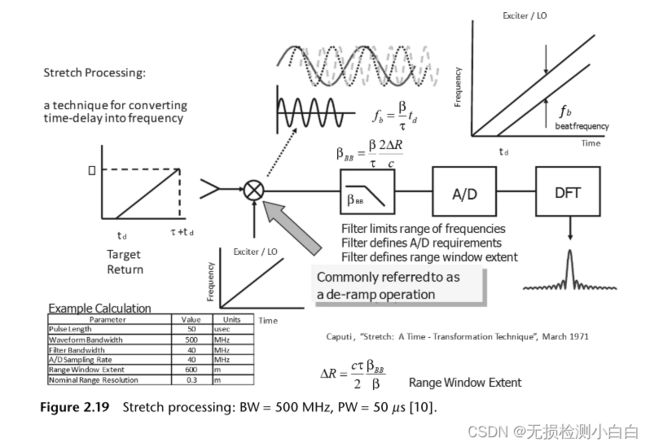
         由式(2.69)可知，匹配滤波器的带宽要求为   。这种宽带信号处理器的成本很高。线性调频匹配滤波器的常用方法是声表面波压缩器和数字信号处理器。声表面波传感器的有效频率可达3ghz左右。如果我们使用数字信号处理器，我们会受到adc采样速度的限制。这通常在3ghz左右。拉伸处理通过放弃整个雷达范围的处理，而支持窄带处理来解决这个难题。在匹配滤波器中，我们将在整个波形脉冲重复间隔(PRI)中寻找目标。另一方面，在拉伸处理中，我们被限制在一个通常小于未压缩脉冲宽度的范围内。因此，拉伸加工在求解距离较近的目标时得到了广泛的应用。然而，必须记住，拉伸处理只能缓解匹配滤波器的带宽要求，而不是整个雷达。例如，天线、发射机和接收机必须有较宽的带宽来处理信号。图2.19总结了拉伸处理中的问题[10,11]

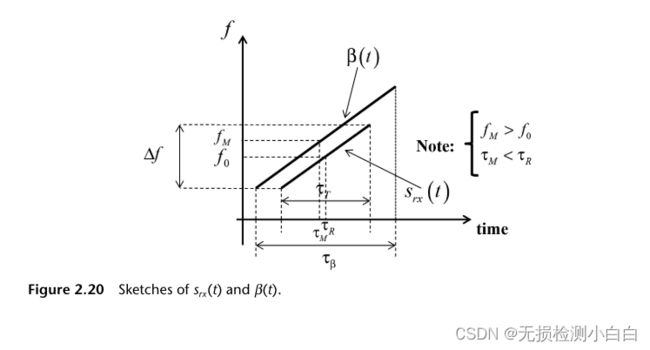
        图2.20给出了srx(t)和β(t)的概念草图。两者都是线性调频信号。它们的频率随时间线性增加。然而，它们的持续时间是不同的。在信号持续时间方面，β(t)总是远远大于srx(t)。两个信号的斜率都是µ。

        图2.20还告诉我们所需的 值，即外差信号的持续时间。对于所有τR的期望值，都需要保证srx(t)完全包含在β(t)内。这意味着，

        其中

        是我们想要执行拉伸处理的范围延迟范围。如果τβ满足上述约束，则β(t)将完全重叠srx(t)，拉伸处理器将提供与匹配滤波器[5]几乎相同的信噪比性能。否则，会有一定比例的信噪比损失。

         Budge[5]和许多作者已经将这种推理提高到一个更详细的水平。如果参考信号β(t)在传递到拉伸处理器的过程中延迟 ，则有两种情况，描述如下。

        1.  > :在这种情况下，参考信号的频率比目标回波的频率低。这意味着拍信号的频率将低于其实际值，而= 。

        2. < :在这种情况下，参考信号的频率高于目标回波的频率。这就意味着当= 时，拍信号的频率将高于其实际值。这就是图2.19所示的案例。

        理想情况下，τM = τR，但这是不现实的。目标延迟和参考延迟将是接近的，大多数分析忽略了这是一个近似值。通常，使用延迟线[1]将参考延迟τM与雷达最近的距离相匹配，因此，几乎总是τM < τR，且在该特定的距离拍信号会有一个高于正常值的值。然而，这种误差是可以忽略的。

12.3.1拉伸处理器操作

        (2.61)是经过低通滤波后的信号，再对其进行复现，

        我们注意到(2.72)的第一项告诉我们混频器的输出是一个与目标范围成比例的恒频信号。因此，如果我们确定出混频器的信号的频率，我们就可以确定目标范围。因为，fb = μτR，其中fb是拍频，我们得到

        拍频是用频谱分析仪确定的。频谱分析仪计算so(t)的傅里叶变换。

        或者

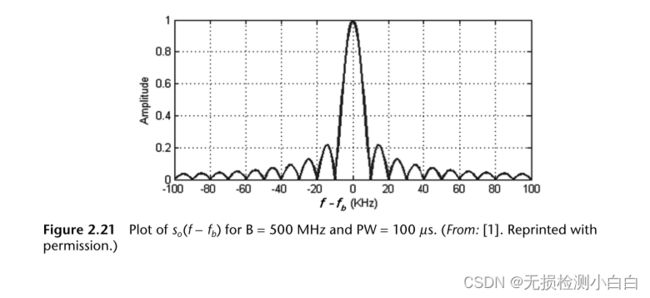
        式(2.75)绘制在图2.21中。

        拉伸处理的距离分辨率是多少? 在图2.21中，我们注意到脉冲宽度是100µs或10 KHz的倒数。这是sinc函数的标称宽度。这也是频谱分析仪的频率分辨率。假定有一个 τR1 范围内的靶，另一个τR2 > τR1范围内的靶。与两个目标相关联的混频器输出频率将为

进一步假设 τR1 和 τR2 是这样的

        拍频由拉伸处理器的分辨率单元分隔。然后我们可以写

         或者

         这意味着拉伸处理器具有与匹配的过滤器[6]相同的分辨率。我们通常可以对输出应用一个加权来减少距离旁瓣。在这种情况下，输出脉冲宽度的宽度取决于所使用的加权类型。下面将对此进行讨论。

        可证明匹配滤波器的输出信噪比与雷达距离方程中使用的信噪比相匹配，拉伸处理器的信噪比与匹配滤波器的 τβ/τT 成正比。有兴趣的读者可以向[5]寻求证据。

        最后，请注意到这一点，我们假设目标是静态的(即，不移动)。如果目标在移动，它就会产生多普勒频移在雷达反射频率中。这一偏移与它的径向速度成正比，拍频必须根据这一多普勒偏移进行相应的修正，如本章前面所讨论的那样。

        关于拉伸加工的更多信息，读者可以参考[1,2,5,7]。

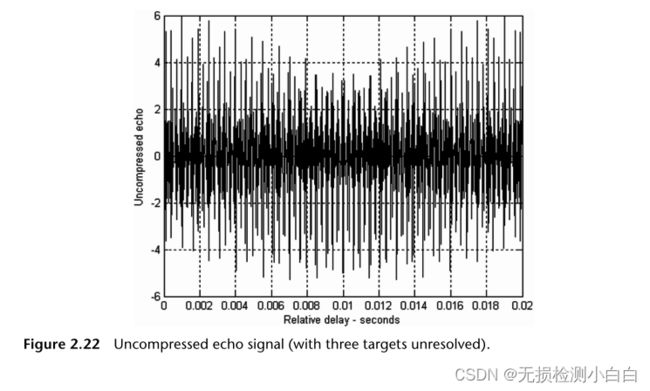
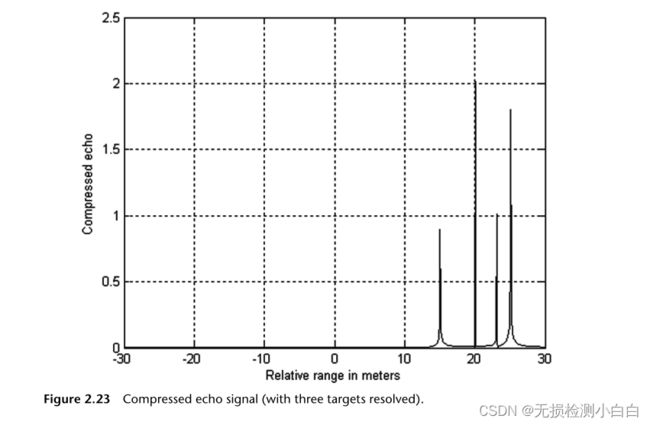
        现在我们检查拉伸处理器的目标解析能力。有一个程序“stretch_processing.M”。我们有四个目标，RCS分别为1、2、1和2，分别位于15、20、23和25米的范围内。假设有一个汉明窗口。假设发射脉冲宽度T为20ms，带宽B为1ghz。图2.22和2.23展示了这种效果。初始频率为5.6 GHz，接收窗口为60m。

        1 GHz带宽的瑞利分辨率是15厘米。作为一个探索性的练习，读者应该试着将目标的距离控制在15厘米以内。雷达将无法分辨目标，除非扫描带宽适当地增加。

        最后，请注意，像声表面波滤波器这样的技术通常会产生大约1000的处理增益，而拉伸处理通常会产生50000的增益。这种类型的处理特别适用于高带宽信号，并利用高达100m的接收窗口。

        必须记住，这种信号处理——尽管它产生了非常高的脉冲压缩度(在啁啾脉冲系统中高达50000对1000)——要求接收信号的开始时间是已知的。在啁啾脉冲雷达中，雷达返回的开始时间是未知的，因为它取决于目标位置。来自不同范围目标的回波具有不同的起始时间，且脉冲持续时间恒定。这使得信号处理变得困难。因此，使用FFT将目标返回值和参考值转换为频域是唯一的选择(相关处理)。然而，在FMCW雷达中，信号是连续的，因此可以方便地应用拉伸处理(在时域工作)。这就是为什么FMCW雷达具有如此高的分辨率(远高于啁啾脉冲雷达)，也解释了FMCW雷达的普及。

        来自同一距离单元的所有返回值产生相同的恒定频率。这种FFT有时也被称为“距离FFT”，因为它处理的是目标距离。在前面的讨论中，我们假设发射的啁啾和接收的啁啾具有相同的斜率。这只在目标是静态的情况下才成立。如果它有多普勒值，那么接收到的回波将有一个递增的频率，这将给拍频一个稳定的附加频率差，与目标多普勒成正比。这将导致范围错误。这种现象称为距离-多普勒耦合，在线性调频波形中表现突出。第3.3节更详细地研究了距离-多普勒耦合。另一个原因是，由于目标径向速度，接收到的脉冲宽度被时间膨胀因子扩大(或压缩)。这种现象可以通过两种流行的方式来纠正:

        1. 我们可以对目标回波进行重复测量，然后确定多普勒值。然后我们调整下一个发射脉冲的啁啾斜率和脉冲宽度，以考虑估计的多普勒频率和时间膨胀。

        2. 我们选择距离单元的宽度，这样信号不会因为目标多普勒而改变距离单元。雷达设计者总是知道最大预期目标多普勒。通常，我们对测量目标多普勒不感兴趣，而只对其距离感兴趣。

      如果要直接测量目标的多普勒，则需要MTD雷达。假设我们有来自同一个目标(在同一个距离bin中)的8个返回值，然后我们将这些返回值路由到一个称为多普勒FFT的8点FFT。这个FFT的输出将是目标多普勒，这将在第三部分进行检查。我们还可以看看图2.23压缩后的回波信号(分解了三个目标)。存储从单一信道返回的8个目标信号，然后将这些信号路由到一个8点多普勒FFT来提取多普勒值。

13  线性调频系统的旁瓣和加权

        由FMCW雷达输出的单目标截断正弦波频谱具有傅里叶理论预测的⎪sin(x)/x⎪特征。

        这种情况下，距离旁瓣仅比主瓣低13.2 dB，这并不令人满意，因为它会导致附近小目标的遮挡，并将杂波从邻近的旁瓣引入到主瓣。为了克服匹配滤波器的这种不可接受的特性，时域信号被故意不匹配。这种失配通常以接收信号幅度加权的形式出现。更多信息请参见[1]。

14  FMCW雷达基本方程

         FMCW雷达的距离由以下关系[1]计算:        

                 R为目标距离;

                Fb是拍频;

                t为扫描时间;

                Δf是扫频带宽或频率偏移;

                C是光速;

                N为所需的FFT大小(点数)。

        我们引入了一个新的变量fmax，它是与最大距离对应的最大拍频。令t = ΔT扫描时间。然后编写FMCW雷达的最大探测距离为

                N为一次扫描时间内的样本个数;

                fmax = fs / 2，其中fs为满足奈奎斯特采样准则的采样频率。

        从前面的章节中我们也知道

        如果我们现在使用64点FFT和扫描时间Ts = 200 μs和Δf = 10 MHz，我们得到

        在这个最大距离下的距离分辨率由

        在扫频时间为200 μs，扫频带宽为10 MHz的情况下，在0.5 km范围内实现了15m的距离分辨率。与此相比，使用LFM脉冲的普通脉冲雷达需要压缩脉冲宽度为100 ns才能实现相同的分辨率。这意味着我们的压缩比是2000，这是非常高的。这是因为FMCW雷达常见的拉伸处理。读者还应该注意，在(2.26)中，扫描带宽在分母中。这意味着整个雷达接收窗口的距离分辨率是恒定的，因为接收窗口中的所有目标都将经历相同的扫描带宽。因此，我们可以预期，与脉冲雷达一样，距离分辨率应该始终是一个常数，而与目标距离无关。然而，在现实中并非如此，因为在FMCW雷达中，距离分辨率是以下函数的函数:

               扫描时间;

                非线性

        为了在一次扫描中产生64个样本(即进行64点FFT)，采样频率

        因为我们有64个采样/扫描，所以我们使用64点FFT来确定距离。然而，实采样的光谱是对称的。因此，我们只需要使用光谱的一半(即在我们的示例中为32)。因此，距离单元格的数量是32。然而，我们需要处理两个频谱的一半，否则我们将失去一半的功率(即，我们进行复杂的处理)[1]。

14.1 FMCW方程

        频率偏差、调制周期、拍频和 转换时间之间有直接关系。这种关系称为FMCW方程[1]。

                Fb是拍频

                td是往返传播时间延迟= 2R/c，其中R是到目标的距离

                Δf是扫描带宽或频率偏差

                 Ts为调制周期(扫描时间)

        鉴于距离-多普勒耦合固有的线性调频波形态如前所述，上扫的拍频取决于距离和速度。

                V 为目标相对于雷达的速度(即径向速度)

                f 为标称雷达频率

        (2.86)中的第二个表达式构成了目标的多普勒频移。为了解决这种耦合，我们需要有两个频率转换速率或斜率。或者，将距离-多普勒耦合控制在一个距离单元内。

15  FMCW雷达距离方程重估

        雷达的距离是由

        我们用输出信噪比和扫描重复频率来表示雷达距离方程。式(2.87)和(1.15)是该方程最常用的形式。就像在低噪声放大器(LNA)的输入端测量输入信噪比一样，输出信噪比在最终中频滤波器(标记RF级的末端)的输出端或范围FFT的输出端测量。(这意味着距离FFT的处理增益也被考虑在内。)

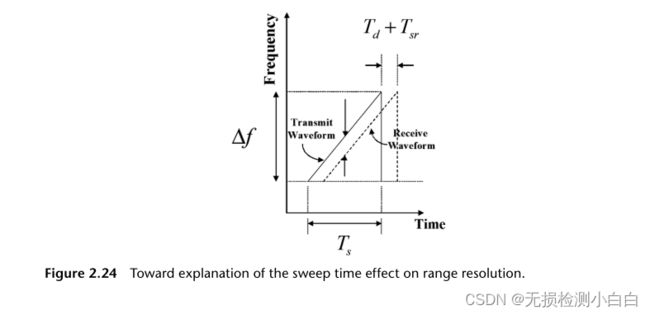
16  扫描时间对距离分辨率的影响

        到达目标和返回的总时间延迟由两个因素[1−3]造成，如下所示(见图2.24):

                1. 往返传播延迟到最大距离;

                2. 扫描恢复时间Tsr。这是在一次扫描结束和下一次扫描开始时所经过的时间。因此，如果Ts是扫描周期:

        因此，在我们获得最大范围的返回值之前，我们无法处理范围fft。这将导致Δfeff给出的有效处理带宽减少

        因此，降级的距离分辨率ΔRdeg由

        例1

        现在我们使用一个示例来更好地解释流程[1]。假设我们有以下参数:

        6.7 μs的切换时间加上3.3 μs的扫描恢复时间使扫描带宽减少了0.05 MHz。这使得有效传输带宽为4.95 MHz。

        理想的距离分辨率是

        降级的距离分辨率现在变成

        这是最坏的情况(即，在最大距离下，距离分辨率是最小的)。它在近距离变得越来越好，因为Td值随着我们靠近雷达而减小。因此，通常情况下，调制周期Ts至少保持在最大范围内传输时间的5倍，因此有效处理带宽至少是总带宽的80%[2,3]。

17  仪器量程的概念

        通常，雷达距离方程(2.87)和(1.22)给出的是雷达的能量范围。在给定发射机功率水平和其他雷达参数，以及目标类型和传播条件的情况下，这是一个人可以达到的距离。然而，我们通常允许显示上的雷达距离刻度稍微超出这个能量范围，通常多出30%。这个距离称为雷达仪表距离。这是雷达设计的覆盖范围(也就是说，它是仪器化的)。例如，一种雷达的能量范围可能是2公里，但仪器的距离可能是3公里。理想情况下，设计师应该努力使仪器测量范围尽可能接近能量范围，否则这是毫无意义的，因为雷达不会探测到超过能量范围的东西。换句话说，雷达接收窗口变得过多。这将导致提供更高的拍频，从而更高的中频滤波器带宽，比通常可以预期的基于雷达规格。这反过来又需要更高的采样频率。因此，应尽量避免过大的仪器测量范围。

18  非线性调频波形

        为了说明这个问题，我们利用(2.87)根据以下参数确定最大距离(也称为能量距离):

        所需距离分辨率:

        雷达参数为

        使用(2.91)，我们实现了一个2平方米目标的能量距离Rmax为993米。

        该雷达的拍频由

        此Rmax的往返传播时间为6.62 μs。

        因此，

        这产生3.3 mhz /993m或3323.3 hz /m拍频率范围比(比例因子，SF)。

        这种雷达的理想距离分辨率是

        因此0.3 m距离分辨率需要996.98-Hz的接收频率分辨率，因此频率扫描线性为500-MHz频率偏差的0.0002%。因此，这是需要的线性，以达到我们期望的0.3m的距离分辨率。读者可以验证较高的非线性，例如0.04%不满足我们的要求。

        这使得我们可以使用数字FMCW发生器，比如DDS[1]。这种发生器在扫描的末端不会有不连续，因为扫描的末端是门控的。这种方法叫做消隐。

19  相干处理间隔

        我们需要确定距离FFT的大小。我们将经过处理的采样与调制周期进行匹配，条件是采样的个数为2的幂。这就产生了

 

        其中是采样，所以

        利用FMCW方程(2.85)，我们可以通过重新排列这些项，用拍频来表示距离。

        我们知道最大拍频

        将(2.95)代入fmax，得到

        利用第18节的例子结果，我们得到fmax = 3.3 MHz。因此，fs必须至少是6.7 MHz。

        现在将(2.93)代入(2.96)得到

        所以

        再一次，使用2.18节中的例子，(2.98)的左边是6,620，所以右边必须是8,192或; 8192个采样在1毫秒内对应8.192兆赫兹采样频率。8192点FFT将覆盖高达4.096 MHz的拍频，对应距离高达1232米。拍频采样间隔为1khz，对应的距离间距为0.3m。汉明窗的频率分辨率等于6 db带宽1.81乘以1 KHz频率采样间隔或1.81 KHz，在距离内对应0.545m。

20  小结

        本章研究了FMCW雷达的基本设计理论，检验了FMCW雷达的方程。研究了目标多普勒对雷达性能的影响及其测量方法。接下来，本章研究了FMCW雷达距离方程，并从输出信噪比和扫频重复频率(而不是扫频带宽)的角度推导出了它的新形式。这种形式在FMCW雷达设计中得到了广泛的应用。随后，我们研究了影响距离分辨率的因素(例如，扫描次数和拍频分辨率)，特别是像目标返回光谱宽度和接收机频率分辨率这样的问题，它们在决定拍频分辨率方面起着关键作用，从而导致最终的接收机距离分辨率。最后，通过实例，本章讨论了FMCW波形的非线性问题及其控制。这需要在雷达没有过度仪表化的距离的情况下完成。