【贪心】经典贪心算法问题——活动安排问题、最优装载问题、单源最短路问题实验报告(C++代码实现)

---

问题来源

《算法设计与分析》教材实验作业——贪心算法

---

一、会场安排问题

1. 问题描述

有n个活动申请使用同一个场所，每项活动有一个开始时间和一个截止时间，如果任何两个活动不能同时举行，问如何选择这些活动，从而使得被安排的活动数量达到最多？
设S = {1, 2, …, n}为活动的集合，si 和 fi 分别为活动i的开始和截止时间，i = 1, 2, …, n。定义活动i与j相容：si ≥ fj或sj ≥ fi, i ≠ j 求S最大的两两相容的活动子集，也即是尽可能地选择更多的会议来使用资源。

2. 算法设计(问题分析、建模、算法描述)

分析：
同一时间不能有两个活动同时发生，若（begin(1) , end(1)）区间与（begin(2) , end(2)）区间没有交集，则活动1与活动2是相容的。

描述：

1. 先把每个活动按结束时间排序，结束时间早的放在前。
2. 第一个选择活动1。
3. 从第一个开始向后依次比较选择第一个与活动1相容的活动假设为 i 。
4. 从i + 1开始向后依次遍历查找与活动i 相容的活动 j。

关键在于选择与当前活动相容的结束时间最早的活动，直到所有活动都被选择；

3. 算法源码（C++）

#include
//#define int long long

using namespace std;
const int N = 1e5 + 10;
int n;
vector< pair<int, int> > p;

bool cmp(pair<int, int> a, pair<int, int>b)
{
    return a.second <= b.second;
}

void solve()
{
    int j = 0, num = 1, a[N];
    a[0] = 1;   //选择1
    for(int i = 1; i < n; i++)
    {
        if(p[i].first >= p[j].second) //判断是否相容
        {
            a[i] = 1;
            j = i;
            num ++;
        }
        else {
            a[i] = 0;
        }
    }

    cout << "最大安排活动数量：" << num << endl;
    cout << "以下是选择的活动序号，开始、结束时间：" << endl;
    for (int i = 0; i < n; ++i) {
        if(a[i])
            cout << i + 1 << ": " << p[i].first << " " << p[i].second << endl;
    }
}

int32_t main()
{
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        int s, f;
        cin >> s >> f;
        p.push_back(make_pair(s, f));
    }

    sort(p.begin(), p.end(), cmp); //按结束时间从早到晚排序

    solve();
    return 0;
}

4. 测试数据及运算结果

测试数据选用：

i	1	2	3	4	5	6	7	8	9	10
Begin	1	3	2	5	3	5	6	8	8	2
End	4	5	6	7	8	9	10	11	12	13

输入：

10 1 4 3 5 2 6 5 7 3 8 5 9 6 10 8 11 8 12 2 13

输出：

最大安排活动数量：3
以下是选择的活动序号，开始、结束时间：
1: 1 4
4: 5 7
8: 8 11

5. 算法分析(分析算法的时间复杂度和空间复杂度)

时间复杂度：
sort排序O(nlogn) + 贪心单层循环O(n)

空间复杂度：
O(n)

---

二、最优装载问题

1. 问题描述

有一批集装箱要装上一艘载重量为 c 的轮船。其中集装箱i的重量为Wi 。最优装载问题要求确定在装载体积不受限制的情况下，将尽可能多的集装箱装上轮船。

2. 算法设计(问题分析、建模、算法描述)

分析：
这个问题相对简单，显然我们要利用 重量最轻的先装载 进行贪心选择。

先对所有物品按重量进行排序，从最轻的开始逐一放入轮船，每放一次判断一下是否超重，超重了就把最后一次放的拿出来即可。

描述：
1． 对所有物品排序，同时记录物品序号
2． 每次选择重量最轻的物品放入，然后判断是否超重
3． 重复2步骤直到超重停止
4． 处理并输出答案

3. 算法源码（C++）

#include
//#define int long long
using namespace std;
const int N = 1e5 + 10;
int n, c;
vector< pair<int, int> > p;

bool cmp(pair<int, int> a, pair<int, int>b)
{
    return a.second <= b.second;
}

void solve()
{
    int num = 0;        //装入的个数
    int tal = 0;         //装的重量总和
    vector<int> a;        //存一下装入的序号
    for(int i = 0; i < n; ++i)
    {
        tal += p[i].second;
        if(tal <= c) {
            num ++;
            a.emplace_back(p[i].first); //存序号
        }
        else {
            break;
        }
    }

    cout << "能装如最多货物的个数为：" << num << endl;
    cout << "以下是装的货物的编号：" << endl;
    for (auto ii : a) {
            cout << ii << " ";
    }
    cout << endl;
}

int main()
{
    cin >> c >> n;
    for(int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        p.push_back(make_pair(i + 1, x));   //first存序号second存重量
    }

    sort(p.begin(), p.end(), cmp); //按重量从轻到重排序

    solve();
    return 0;
}

4. 测试数据及运算结果

输入数据：

12 5 8 4 2 5 7

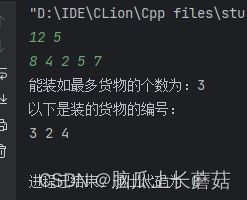
输出：

能装如最多货物的个数为：3
以下是装的货物的编号：
3 2 4

5. 算法分析(分析算法的时间复杂度和空间复杂度)

时间复杂度：
sort排序O(nlogn) + 贪心单层循环O(n)

空间复杂度：
O(n)

---

三、单源最短路问题（Dijkstra算法）

1. 问题描述

给定一个有向带权图G =(V,E)，其中每条边的权是非负实数。另外，给定V中的一个顶点，称为源点。现在要计算从源点到所有其它各顶点的最短路长度。这里路的长度是指路径上各边权之和。

2. 算法设计(问题分析、建模、算法描述)

分析：
利用Dijkstra算法思想，开一个数组S，将顶点不断加入S，每次加入代表已知了从源点到该点的最短路径长度，选择的过程即贪心的过程，不断修改答案数组dist的值直到最后所有的点都被放入S。

贪心策略：从v – s中找到具有最短特殊路长的顶点u加入S集合。

描述：

1. 创建一个集合S，将源点放入S。
2. u为某个顶点，把从源点到u且只经过集合S中的顶点的路称为源点到u的特殊路径，用数组dist记录当前每个顶点所对应的最短特殊路径长度。
3. 每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时维护数组dist。
4. 直到S包含了V中所有顶点时结束，dist数组即为最终结果。

3. 算法源码（C++）

#include 
#define INF 0x3f3f3f3f
int mp[2001][2001];
using namespace std;

int main()
{
    int num_node, num_edge;
    cout << "请输入总节点数和总边数" << endl;
    cin >> num_edge >> num_node;
    for (int i = 0; i <= num_node; i++)
    {
        for (int j = 0; j <= num_node; j++)
            mp[i][j] = INF;
    }
    for (int i = 0; i < num_edge; i++)
    {
        int st, end, length;
        cin >> st >> end >> length;
        if (mp[st][end] > length)
            mp[st][end] = length;
    }

    vector<bool> v(num_node + 1, false);        //v数组标记该结点是否已经进地杰斯特拉算法的已判断的集合，初始化为false

    vector<int> dist(num_node + 1, INF);            //dist数组记录起点到该结点的最短距离为多少，初始化为起点到各点的距离
    for (int i = 0; i <= num_node; i++)
        dist[i] = mp[1][i];
    v[1] = true;
    dist[1] = 0;
//    cout << "\n-------------------------" << endl;
//    cout << "1th" << endl;
//    for (int i = 1; i <= num_node; i++)
//    {
//        if (!v[i] && dist[i] == INF)
//            cout << i << "\tINF" << endl;
//        else if (!v[i] && dist[i] != INF)
//            cout << i << "\t" << dist[i] << endl;
//    }
    int count = 2;
    for (int i = 1; i <= num_node; i++)
    {
        int min_node = 0, mindis = INF;         // 记录当前距离最小的结点和距离
        for (int j = 1; j <= num_node; j++)     // 找到当前未标记的距离最小结点
            if (!v[j] && dist[j] < mindis)
            {
                mindis = dist[j];
                min_node = j;
            }
        if (min_node == 0)
            continue;
        v[min_node] = true;                 // 把该结点标记为已进入集合
        for (int j = 1; j <= num_node; j++)      // 更新未进入集合的结点的距离数组
        {
            if (!v[j] && dist[j] > dist[min_node] + mp[min_node][j])
                dist[j] = dist[min_node] + mp[min_node][j];
        }
//        cout << "\n-------------------------" << endl;
//        cout << count << "th" << endl;
//        count++;
//        for (int i = 1; i <= num_node; i++)
//        {
//            if (!v[i] && dist[i] == INF)
//                cout << i << "\tINF" << endl;
//            else if (!v[i] && dist[i] != INF)
//                cout << i << "\t" << dist[i] << endl;
//        }
    }
    cout << "计算结束。" << endl;
    cout << "接下来是单源最短路径的计算结果(目标点序数   从源点1到目标点的最短路径)：" << endl;

    for (int i = 1; i <= num_node; ++i) {
        cout << i << "  " << dist[i] << endl;
    }
    return 0;
}

注释部分代码可以输出每次贪心选择操作的过程，需要注意的是输入数据可能有重复边，需要存两个结点间最短的的那个。

4. 测试数据及运算结果

测试数据选用下图：

输入：

15 8 1 2 2 1 4 1 1 6 3 2 5 5 2 3 6 3 8 6 4 2 10 4 7 2 5 3 9 5 8 4 6 4
5 6 7 4 7 5 3 7 2 7 7 8 8

输出：

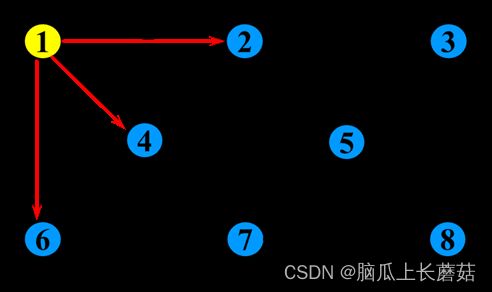
计算结束。 接下来是单源最短路径的计算结果(目标点序数 从源点1到目标点的最短路径)：
1 0
2 2
3 8
4 1
5 6
6 3
7 3
8 10

运行截图如下：

5. 算法分析(分析算法的时间复杂度和空间复杂度)

时间复杂度：
O（n²）

空间复杂度：
O（n）

总结

本章内容介绍了三种基础贪心算法的经典例题，分别是活动安排问题、最优装载问题、单源最短路问题。作为大学课程《算法设计与分析》的实验报告-贪心算法有完整的实验报告思路即格式，求赞！