堆的实现与操作

一.堆的结构

1.物理结构

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}Heap;

        堆一般用数组来存储

有两种主要类型的堆：最大堆（Max Heap）和最小堆（Min Heap）。

1. 最大堆（Max Heap）： 在最大堆中，父节点的值始终大于或等于其子节点的值。这意味着堆的根节点是具有最高优先级的元素。

2. 最小堆（Min Heap）： 在最小堆中，父节点的值始终小于或等于其子节点的值。这意味着堆的根节点是具有最低优先级的元素。

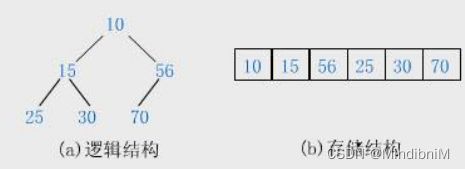
2.逻辑结构

        堆的逻辑结构是一个完全二叉树（Complete Binary Tree），这意味着除了最后一层外，其他层都是完全填充的，而且最后一层的节点都尽可能靠左排列。

类如这是一个小堆

二.堆的操作

在学习堆的操作前.我们需要学习调整算法

调整算法

1.向上调整

void AdjustUp(HPDataType* a, int child)//要调整的数组和要调整的数的下标
{
	assert(a);
	int parent = (child - 1) / 2;//找到这个数的父亲节点的下标
	while (child > 0)
	{
		if (a[child] < a[parent])//这里是实现小堆,
		{
			Swap(&a[child], &a[parent]);//交换这两个数
			child = parent;
			parent = (child - 1) / 2;//向下走
		}
		else
		{
			break;
		}
	}
}

当堆的某个节点的值发生变化，可能破坏了堆的性质（最大堆或最小堆），需要通过向上调整来修复。向上调整一般用在插入中.将这个数调整到堆里合适的位置.使得整个是一个堆

2.向下调整

void AdjustDown(HPDataType* a,int size, int panest)//要调整的数组和数组元素数和当前要调整的数下标
{
	assert(a);
	int child = panest * 2 + 1;//找到左孩子
	while (child a[child + 1])//***
		{
			child++;选取左右孩子小的那个
		}
		if (a[panest] > a[child])//***
		{
			Swap(&a[panest], &a[child]);
			panest = child;
			child = panest * 2 + 1;
		}
		else
		{
			break;
		}

	}
}

当堆的某个节点的值发生变化，可能破坏了堆的性质（最大堆或最小堆），需要通过向下调整来修复。向下调整一般用于删除

1.堆的初始化

void HeapInit(Heap* hp)
{
	assert(hp);
	hp->a = NULL;
	hp->size = 0;
	hp->capacity = 0;
}

与顺序表的初始化类似

2.堆的销毁

void HeapDestory(Heap* hp)
{
	assert(hp);
	free(hp->a);
	hp->size = 0;
	hp->capacity = 0;
}

与顺序表的销毁类似

3.堆的插入

void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	if (hp->size == hp->capacity)
	{
		int newcapacity = hp->capacity == 0 ? 10 : hp->capacity *2;
		HPDataType* arr = (HPDataType*)realloc(hp->a,sizeof(HPDataType) * newcapacity);
		if (arr == NULL)
		{
			perror("realloc:");
			exit(-1);
		}
		hp->a = arr;
		hp->capacity = newcapacity;
	}//扩容
	hp->a[hp->size++] = x;
	AdjustUp(hp->a, hp->size - 1);
}

堆的核心就是调整算法,向尾插入数据后.调整堆

4.堆的删除

void HeapPop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	Swap(&(hp->a[0]), &(hp->a[hp->size - 1]));
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);
}

堆的删除是删除堆顶数据.我们把堆顶元素和尾元素交换,然后有效数据个数减小1.在将交换到堆顶的元素向下调整

5.取堆顶数据

HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	return hp->a[0];
}

6.堆的数据个数

int HeapSize(Heap* hp)
{
	assert(hp);
	return hp->size - 1;
}

7.堆的判空

int HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->size == 0;
}

三.使用堆进行排序

1.向上调整建堆排序

void HeapSort(int* arr, int size)
{
	for (int i = 0; i < size; i++)
	{
		AdjustUp(arr, i);
	}
	int n=size-1;
	while (n>0)
	{
		Swap(&arr[0], &arr[n]);
		AdjustDown(arr, n, 0);
		n--;
	}
}

模拟堆的插入.调整数组里每一个元素建堆

每次取堆顶元素与最后一个元素交换.直至结束

2.向下调整建堆排序

void HeapSort(int* arr, int size)
{
	for (int i = (size - 1) / 2; i >= 0; i--)
		AdjustDown(arr, size, i);
	int n = size - 1;
	while (n > 0)
	{
		Swap(&arr[0], &arr[n]);
		AdjustDown(arr, n, 0);
		n--;
	}
}

从第一个非叶子节点开始调整,调整数组元素建堆,,使用局部最优达到全局最优的解法,这个方法比上一个效率更高

3.TopK问题

比如我要在1000万个数中选取最大的前K个,这时使用排序再选出就比较浪费时间,我们可以建立一个有k个元素的小堆,先将前k个建堆,

for (int i = 0; i < k; i++)
	{
		fscanf(file, "%d", &arr[i]);
		AdjustUp(arr, i);
	}

	int x;
	while (fscanf(file, "%d", &x) != EOF)
	{
		if (x > arr[0])
		{
			arr[0] = x;
			AdjustDown(arr, k, 0);
		}
	}

        这里使用了文件读取数,先建立容量为K的小堆,然后再向后面读取数,如果数更大,就入堆向下调整

直至所有数据.那么堆就是由最大K个数组成的堆.

int n = k - 1;
	while (n > 0)
	{
		Swap(&arr[0], &arr[n]);
		AdjustDown(arr, n, 0);
		n--;
	}

最后选最大数排序到后面.就找到了这K个数

时间复杂度为   O (N*log K)

近似  O(N)