数据结构第六课 -------迭代排序(快速排序和归并排序)
作者前言
✨✨✨✨✨✨
作者介绍:
作者id:老秦包你会,
简单介绍:
喜欢学习C语言和python等编程语言,是一位爱分享的博主,有兴趣的小可爱可以来互讨
个人主页::小小页面
gitee页面:秦大大
一个爱分享的小博主 欢迎小可爱们前来借鉴
迭代快速排序
- **作者前言**
- 介绍
- 归并排序
- 归并排序的非递归
介绍
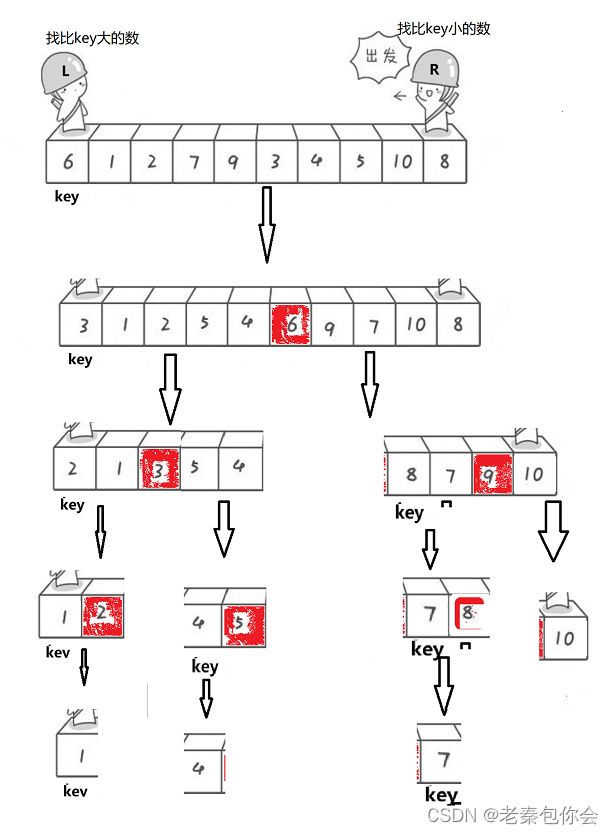
在上一篇博客中,我们使用快速排序的时候是使用递归的方式进行的,如上图所示,
但是如果我们把递归变成非递归的形式,该怎么进行呢
一般有以下方法
(1)循环 (2)借助栈
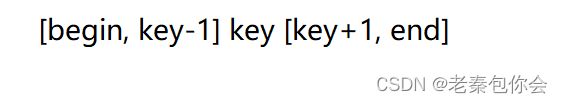
可以结合这个图进行非递归进行
这个思路图,这个图只是简单的介绍了0 ~4的栈的入栈和出栈情况
typedef int TackDataType;
typedef struct SLtack
{
TackDataType* TData;
int Top;//标识栈顶位置
int Capacity;
}SLtack;
//初始化
void TackInit(SLtack* pst)
{
assert(pst);
pst->TData = NULL;
pst->Top = 0;//栈顶元素的下一个
pst->Capacity = 0;
}
//释放
void TackDestroy(SLtack* pst)
{
assert(pst);
free(pst->TData);
pst->TData = NULL;
pst->Top = 0;
pst->Capacity = 0;
}
//插入数据
void TackPushData(SLtack* pst, TackDataType elemest)
{
assert(pst);
//判断容量
if (pst->Capacity == pst->Top)
{
TackcapacityAdd(pst);
printf("扩容成功\n");
}
assert(pst->Capacity != pst->Top);
pst->TData[pst->Top] = elemest;
pst->Top++;
}
//删除数据
void TackPopData(SLtack* pst)
{
assert(pst);
if(pst->Top)
pst->Top--;
}
//空间扩容
void TackcapacityAdd(SLtack* pst)
{
assert(pst);
//扩容
pst->Capacity = (pst->Capacity == 0 ? 4 : pst->Capacity * 2);
TackDataType* tmp = realloc(pst->TData, sizeof(TackDataType) * pst->Capacity);
if (tmp == NULL)
{
perror("realloc");
return;
}
pst->TData = tmp;
}
//找出栈顶
TackDataType TackTop(SLtack* pst)
{
assert(pst);
return *(pst->TData + (pst->Top - 1));
}
//判断栈是否为空
bool Empty(SLtack* pst)
{
assert(pst);
return pst->Top == 0;
}
//栈的长度
int TackSize(SLtack* pst)
{
assert(pst);
return pst->Top;
}
int TriNum(int* a, int begin, int end)
{
int mid = (begin - end) / 2 + end;
if (begin > end)
{
if (end > mid)
{
return end;
}
else if (begin < mid)
{
return begin;
}
return mid;
}
else
{
if (begin > mid)
{
return begin;
}
else if (end < mid)
{
return end;
}
else
return mid;
}
}
void excheng(int* a, int* b)
{
int c = *a;
*a = *b;
*b = c;
}
int main()
{
srand(time(NULL));
int N = 100;
int* arr = (int*)malloc(sizeof(int) * N);
int i = 0;
for (i = 0; i < N; i++)
{
arr[i] = rand();
}
//创建一个栈
SLtack* tack = (SLtack*)malloc(sizeof(SLtack));
//初始化
TackInit(tack);
int begin = 0;
int end = N - 1;
//插入
TackPushData(tack, begin);
TackPushData(tack, end);
while (!Empty(tack))
{
//找出栈顶
TackDataType end1 = TackTop(tack);
//删除
TackPopData(tack);
//找出栈顶
TackDataType begin1 = TackTop(tack);
//删除
TackPopData(tack);
//快速排序
int key = TriNum(arr, begin1, end1);
excheng(&arr[key], &arr[(begin1)]);
key = begin1;
int prev = begin1;
int cur = begin1 + 1;
while (cur <= end1)
{
//cur 比较
if (arr[cur] < arr[key] && ++prev != cur)//增加++prev != cur可以有效解决相同位置进行交换
{
excheng(&arr[cur], &arr[prev]);
}
cur++;
}
excheng(&arr[key], &arr[prev]);
if (begin1 < prev - 1)
{
TackPushData(tack, begin1);
TackPushData(tack, prev - 1);
}
if (prev + 1 < end1)
{
TackPushData(tack, prev + 1);
TackPushData(tack, end1);
}
}
free(arr);
TackDestroy(tack);
return 0;
}
归并排序
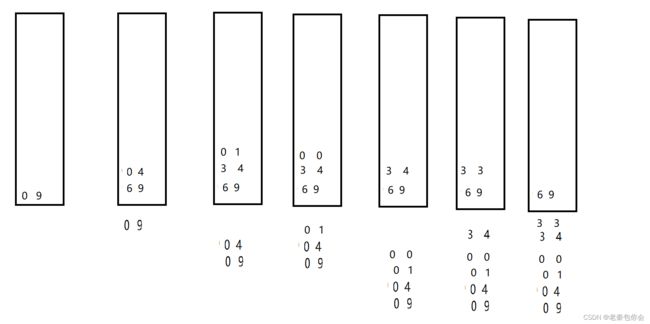
思路:
核心:分解和合并
将待排序的线性表不断地切分成若干个子表,直到每个子表只包含一个元素,这时,可以认为只包含一个元素的子表是有序表。
将子表两两合并,每合并一次,就会产生一个新的且更长的有序表,重复这一步骤,直到最后只剩下一个子表,这个子表就是排好序的线性表。
#include需要借助一个数组tmp
归并排序的非递归
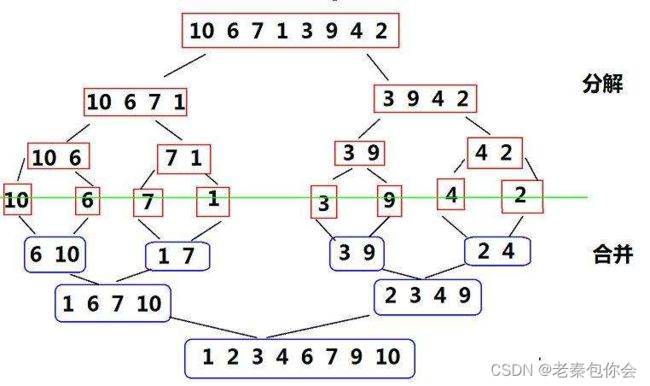
从归并排序的递归思路来,主要就是合并的思想,如果我们要把非递归的思路模拟递归的思路,就要明白归并的合并怎么开始
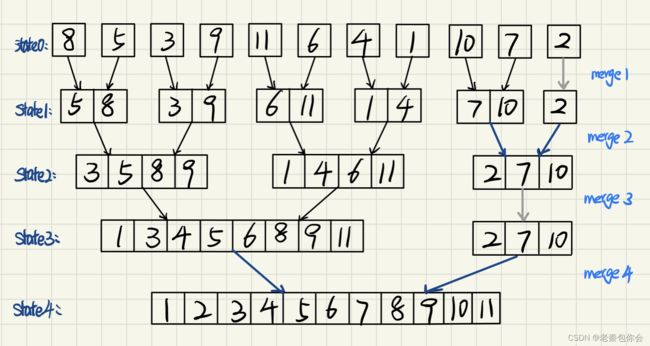
可以看出
思路:我们合并的开始是一个元素开始,第二次合并是两个元素,第三次就是4个,直到合并的长度变成了整个数组的长度,就结束
我们在两两合并的时候就是有可能会碰见落单的小数组,我们可以让其和合并过的前一个进行合并组成一个新合并的数组,
#include