《算法竞赛进阶指南》------数论习题篇1
文章目录
-
- 练习9:XOR BZOJ2115 (* 线性基。求图中异或和,可谓经典中的经典)
- 练习10:新Nim游戏 BZOJ3105 (* NIM进阶版 NIM博弈+线性基)
- 练习11:排列计数 BZOJ4517 (* 错位排序)
- 练习12: Sky Code (* 容斥原理$莫比乌斯反演 经典)
- 练习16 魔法珠 CH3B16 (SG博弈)
- 练习17:Georgia and Bob (* NIM博弈三定理)
-
- **错误思路**:
- **NIM博弈三定理**:
- **正确思路**:
练习9:XOR BZOJ2115 (* 线性基。求图中异或和,可谓经典中的经典)
传送门
题意:给一副边权非负整数的无向连通图,节点是 1 − N 1-N 1−N,问从1号节点出发,到达N号,使得路径上经过的边的权值XOR和最大。
思路:想到对图DFS,生成了一个树(怎么生成这一颗树不重要,但我们知道了1-N的路径),对于dfs中已经访问到的点还有说明能成环。能成环说明我可以走这个环也可以不走。
然后环的XOR边权值可选可不选。就可以想到用线性基.
总结: 初学线性基,很好用也很巧妙的算法实现,其思想是高斯消元。然后在这题中对图的dfs中判定环的想法学到了。这题做完有些豁然开朗。
参考博客:[学习笔记]线性基
MashiroSky
ACcode:
#include练习10:新Nim游戏 BZOJ3105 (* NIM进阶版 NIM博弈+线性基)
传送门
题意:
也就是在传统的NIM游戏中,多了一回合特殊开始。
思路:根据Nim的游戏规则,必胜则 ∑ x o r ( a [ i ] ) \sum xor(a[i]) ∑xor(a[i]), 现在我先手,我选了若干堆后。你的选择若干堆后,是希望 ∑ x o r ( a [ i ] ) = 0 \sum xor(a[i])=0 ∑xor(a[i])=0,这样你才能赢。现在对于我来说我的选择需要避免你能实现 ∑ x o r ( a [ i ] ) = 0 \sum xor(a[i])=0 ∑xor(a[i])=0。这样我才能赢。
什么情况我是必赢的呢? 我取了一部分后, ∑ x o r ( a [ i ] ) ≠ 0 \sum xor(a[i])\neq 0 ∑xor(a[i])=0,然后你无论怎么取一部分,都不能满足 ∑ x o r ( a [ i ] ) = 0 \sum xor(a[i]) = 0 ∑xor(a[i])=0。
现在的问题就变成了:我怎么取这一部分,使得原 X O R XOR XOR中任取后, ∑ X O R \sum XOR ∑XOR的线性基里不能有包含0的情况。所以我要删除若干个数,使得剩下的数的线性基不能组成0的情况。 这里的删除的数删哪呢,怎么删呢?猜一猜,推一推,贪心一下。可以得知从最小的数开始删除。
总结:NIM博弈论,线性基+贪心
ACcode:
#include练习11:排列计数 BZOJ4517 (* 错位排序)
传送门
题意:
求有多少种长度为 n n n 的序列 A A A.
满足以下条件: 1 1 1 ~ n n n 这 n n n 个数在序列中各出现了一次若第 i i i个数 A [ i ] A[i] A[i] 的值为 i i i,则称 i i i 是稳定的。序列恰好有 m m m 个数是稳定的
满足条件的序列可能很多,序列数对 10^9+7 取模。
思路:
前置知识错位排序: f ( n ) = ( f ( n − 1 ) + f ( n − 2 ) ) ∗ ( n − 1 ) f ( 1 ) = 0 , f ( 0 ) = 1 ; f(n)=(f(n-1)+f(n-2))*(n-1) f(1)=0,f(0)=1; f(n)=(f(n−1)+f(n−2))∗(n−1)f(1)=0,f(0)=1;
情况1:插入第i个元素时,前 i − 1 i-1 i−1个已经错位排好,则选择其中任意一个与第i个互换一定满足要求,选择方法共 i − 1 i-1 i−1种,前 i − 1 i-1 i−1位错排 f [ i − 1 ] f[i-1] f[i−1]种,记 f [ i − 1 ] ∗ ( i − 1 ) f[i-1] * (i-1) f[i−1]∗(i−1)
情况2:插入第i个元素时,前 i − 1 i-1 i−1个中恰有一个元素 a [ j ] a[j] a[j]使得 a [ j ] = j a[j]=j a[j]=j,其他i-2个错位排好,则将 i i i与 j j j交换, j j j在 i − 2 i-2 i−2位中的插入共 i − 1 i-1 i−1种,前i-2位错排f[i-2]种,记 f [ i − 2 ] ∗ ( i − 1 ) f[i-2]*(i-1) f[i−2]∗(i−1)
ACcode
#include
return ;
}
ll C(ll n,ll m){
if(n<m) return 0;
// printf("%d %d %d\n",a[n],inv[m],inv[n-m]);
return (a[n]*qpow(a[m],P-2)%P *qpow(a[n-m],P-2))%P;
}
void solve(){
// printf("%d %d\n",qpow(2,10),C(6,2));
ll n,m;
n=read();
m=read();
ll sum=C(n,m)*f[n-m]%P;
printf("%lld\n",sum);
return ;
}
int main (){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
pre();
int T=read();
while(T--)
solve();
getchar();
getchar();
return 0;
}
练习12: Sky Code (* 容斥原理$莫比乌斯反演 经典)
题意: 给 N N N个数,求解 g c d ( a , b , c , d ) = = 1 gcd(a,b,c,d)==1 gcd(a,b,c,d)==1 的个数有多少。
思路: 容斥原理,经典中的经典。正面求解困难,求相反问题,四元数不互质的个数是多,然后 总 数 − 它 总数-它 总数−它。
考虑不互质的情况。当我们得出了 d = 2 , d = 3 d=2,d=3 d=2,d=3的个数,那么在 d = 6 d=6 d=6时会重复,所以要减去。
总结: 莫比乌斯反演与容斥原理
ACcode
#include练习16 魔法珠 CH3B16 (SG博弈)
// submitted by HNUST26
#include
return i;
}
}
}
void solve(){
int n;
memset(a,-1,sizeof(a));
a[1]=0;
while(scanf("%d",&n)!=EOF){
int ans=0;
rep(i,1,n){
ans^=dfs(read());
}
if(ans==0) cout<<"rainbow"<<endl;
else cout<<"freda"<<endl;
}
return ;
}
int main (){
// freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
solve();
getchar();
getchar();
return 0;
}
练习17:Georgia and Bob (* NIM博弈三定理)
题意:排成直线的格子上放有 n n n个棋子。棋子i在左数第 p i p_i pi的格子上, G e o r g i a Georgia Georgia 和 B o b Bob Bob轮流选择一个棋子向左移动,每次可以移动一格及任意多格,但是不允许反超其他的棋子,也不允许将两个棋子凡在同一个格子内。无法移动操作的一方失败。Georgia 先移动。
思路:
错误思路:
我最先想到的思路是,排个序, a [ i ] a[i] a[i]的棋子最终在 i i i的位置,具体实现如下:
for(int i=1;i<=n;i++){
sum^=(a[i]-left-1);
left++;
}
当时WA了,我恨不能理解为什么。于是我返过头又看了看NIM博弈的原理是什么呢?
NIM博弈三定理:

大概就是我要胜出的话,我需要抛出a1^ a2 ^ a3…^an=0给对方。那就是原理2了。所以呢,要满足NIM博弈还有一个要求的满足的条件是
每一推都要独立,不能受到影响。 而我在写的代码思路中,是一堆一堆石子取完,再取下一堆石子。而NIM博弈中我可以去一部分第一堆的石子,而后下一步可以从第二堆里去一部分石子。所以我的博弈想法出现了每一堆石子出现的先后的取,有影响。所以思路错误。
正确思路:

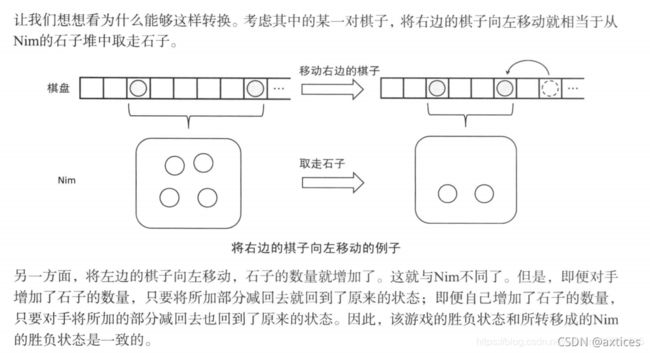
而这里"只要将所加部分减回去就回到了原来的状态"。我的理解是我的博弈状态还是希望对方面临的异或和是0,我就能胜利。所以我并不想打破这种我能"胜利的局面",所以在原基础上我再减就好了。(有点像"敌不动,我不动",hmm我举的比喻,还算清楚吗?),所以在这里可以把他们看成一对一对的来处理,每一堆的石子是并没有影响的,就是独立的喽。
总结: 在做博弈论的题目时,先理清题意的要求,在使用结论时,始终依NIM博弈的三定理为依据且在策略中不能违背。
ACcode:
#include未完待续,持续更新中…
