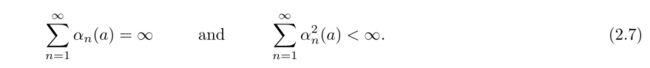RL_第二章学习笔记
笔记用 。。。
参考了很多大手的博客,简书,
第一次写博客,不知道怎么编排,很多地方都是截图的Typora
欢迎阅读,批评,指正。
也有很多地方没有理解,希望可以有大手留言,也可以留联系方式一起交流、进步。。。
编程在学后续可能会更新。
Part-one: Tabular Solution Methods
Second chapter: 多臂老虎机(Multi-armed Bandits)
强化学习与其他学习方式区分的最重要特征是它利用训练信息评估动作而不是给定矫正动作进行指导。这就需要对良好行为的积极探索。纯粹的反馈评估意味着只能得知采取动作的好坏,却不能评估是否是最佳或最坏的动作。另一方面,纯粹的反馈指导指明了所要采取的正确动作,与我们实际采取的动作无关。这类反馈是监督学习包括一大部分模式识别、人工神经网络、系统识别的基础。这两种反馈的纯粹形式有很明显的区别:反馈评估完全依赖所采取的动作,而反馈指导与之独立。
2.1 K臂老虎机
Environment:假设面临K个摇臂,重复性进行动作选取,每选取一个摇臂获得一个随机奖励值,每个摇臂之间获取随机奖励的概率固定且不尽相同。
Goal:最大化一段时间内预期的奖励值。
greedy actions:利用(exploit)当前的认知选择奖励最多的动作
nongreedy actions:探索(explore)未知动作
2.2 动作值方法(Action-value Methods)
Defination: 估计动作的价值,利用估计进行动作决策
Method(样本均值估计法):
greedy action:在一个或多个最高奖励估计的动作中进行随机挑选
ϵ-greedy methods
Defination:在绝大多数时间下,选择贪婪动作,而在一些随机时间里(比如概率为 ϵ 的情况下)随机选择一个动作
Advantage:随着执行步数的持续增加,每一个动作被执行的次数也将接近无限,保证了Q收敛于q。
question:
如果有两个动作,其中贪心概率ϵ=0.5,那么贪心动作被选择的概率为:
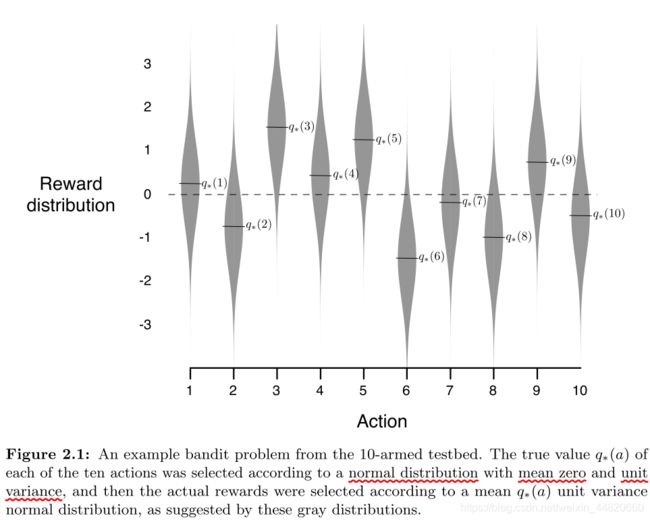
2.3十臂实验(The 10-armed Testbed)
Example:
为了比较 greedy方法 和 ϵ-greedy方法,引用了这样一个例子:样本数为 2000 的 kkk-armed bandit problem,其中k=10。每一个动作的 value q满足均值为0、方差为1的高斯分布,进而每一步的回报 R满足均值为 q方差为1的高斯分布。
greedy:奖励低,且最优行为利用低。
ϵ-greedy:奖励高,最优行为利用高。
ϵ=0.1:优先找到最优动作,但未利用时间也会增加(超过91%)
ϵ=0.01:找到最优动作耗时长,但最终效果会比 ϵ=0.1好
解决方案:可以让ϵ逐渐减小实现高速探索、高奖励值。
Summary:
ϵ-greedy 会在方差越大的情况下效果越好,当方差为0时greedy或许效果最好,因为省去了exploration,它知道每一步的真实value。但是在RL中即使任务是固定的、确定性的,也需要进行良好的平衡between exploration and exploitation。
Question:
2.4增量式实施
Prior computation-formulation:
为简化概念,这里我们只关注一个action,假设 R i R_i Ri是第 i 次选择这个action所获得的reward, Q n 代 表 这 个 动 作 被 中 n − 1 次 的 e s t i m a t e − v a l u e 其 表 达 式 为 : Q_n代表这个动作被中n-1次的 estimate-value 其表达式为: Qn代表这个动作被中n−1次的estimate−value其表达式为:
shortcoming
将所有的历史信息全部记录下来然后求平均,如果历史记忆很长,甚至无限,那么直接求解将受到内存和运行时间的限制。
Incremental formulas:
将所有历史信息记录下来是没有必要的,我们完全可以采用下列公式:
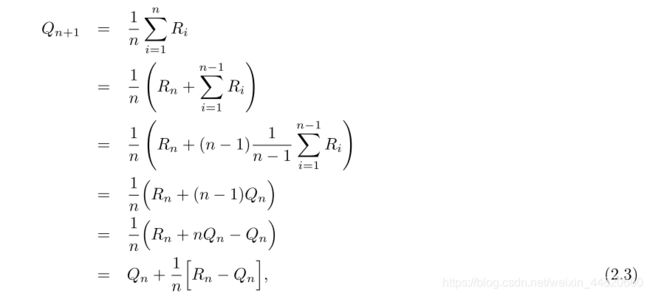
每次只需要存储 Q n 和 n Q_n和n Qn和n就可以算出新的reward。 其中1/n为步长参数,本书中我们以α或者更普遍的 α t ( a ) α_t(a) αt(a)来代替(因为最终求取的是估计值的最优)。
General form:
Advantage:
耗费固定大小的内存,且可以单步更新。
Pseudocode:
第二步:循环:
(1)以ϵ-greedy策略选取动作
(2)动作选择记录奖励值
(3)次数+1
(4)增量式计算estimate value
2.5 跟踪非稳定性问题:
weighted average(加权平均值):
事实上,我们碰到的问题多是非稳定性的问题(其动作值不符合一定的分布),在这种情况下,对最近的奖励给予更多的重视比对过去的奖励给予更多的重视将更有意义。一种最流行的做法是将步长参数设为一个常数,将incremental formulation改写为:
Converging condition:
α_n(a)表示在第n步选择动作a后获得的回报的step-size参数。
第一个条件要求steps足够大从而克服任何初始条件和随机波动的影响;
第二个条件要求steps变得越来越小从而能保证收敛性。
上一节样本均值法中 α n ( a ) = 1 / n α_n(a)=1/n αn(a)=1/n,满足收敛,而 α n ( a ) = α α_n(a)=α αn(a)=α只满足前一种条件。
Essential:
事实上,对于非稳定性环境,更需要不收敛的特性,对最新的奖励(不断变动)进行反应,而且符合收敛条件的step-size parameters收敛过程是非常缓慢的,需要不断进行调整。一般只用于理论工作,极少应用到实际。
Summary:
Question:
2.6 Optimistic Initial Values
偏差存在:
实际上这种偏差不是问题,反而肯会有非常有用,好处是它提供了一种简单的方式来传达可以预期的奖励水平的先验知识。坏处是它是一组必须由用户选择的参数,如果初始值全部为0的话。
Comparison:
Advantage:
最初,Optimistic Initial Values Method表现更差,因为它探索更多,但最终它表现更好,因为它的探索随着时间的推移而减少, 它是一个简单的技巧,对于静止问题非常有效 。
Disadvantage:
它远不是一个鼓励探索的普遍有用的方法。 例如,它不适合非平稳问题,因为它的驱动对于探索本质上是暂时的。 如果任务发生变化,再次需要探索,这种方法无法帮助。
Summary:
实际上,任何以特殊方式关注初始条件的方法都不可能对一般的非平稳情况有所帮助。 时间的开始只出现一次,因此我们不应该过分关注它 ,样本均值法同样如此。 也将时间的开始视为一种特殊的方法事件,平均所有后续奖励的权重相等。
Questions:
2.7 上限置信区间动作选择(Upper-Confidence-Bound Action Selection)
Why:
学习过程中,探索是必要的行动,因为action-value-estimate的准确性始终存在不确定性,greedy actions只代表当前的最优动作,ϵ-greedy尝试non-greedy action,但没有尝试不确定性以及近似贪婪动作。
最好的方法是根据它们的实际最优潜力来选择non-greedy action,同时考虑他们的估计与最大值的接近程度以及这些估计中的不确定性:
Fundamental:
Comparison:UCB and ϵ-greedy
Advantage:
如本文所示,比较ϵ-greedy方法,UCB通常表现良好 。
Shortcoming:
UCB更难向本书其余部分所考虑的更为普遍的强化学习环境扩展。 一个难点在于处理非平稳问题; 另一个难点是处理大的状态空间,特别是当使用本书第二部分中开发的函数逼近时。 在这些更高级的设置中,UCB动作选择的想法通常是不实际的。
Summary
初始每一个arm被选中一次, 均值越大,标准差越小,被选中的概率会越来越大。被选次数较少的臂虽然可能均值不大,但根号那一项会比较大,也会得到试验机会。
Question:

10个摇臂全部测试后选择一个greedy-action????获得较高奖励????但为什么会有较大峰值不理解 感觉具有偶然性,因为奖励具有随机。
2.8 Gradient Bandit Algorithms
soft-max distribution(Gibbs or Boltzmann distribution):
Action preferences Algorithm:
Comparison:
10-臂赌博机变体实验,选定预期奖励为均值为+4而不是0的正态分布,方差仍为1。将baseline设为0对比梯度赌博机算法的结果 :

The derivation process:
Question:
2.9 关联搜索(Associative Search ):
本章中我们只考虑了非关联性任务,即不需要将不同行为与不同情况联系起来。 但是,在一般的强化学习任务中,存在多种情况。我们的目标是获得一个策略:这些情况下最佳的行为的映射 。 如果允许行动来影响下一个情况以及奖励,那么我们就会有完整的强化学习问题。
2.10 Summary:
对比展示针对本章中各种赌博机算法的度量,每种度量都是其自身参数的函数,在x轴上以单个比例显示:
Question:
参考:
https://www.jianshu.com/p/efb723420ee6
https://blog.csdn.net/zte10096334/article/details/83446191