树上计数2 树上莫队

原题
给定一棵 N 个节点的树，节点编号从 1 到 N，每个节点都有一个整数权值。

现在，我们要进行 M 次询问，格式为 u v，对于每个询问你需要回答从 u 到 v 的路径上（包括两端点）共有多少种不同的点权值。

输入格式
第一行包含两个整数 N,M。

第二行包含 N 个整数，其中第 i 个整数表示点 i 的权值。

接下来 N−1 行，每行包含两个整数 x,y，表示点 x 和点 y 之间存在一条边。

最后 M 行，每行包含两个整数 u,v，表示一个询问。

输出格式
共 M 行，每行输出一个询问的答案。

数据范围
1≤N≤40000,
1≤M≤105,
1≤x,y,u,v≤N,
各点权值均在 int 范围内。

输入样例：
8 2
105 2 9 3 8 5 7 7
1 2
1 3
1 4
3 5
3 6
3 7
4 8
2 5
3 8
输出样例：
4
4

首先引入几个定理：
以欧拉序遍历树，生成一个欧拉序数组。设first[x]是x第一次出现的位置,last[x]是x最后一个出现的位置，那么针对询问x,y的路径上有多少不同权值:
特殊情况：若x是x与y的最近公共祖先(lca)，那么就是在欧拉序数组中下标从first[x]到first[y]中出现的所有数中只出现过一次的数
一般情况:last[x]到first[y]中出现一次的数，并且再加上他们的最近公共祖先
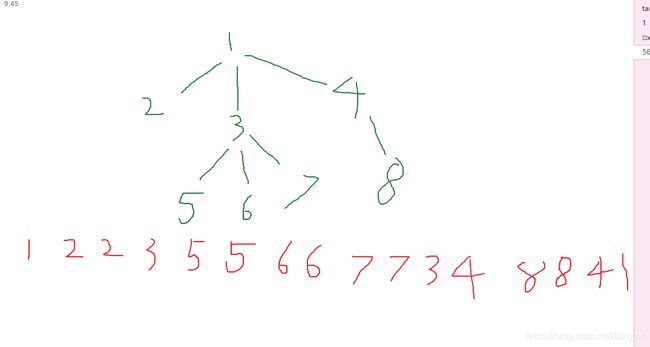
如图，就是一个树和它的欧拉序数组
比如询问1号点到5号点。1号点的first下标为1，5的first下标为5，在欧拉序数组中有1 2 2 3 5 只出现过一次的只有1 3 5，就是答案。
询问 5号点到 8号点，5 的last下标为6，8的first是13，中间有 5 66 77 3 4 8
只出现一次的有 5 3 4 8，然后再加上他们的最近公共祖先1，就是5 3 1 4 8
这样就把树上询问转换成区间询问，之后再用经典莫队处理就好

以下就是代码+注释

#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

const int N = 100010;

int n, m, len;
int w[N];
int h[N], e[N], ne[N], idx;
int depth[N], f[N][16];
int seq[N], top, first[N], last[N];
int cnt[N], st[N], ans[N];
int que[N];
struct Query
{
    int id, l, r, p;
}q[N];
vector<int> nums;

void add_edge(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u, int father)
{
    seq[ ++ top] = u;
    first[u] = top;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j != father) dfs(j, u);
    }
    seq[ ++ top] = u;
    last[u] = top;
}

void bfs()
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[1] = 1;
    int hh = 0, tt = 0;
    que[0] = 1;
    while (hh <= tt)
    {
        int t = que[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (depth[j] > depth[t] + 1)
            {
                depth[j] = depth[t] + 1;
                f[j][0] = t;
                for (int k = 1; k <= 15; k ++ )
                    f[j][k] = f[f[j][k - 1]][k - 1];
                que[ ++ tt] = j;
            }
        }
    }
}

int lca(int a, int b)
{
    if (depth[a] < depth[b]) swap(a, b);
    for (int k = 15; k >= 0; k -- )
        if (depth[f[a][k]] >= depth[b])
            a = f[a][k];
    if (a == b) return a;
    for (int k = 15; k >= 0; k -- )
        if (f[a][k] != f[b][k])
        {
            a = f[a][k];
            b = f[b][k];
        }
    return f[a][0];
}

int get(int x)
{
    return x / len;
}

bool cmp(const Query& a, const Query& b)
{
    int i = get(a.l), j = get(b.l);
    if (i != j) return i < j;
    return a.r < b.r;
}

void add(int x, int& res)
{
    st[x] ^= 1;
    if (st[x] == 0)
    {
        cnt[w[x]] -- ;
        if (!cnt[w[x]]) res -- ;
    }
    else
    {
        if (!cnt[w[x]]) res ++ ;
        cnt[w[x]] ++ ;
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]), nums.push_back(w[i]);
    sort(nums.begin(), nums.end());
    nums.erase(unique(nums.begin(), nums.end()), nums.end());
    for (int i = 1; i <= n; i ++ )
        w[i] = lower_bound(nums.begin(), nums.end(), w[i]) - nums.begin();

    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add_edge(a, b), add_edge(b, a);
    }

    dfs(1, -1);
    bfs();

    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        if (first[a] > first[b]) swap(a, b);
        int p = lca(a, b);
        if (a == p) q[i] = {i, first[a], first[b]};
        else q[i] = {i, last[a], first[b], p};
    }

    len = sqrt(top);
    sort(q, q + m, cmp);

    for (int i = 0, L = 1, R = 0, res = 0; i < m; i ++ )
    {
        int id = q[i].id, l = q[i].l, r = q[i].r, p = q[i].p;
        while (R < r) add(seq[ ++ R], res);
        while (R > r) add(seq[R -- ], res);
        while (L < l) add(seq[L ++ ], res);
        while (L > l) add(seq[ -- L], res);
        if (p) add(p, res);
        ans[id] = res;
        if (p) add(p, res);
    }

    for (int i = 0; i < m; i ++ ) printf("%d\n", ans[i]);

    return 0;
}