【数据结构和算法】到达首都的最少油耗
其他系列文章导航
Java基础合集
数据结构与算法合集设计模式合集
多线程合集
分布式合集
ES合集
文章目录
其他系列文章导航
文章目录
前言
一、题目描述
二、题解
三、代码
四、复杂度分析
前言
这是力扣的2477题,难度为中等,解题方案有很多种,本文讲解我认为最奇妙的一种。
一、题目描述
给你一棵 n 个节点的树(一个无向、连通、无环图),每个节点表示一个城市,编号从 0 到 n - 1 ,且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ,其中 roads[i] = [ai, bi] ,表示城市 ai 和 bi 之间有一条 双向路 。
每个城市里有一个代表,他们都要去首都参加一个会议。
每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目。
城市里的代表可以选择乘坐所在城市的车,或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。
请你返回到达首都最少需要多少升汽油。
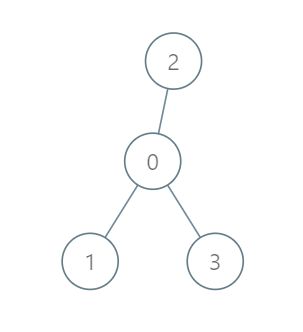
示例 1:
输入:roads = [[0,1],[0,2],[0,3]], seats = 5 输出:3 解释: - 代表 1 直接到达首都,消耗 1 升汽油。 - 代表 2 直接到达首都,消耗 1 升汽油。 - 代表 3 直接到达首都,消耗 1 升汽油。 最少消耗 3 升汽油。
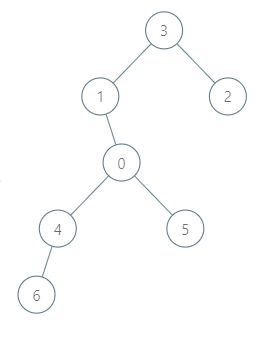
示例 2:
输入:roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2 输出:7 解释: - 代表 2 到达城市 3 ,消耗 1 升汽油。 - 代表 2 和代表 3 一起到达城市 1 ,消耗 1 升汽油。 - 代表 2 和代表 3 一起到达首都,消耗 1 升汽油。 - 代表 1 直接到达首都,消耗 1 升汽油。 - 代表 5 直接到达首都,消耗 1 升汽油。 - 代表 6 到达城市 4 ,消耗 1 升汽油。 - 代表 4 和代表 6 一起到达首都,消耗 1 升汽油。 最少消耗 7 升汽油。
示例 3:
输入:roads = [], seats = 1 输出:0 解释:没有代表需要从别的城市到达首都。
提示:
1 <= n <= 105roads.length == n - 1roads[i].length == 20 <= ai, bi < nai != biroads表示一棵合法的树。1 <= seats <= 105
二、题解
本题用的贪心 + DFS解题。
这道题其实是要找到 树结构中所有节点到根节点的最小开销和 。
题目中的每个城市其实就是树结构中的一个节点,除了根节点外,每个节点都要从自身出发到达根节点,这其实就是根节点到每个节点的路径。【深度优先搜索先准备着】
每个节点之间一辆车的转移的开销为 1,我们要让开销和最小,那么就要使每个节点之间的转移车尽量的少。
那么怎么安排每个节点之间转移的车辆数呢,我们可以统计途径每个节点的代表人数有多少个,这些代表从当前节点往根节点方向转移到下一个节点【树结构,只有一种转移方式】需要车辆数,一定是 代表人数除以车的容量然后向上取整。
经过每个节点的代表人数就 是以这个节点为根的子树的节点数 , 我们可以通过深度优先搜索递归处理时, 返回当前节点为根的子树的节点数。
注意:
通过向下取整得到向上取整的策略:
本文用的是Math.ceil()方法,或者你也可以使用 (m + n - 1) / n,原理就不推导了。
根节点不转移:
深度优先搜索的递归中, 对城市 0, 其没有要转移的下一个节点, 因此不能计算转移消耗的汽油数。
三、代码
Java版本:
class Solution {
//测试代码
public static void main(String[] args) {
int[][] roads = {{0, 1}, {0, 2}, {0, 3}};
int seats = 5;
long fuel = minimumFuelCost(roads, seats);
System.out.println(fuel);
}
private static long fuel = 0;//耗油量
public static long minimumFuelCost(int[][] roads, int seats) {
int n = roads.length + 1;
List> tree = new ArrayList<>();//生成树结构
for (int i = 0; i < n; i++) {
tree.add(new ArrayList<>());
}
for (int[] r : roads) {//把每个国家的邻居存入小list,本国是大list,例如{{123}},代表0国,邻国123
tree.get(r[0]).add(r[1]);
tree.get(r[1]).add(r[0]);
}
boolean[] visited = new boolean[n];//标记城市是否遍历
visited[0] = true;//初始标记首都已遍历
dfs(0, tree, visited, seats);//从0节点开始深度优先搜索寻找每一条路径
return fuel;
}
private static int dfs(int city, List> tree, boolean[] visited, int seats) {
int people = 1;//每座城市初始一个代表
for (int neighbor : tree.get(city)) {//遍历邻国
if (!visited[neighbor]) {
visited[neighbor] = true;//标记遍历成功
people += dfs(neighbor, tree, visited, seats);// 累加到达当前城市的代表人数
}
}
if (city != 0) {// city 不为 0 ,就需要在移动到下一个节点,people 个代表需要的车辆数等于 people ÷ seats 向上取整
fuel += Math.ceil((double) people / seats);//每辆车消耗1汽油
}
return people;
}
} C++版本:
class Solution {
public:
long long minimumFuelCost(vector>& roads, int seats) {
int n = roads.size() + 1;
vector g[n];
for (auto& e : roads) {
int a = e[0], b = e[1];
g[a].emplace_back(b);
g[b].emplace_back(a);
}
long long ans = 0;
function dfs = [&](int a, int fa) {
int sz = 1;
for (int b : g[a]) {
if (b != fa) {
int t = dfs(b, a);
ans += (t + seats - 1) / seats;
sz += t;
}
}
return sz;
};
dfs(0, -1);
return ans;
}
};
Python3版本:
class Solution:
def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:
def dfs(a: int, fa: int) -> int:
nonlocal ans
sz = 1
for b in g[a]:
if b != fa:
t = dfs(b, a)
ans += ceil(t / seats)
sz += t
return sz
g = defaultdict(list)
for a, b in roads:
g[a].append(b)
g[b].append(a)
ans = 0
dfs(0, -1)
return ans
四、复杂度分析
时间复杂度 O(n),空间复杂度 O(n)。其中 n 为节点数。