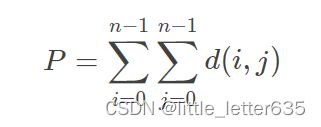NEUQ-ACM预备队训练-week11

T1.P1796 汤姆斯的天堂梦

洛谷原题

题目描述

汤姆斯生活在一个等级为 0 的星球上。那里的环境极其恶劣，每天 12 小时的工作和成堆的垃圾让人忍无可忍。他向往着等级为 N 的星球上天堂般的生活。

有一些航班将人从低等级的星球送上高一级的星球，有时需要向驾驶员支付一定金额的费用，有时却又可以得到一定的金钱。

汤姆斯预先知道了从 0 等级星球去 N 等级星球所有的航线和需要支付（或者可以得到）的金钱，他想寻找一条价格最低（甚至获得金钱最多）的航线。

输入格式

第一行一个正整数 N（N≤100），接下来的数据可分为 N 个段落，每段的第一行一个整数 Ki​（Ki​≤100），表示等级为 i 的星球有 Ki​ 个。

接下来的 Ki​ 行中第 j 行依次表示与等级为 i，编号为 j 的星球相连的等级为 i−1 的星球的编号和此航线需要的费用（正数表示支出，负数表示收益，费用的绝对值不超过 1000）。

每行以 0 结束，每行的航线数 ≤100。

输出格式

输出所需（或所得）费用。正数表示支出，负数表示收益。

输入输出样例

输入

3
2
1 15 0
1 5 0
3
1 -5 2 10 0
1 3 0
2 40 0
2
1 1 2 5 3 -5 0
2 -19 3 -20 0

输出

-1

说明/提示

对于 100% 的数据 1≤N≤100，1≤Ki​≤100。

样例解释：

 比较简单的一道DP题，从小到大对每个星球从所有路径中选择最省钱的那一条路，一直到最高等级的行星，最后在最高等级行星里面选出花钱最少甚至赚钱的那一条路，输出即可

#include 
using namespace std;

int main() {
	int k, n;
	cin >> k;
	int f[105][105];
	for (int i = 1; i < 105; i++) {
		for (int j = 1; j < 105; j++) {
			f[i][j] = 2000000000;
		}
	}
	for (int i = 1; i <= k; i++) {
		cin >> n;
		for (int l = 1; l <= n; l++) {
			int j;
			cin >> j;
			while (j) {
				int m;
				cin >> m;
				f[i][l] = min(f[i][l], f[i - 1][j] + m);
				cin >> j;
			}
		}
	}
	int ans = 2000000000;
	for (int i = 1; i <= n; i++) {
		ans = min(ans, f[k][i]);
	}
	cout << ans;
	return 0;
}

T2.P1806 跑步

洛谷原题

题目描述

路人甲准备跑 n 圈来锻炼自己的身体，他准备分多次（>1）跑完，每次都跑正整数圈，然后休息下再继续跑。

为了有效地提高自己的体能，他决定每次跑的圈数都必须比上次跑的多。

可以假设他刚开始跑了 0 圈，那么请问他可以有多少种跑完这 n 圈的方案？

输入格式

一行一个整数，代表 n。

输出格式

一个整数表示跑完这 n 圈的方案数。

输入输出样例

输入

212

输出

995645335

说明/提示

数据规模与约定

对于 100% 的数据，保证 5≤n≤500。

也是一道DP题，如果用二维数组来求的话可以直接用f[i][j]来表示总共跑了i圈最后一次跑了j圈的情况，转移方程也很好写，就是f[i][j] += f[i-j][k]，之后换一下计算的顺序，把他变成一维数组，每次算完f[i]之后把后面所有大于i的值更新一下，算到最后就是需要求的值了

#include 
using namespace std;

int main() {
	int n;
	cin >> n;
	long long f[505] = {1};
	for (int i = 1; i <= n; i++) {
		for (int j = n; j >= i; j--) {
			f[j] += f[j - i];
		}
	}
	cout << f[n] - 1;
	return 0;
}

T3.P8742 [蓝桥杯 2021 省 AB] 砝码称重

洛谷原题

题目描述

你有一架天平和 N 个砝码, 这 N 个砝码重量依次是 W1​,W2​,⋯,WN​ 。 请你计算一共可以称出多少种不同的重量?

注意砝码可以放在天平两边。

输入格式

输入的第一行包含一个整数 N。

第二行包含 N 个整数: W1​,W2​,W3​,⋯,WN​ 。

输出格式

输出一个整数代表答案。

输入输出样例

输入 #1复制

3
1 4 6

输出 #1复制

10

说明/提示

【样例说明】

能称出的 10 种重量是: 1 、 2 、 3 、 4 、 5 、 6 、 7 、 9 、 10 、 11

 

【评测用例规模与约定】

对于所有评测用例, 1≤N≤100,N 个砝码总重不超过 10^5。

问能有几种不同的摆法，用一个数组f[i]来表示重量为i是否可以称出来，能则f[i]=1，不能则f[i]=0，然后对每一个砝码Wn，遍历一遍数组，如果f[i]为1，则f[i-Wn]和f[i+Wn]应该也为1，当对每一个砝码处理完成之后，再次遍历这个数组，计数，输出答案即可

#include 
#include 
#include 
using namespace std;
#define p 100005

int n, ans = 0, sum = 0;

int w[105] = {0};

bool we[105][100005] = {false};

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> w[i];
		sum += w[i];
	}
	for (int i = 1; i <= n; i++) {
		for (int j = sum; j > 0; j--) {
			we[i][j] = we[i - 1][j] || we[i - 1][j + w[i]] || we[i - 1][abs(j - w[i])];
			if (j == w[i])
				we[i][j] = true;
		}
	}
	for (int i = 1; i <= sum; i++) {
		ans += we[n][i];
	}
	cout << ans;
	return 0;
}

T4.P1959 遗址

洛谷原题

题目描述

很久很久以前有一座寺庙，从上往下看寺庙的形状正好是一个正方形，由 4 个角上竖立的圆柱搭建而成。现在圆柱都倒塌了，只在地上留下圆形的痕迹，可是现在地上有很多这样的痕迹，专家说一定是最大的那个。

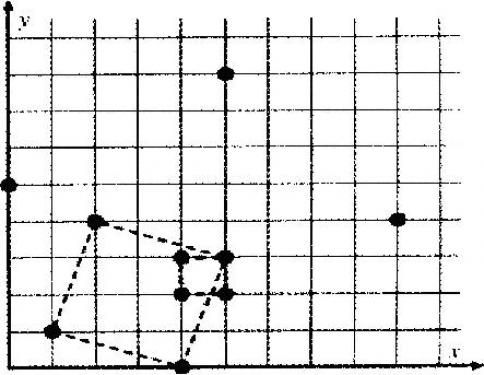
写一个程序，给出圆柱的坐标，找出由 4 个圆柱构成的最大的正方形，因为这就是寺庙的位置，要求计算出最大的面积。注意正方形的边不一定平行于坐标轴。

例如图有 10 根柱子，其中 (4,2),(5,2),(5,3),(4,3) 可以形成一个正方形，(1,1),(4,0),(5,3),(2,4) 也可以，后者是其中最大的，面积为 10。

输入格式

第一行包含一个 N(1≤N≤3000)，表示柱子的数量。

接下来 N 行，每行有两个空格隔开的整数表示柱子的坐标（坐标值在 0 到 5000 之间），柱子的位置互不相同。

输出格式

如果存在正方形，输出最大的面积，否则输出 0。

输入输出样例

输入 #1复制

 10
 9 4
 4 3
 1 1
 4 2
 2 4
 5 8
 4 0
 5 3
 0 5
 5 2

输出 #1复制

10

说明/提示

【数据范围】

100% 满足：1≤N≤3000。

从一堆柱子里面寻找能构成的最大正方体，这道题的核心就是寻找正方体了，如果对每四个点比较看是否可以构成正方体肯定是不行的，我们可以用另一种方法，对每两个点进行检查，因为在平面里，如果四个点可以构成正方形，当我们确定了两个点之后另外两个点只有两种情况，我们对每两个点检查它的左边和右边的相应位置是否有柱子，如果有则代表这个地方可以构成正方体，然后进行比较，寻找最大值，最后输出

#include 
using namespace std;
int point[2][3005];

bool map[5005][5005] = {0};


int main() {
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> point[0][i] >> point[1][i];
		map[point[0][i]][point[1][i]] = true;
	}
	int ans = 0;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (i == j)
				continue;
			int ax, ay, bx, by;
			int x = point[1][i] - point[1][j];
			int y = point[0][i] - point[0][j];
			ax = point[0][i] - x;
			ay = point[1][i] + y;
			bx = point[0][j] - x;
			by = point[1][j] + y;
			if (ax < 1 || ax > 5000 || bx < 1 || bx > 5000 || ay < 1 || ay > 5000 || by < 1 || by > 5000)
				continue;
			if (map[ax][ay] && map[bx][by]) {
				ans = max(ans, x * x + y * y);
			}
		}
	}
	cout << ans << endl;
	return 0;
}

 T5.P8794 [蓝桥杯 2022 国 A] 环境治理

题目描述

LQ 国拥有 n 个城市，从 0 到 n−1 编号，这 n 个城市两两之间都有且仅有一条双向道路连接，这意味着任意两个城市之间都是可达的。每条道路都有一个属性 D，表示这条道路的灰尘度。当从一个城市 A 前往另一个城市 B 时，可能存在多条路线，每条路线的灰尘度定义为这条路线所经过的所有道路的灰尘度之和，LQ 国的人都很讨厌灰尘，所以他们总会优先选择灰尘度最小的路线。

LQ 国很看重居民的出行环境，他们用一个指标 P 来衡量 LQ 国的出行环境，P 定义为：

 

其中 d(i,j) 表示城市 i 到城市 j 之间灰尘度最小的路线对应的灰尘度的值。

为了改善出行环境，每个城市都要有所作为，当某个城市进行道路改善时，会将与这个城市直接相连的所有道路的灰尘度都减少 1，但每条道路都有一个灰尘度的下限值 L，当灰尘度达到道路的下限值时，无论再怎么改善，道路的灰尘度也不会再减小了。

具体的计划是这样的：

• 第 1 天，0 号城市对与其直接相连的道路环境进行改善；
• 第 2 天，1 号城市对与其直接相连的道路环境进行改善；

……

• 第 n 天，n−1 号城市对与其直接相连的道路环境进行改善；
• 第 n+1 天，0 号城市对与其直接相连的道路环境进行改善；
• 第 n+2 天，1 号城市对与其直接相连的道路环境进行改善；

……

LQ 国想要使得 P 指标满足 P≤Q。请问最少要经过多少天之后，P 指标可以满足 P≤Q。如果在初始时就已经满足条件，则输出 0；如果永远不可能满足，则输出 −1。

输入格式

输入的第一行包含两个整数 n,Q，用一个空格分隔，分别表示城市个数和期望达到的 P 指标。

接下来 n 行，每行包含 n 个整数，相邻两个整数之间用一个空格分隔，其中第 i 行第 j 列的值 Di,j​(Di,j​=Dj,i​,Di,i​=0) 表示城市 i 与城市 j 之间直接相连的那条道路的灰尘度。

接下来 n 行，每行包含 n 个整数，相邻两个整数之间用一个空格分隔，其中第 i 行第 j 列的值 Li,j​(Li,j​=Lj,i​,Li,i​=0) 表示城市 i 与城市 j 之间直接相连的那条道路的灰尘度的下限值。

输出格式

输出一行包含一个整数表示答案。

输入输出样例

输入 #1复制

3 10
0 2 4
2 0 1
4 1 0
0 2 2
2 0 0
2 0 0

输出 #1复制

2

说明/提示

【样例说明】

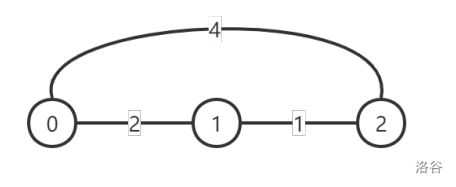
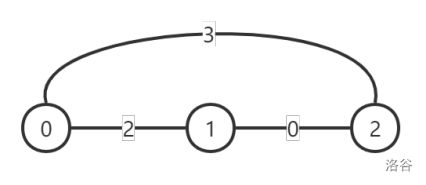
初始时的图如下所示，每条边上的数字表示这条道路的灰尘度：

此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

• d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 3d(0,0)=0,d(0,1)=2,d(0,2)=3；
• d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 1d(1,0)=2,d(1,1)=0,d(1,2)=1；
• d(2, 0) = 3, d(2, 1) = 1, d(2, 2) = 0d(2,0)=3,d(2,1)=1,d(2,2)=0。

初始时的 PP 指标为 (2 + 3 + 1) \times 2 = 12(2+3+1)×2=12，不满足 P \leq Q = 10P≤Q=10;

第一天，00 号城市进行道路改善，改善后的图示如下：

注意到边 (0, 2)(0,2) 的值减小了 11，但 (0, 1)(0,1) 并没有减小，因为 L_{0,1} = 2L0,1​=2 ，所以 (0, 1)(0,1) 的值不可以再减小了。此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

• d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 3d(0,0)=0,d(0,1)=2,d(0,2)=3，
• d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 1d(1,0)=2,d(1,1)=0,d(1,2)=1，
• d(2, 0) = 3, d(2, 1) = 1, d(2, 2) = 0d(2,0)=3,d(2,1)=1,d(2,2)=0。

此时 PP 仍为 1212。

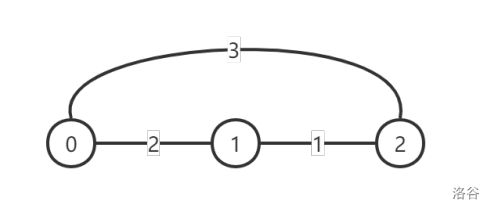
第二天，1 号城市进行道路改善，改善后的图示如下：

此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

• d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 2d(0,0)=0,d(0,1)=2,d(0,2)=2，
• d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 0d(1,0)=2,d(1,1)=0,d(1,2)=0，
• d(2, 0) = 2, d(2, 1) = 0, d(2, 2) = 0d(2,0)=2,d(2,1)=0,d(2,2)=0。

此时的 P 指标为 (2+2)×2=8

所以答案是 2。

【评测用例规模与约定】

• 对于所有评测用例，1≤n≤100，0≤Li,j​≤Di,j​≤105，0≤Q≤2^31−1。

选择灰尘最少的路径其实就是计算最短路问题，对于一个确定的图来说我们可以用floyed来算出所有两点之间的最短路，全部相加即是那个指标P，现在的问题是多少天以后指标P小于Q，注意到随着天数增加P肯定是只减不增的，我们可以二分天数，算出P之后和Q比较一下就知道是长了还是短了，二分结束后输出答案即可

#include 
using namespace std;

int edge[105][105] = {0};
int Min[105][105] = {0};
int n, q;

bool check(int d) {
	int f[105][105];
	//初始化
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			f[i][j] = max(edge[i][j] - 2 * d / n + (bool)(d % n >= i) + (bool)(d % n >= j), Min[i][j]);
		}
	}
	//floyed
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			for (int l = 1; l <= n; l++) {
				f[j][l] = min(f[j][l], f[j][i] + f[i][l]);
			}
		}
	}
	int a = 0;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			a += f[i][j];
		}
	}
	return (a <= q);
}

int main() {
	cin >> n >> q;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> edge[i][j];
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> Min[i][j];
		}
	}
	if (check(0))
		cout << 0;
	else {
		int ans;
		int l = 0, r = 1000000000;
		int mid;
		while (l <= r) {
//			cout << l << ' ' << r << endl;
			mid = (l + r) / 2;
			if (check(mid))
				r = mid - 1;
			else
				l = mid + 1;
		}
		if (l >= 999999999)
			cout << "-1";
		else
			cout << r;
	}
	return 0;
}