matlab矩阵
目录
创建矩阵
1. 直接赋值:
2. 使用内置函数创建:
3. 使用随机数生成矩阵:
特殊矩阵构建函数
1. 对角矩阵(Diagonal Matrix):
2. 上三角矩阵(Upper Triangular Matrix):
3. 下三角矩阵(Lower Triangular Matrix):
4. 反对角矩阵(Anti-Diagonal/Counter-Diagonal Matrix):
5. Toeplitz矩阵(Toeplitz Matrix):
6. 希尔伯特矩阵(Hilbert Matrix):
7. 魔术矩阵(Magic Square):
矩阵的结构和大小的改变
1. 转置(Transpose):
2. 改变大小(Reshape):
3. 压缩和扩展(Flatten and Expand):
4. 拼接(Concatenation):
5. 增加或删除行列:
矩阵旋转
1. 矩阵的旋转:
矩阵下标引用
1. 访问单个元素:
2. 访问多个元素:
3. 访问行或列:
4. 使用逻辑条件作为下标:
5. 修改矩阵元素:
矩阵的大小
1. 获取行数和列数:
2. 获取总元素个数:
3. 判断矩阵的大小:
4. 获取特定维度的大小:
矩阵的合并
1. 水平合并(Horizontal Concatenation):
2. 垂直合并(Vertical Concatenation):
3. 矩阵扩展(Matrix Expansion):
4. 方块合并(Block Concatenation):
Matlab是一种强大的数值计算和科学编程软件,其中的矩阵是非常重要的数据结构。在Matlab中,你可以使用矩阵进行各种数值计算、线性代数运算以及图像处理等操作。
创建矩阵
在Matlab中,可以通过以下方式创建矩阵:
1. 直接赋值:
A = [1 2 3; 4 5 6; 7 8 9];2. 使用内置函数创建:
- zeros函数创建全零矩阵:
B = zeros(3, 4); % 创建一个3行4列的全零矩阵- ones函数创建全1矩阵:
C = ones(2, 3); % 创建一个2行3列的全1矩阵- eye函数创建单位矩阵:
D = eye(4); % 创建一个4行4列的单位矩阵3. 使用随机数生成矩阵:
- rand函数生成在[0,1]区间均匀分布的随机数矩阵:
E = rand(2, 3); % 创建一个2行3列的随机数矩阵- randn函数生成符合标准正态分布的随机数矩阵:
F = randn(3, 3); % 创建一个3行3列的标准正态分布矩阵通过以上方法创建矩阵后,你可以进行各种矩阵运算,如加减乘除、乘法、转置、求逆等。还可以使用索引访问矩阵元素,进行行列操作等。
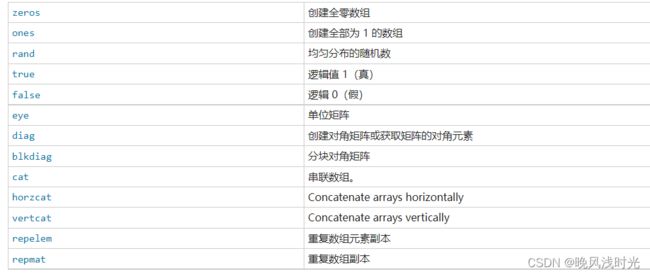
特殊矩阵构建函数
在Matlab中,有一些特殊的矩阵构建函数可以帮助你创建一些常见的特殊矩阵。下面列举一些常用的特殊矩阵构建函数:
1. 对角矩阵(Diagonal Matrix):
- diag函数:创建一个对角矩阵,或者从一个矩阵中提取对角线元素。
A = diag([1 2 3]); % 创建一个3x3的对角矩阵,对角线元素为1, 2, 3
B = diag(A); % 从矩阵A中提取对角线元素2. 上三角矩阵(Upper Triangular Matrix):
- triu函数:创建一个上三角矩阵。
A = triu([1 2 3; 4 5 6; 7 8 9]); % 创建一个上三角矩阵3. 下三角矩阵(Lower Triangular Matrix):
- tril函数:创建一个下三角矩阵。
A = tril([1 2 3; 4 5 6; 7 8 9]); % 创建一个下三角矩阵4. 反对角矩阵(Anti-Diagonal/Counter-Diagonal Matrix):
- fliplr函数:创建一个反对角矩阵。
A = fliplr([1 2 3; 4 5 6; 7 8 9]); % 创建一个反对角矩阵5. Toeplitz矩阵(Toeplitz Matrix):
- toeplitz函数:根据第一行和第一列的元素创建一个Toeplitz矩阵。
A = toeplitz([1 2 3], [1 4 7]); % 创建一个Toeplitz矩阵6. 希尔伯特矩阵(Hilbert Matrix):
- hilb函数:创建一个希尔伯特矩阵。
A = hilb(4); % 创建一个4x4的希尔伯特矩阵7. 魔术矩阵(Magic Square):
- magic函数:创建一个魔术矩阵。
A = magic(3); % 创建一个3x3的魔术矩阵这些都只是一些常见的特殊矩阵构建函数示例,Matlab中还有很多其他用于创建特殊矩阵的函数。你可以查阅Matlab的帮助文档来获得更多详细信息和示例。
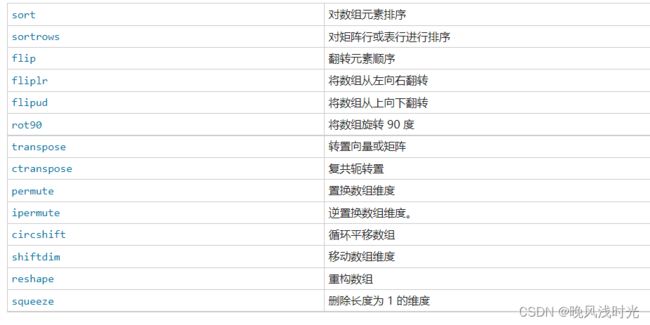
矩阵的结构和大小的改变
在Matlab中,你可以使用各种操作来改变矩阵的结构和大小。下面介绍一些常用的矩阵结构和大小改变操作:
1. 转置(Transpose):
- 使用'转置操作符'(单引号)将矩阵的行和列互换:
A = [1 2 3; 4 5 6];
B = A'; % A的转置矩阵2. 改变大小(Reshape):
- 使用reshape函数将矩阵重新排列为指定的大小:
A = [1 2 3 4; 5 6 7 8];
B = reshape(A, 4, 2); % 将A重新排列为4行2列的矩阵3. 压缩和扩展(Flatten and Expand):
- 使用(:)运算符将矩阵展平成一个列向量(压缩):
A = [1 2; 3 4];
B = A(:); % 将A展平为列向量- 使用reshape函数将列向量重新排列为指定的大小(扩展):
A = [1; 2; 3; 4; 5; 6];
B = reshape(A, 2, 3); % 将A重新排列为2行3列的矩阵4. 拼接(Concatenation):
- 水平拼接:使用[ ]将两个矩阵水平拼接在一起:
A = [1 2; 3 4];
B = [5 6; 7 8];
C = [A B]; % 将A和B水平拼接- 垂直拼接:使用[ ; ]将两个矩阵垂直拼接在一起:
A = [1 2; 3 4];
B = [5 6; 7 8];
C = [A; B]; % 将A和B垂直拼接5. 增加或删除行列:
- 增加行:使用矩阵索引操作符在指定位置插入新行:
A = [1 2; 3 4];
B = [5 6];
C = [A; B]; % 在A的下方插入新行B- 增加列:使用矩阵索引操作符在指定位置插入新列:
A = [1 2; 3 4];
B = [5; 7];
C = [A B]; % 在A的右边插入新列B- 删除行:使用矩阵索引操作符删除指定行:
A = [1 2; 3 4; 5 6];
A(2, :) = []; % 删除第二行- 删除列:使用矩阵索引操作符删除指定列:
A = [1 2 3; 4 5 6];
A(:, 2) = []; % 删除第二列这些是Matlab中常用的矩阵结构和大小改变操作。你可以根据具体的需求选择适合的操作。
矩阵旋转
在Matlab中,你可以使用旋转矩阵来实现对矩阵或向量的旋转操作。下面介绍在2D和3D空间中如何旋转矩阵或向量:
1. 矩阵的旋转:
假设你有一个2D向量或矩阵 `[x; y]`,要对其进行逆时针旋转角度 `theta`:
- 使用旋转矩阵:
theta = pi/4; % 旋转角度 (单位:弧度)
R = [cos(theta) -sin(theta); sin(theta) cos(theta)]; % 旋转矩阵
v = [1; 0]; % 2D向量
rotated_v = R * v; % 旋转后的向量- 也可以使用复数的乘法来实现:
theta = pi/4; % 旋转角度 (单位:弧度)
v = [1; 0]; % 2D向量
rotated_v = exp(1i*theta) * v; % 旋转后的向量矩阵下标引用
在Matlab中,你可以使用下标引用来访问矩阵的特定元素、行或列。下面介绍一些常见的矩阵下标引用方式:
1. 访问单个元素:
- 使用单个下标访问矩阵的元素:
A = [1 2 3; 4 5 6; 7 8 9];
a = A(2, 3); % 访问第2行第3列的元素,结果为62. 访问多个元素:
- 使用范围下标访问矩阵的一部分元素:
A = [1 2 3; 4 5 6; 7 8 9];
B = A(2:3, 1:2); % 访问第2行到第3行,第1列到第2列的元素3. 访问行或列:
- 使用单个下标访问矩阵的一行或一列:
A = [1 2 3; 4 5 6; 7 8 9];
row = A(2, :); % 访问第2行的所有元素
column = A(:, 3); % 访问第3列的所有元素4. 使用逻辑条件作为下标:
- 使用逻辑数组作为下标访问矩阵中满足条件的元素,条件为true的位置对应的元素会被选中:
A = [1 2 3; 4 5 6; 7 8 9];
condition = A > 5; % 找出大于5的元素对应的位置
selected_elements = A(condition); % 访问满足条件的元素5. 修改矩阵元素:
- 使用下标引用给矩阵的特定位置赋新的值:
A = [1 2 3; 4 5 6; 7 8 9];
A(2, 3) = 10; % 将第2行第3列的元素修改为10以上是Matlab中常见的矩阵下标引用方式。你可以根据具体的需求选择适合的方式来操作矩阵的元素、行或列。
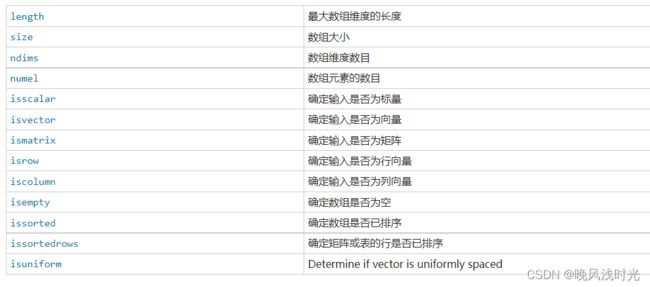
矩阵的大小
在Matlab中,你可以使用size函数来获取矩阵的大小信息。size函数返回一个包含矩阵行数和列数的向量。下面是一些常用的获取矩阵大小的方法:
1. 获取行数和列数:
- 使用size函数获取矩阵的行数和列数:
A = [1 2 3; 4 5 6; 7 8 9];
[m, n] = size(A); % 获取矩阵的行数m和列数n2. 获取总元素个数:
- 使用numel函数获取矩阵的总元素个数:
A = [1 2 3; 4 5 6; 7 8 9];
num_elements = numel(A); % 获取矩阵的总元素个数3. 判断矩阵的大小:
- 使用isequal函数判断矩阵的大小是否与给定的大小一致:
A = [1 2 3; 4 5 6; 7 8 9];
is_same_size = isequal(size(A), [3, 3]); % 判断矩阵的大小是否为3x34. 获取特定维度的大小:
- 如果只关心矩阵的行数或列数,也可以直接使用size函数获取相应维度的大小:
A = [1 2 3; 4 5 6; 7 8 9];
num_rows = size(A, 1); % 获取矩阵的行数
num_columns = size(A, 2); % 获取矩阵的列数以上是Matlab中获取矩阵大小的常用方法。
矩阵的合并
在Matlab中,你可以使用不同的方法将多个矩阵合并为一个更大的矩阵。下面介绍了几种常见的矩阵合并操作:
1. 水平合并(Horizontal Concatenation):
- 使用方括号 [] 将两个矩阵水平合并:
A = [1 2; 3 4];
B = [5 6; 7 8];
C = [A B]; % 水平合并A和B2. 垂直合并(Vertical Concatenation):
- 使用分号 ; 将两个矩阵垂直合并:
A = [1 2; 3 4];
B = [5 6; 7 8];
C = [A; B]; % 垂直合并A和B3. 矩阵扩展(Matrix Expansion):
- 将一个矩阵扩展为更大的矩阵,可以使用水平、垂直合并等操作。例如,将一个矩阵扩展为更大的行数或列数:
A = [1 2; 3 4];
C = repmat(A, 2, 3); % 扩展A为2行3列的矩阵4. 方块合并(Block Concatenation):
- 将多个矩阵按照特定的方块形式合并,可以使用方括号 [] 和分号 ; 来组合矩阵:
A = [1 2; 3 4];
B = [5 6; 7 8];
C = [A B; B A]; % 方块合并A和B需要注意的是,在进行矩阵合并操作时,被合并的矩阵必须具有相同的行数或列数,否则将会导致错误。