代码随想录-刷题第二十六天

216.组合总和III

题目链接：216. 组合总和 III

思路：将问题抽象成树形结构，然后通过回溯法搜索答案。 本题k相当于树的深度，9（因为整个集合就是9个数）就是树的宽度。例如 k = 2，n = 4的话，就是在集合[1,2,3,4,5,6,7,8,9]中求 k（个数） = 2, n（和） = 4的组合。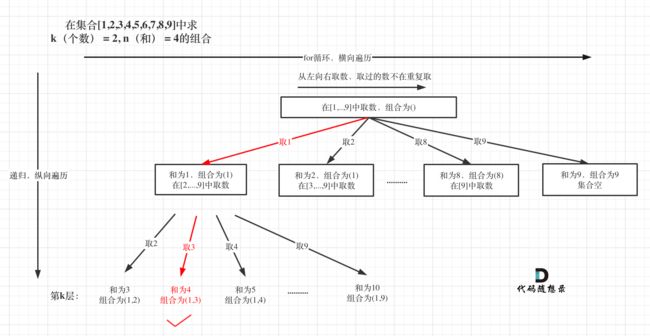

class Solution {
    private List<List<Integer>> res = new ArrayList<>();
    private List<Integer> path = new ArrayList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracking(k, n, 0, 1);
        return res;
    }

    // sum：已经收集的元素的总和，也就是path里元素的总和。
    // start：下一层for循环搜索的起始位置。
    private void backtracking(int k, int n, int sum, int start) {
        if (path.size() == k) {
            if (sum == n) {
                res.add(new ArrayList<>(path));
            }
            // 如果path.size() == k 但 sum != n 直接返回
            return;
        }

        for (int i = start; i <= 9; i++) {
            path.add(i); // 处理
            sum += i; // 处理
            backtracking(k, n, sum, i + 1);
            sum -= i; // 回溯
            path.remove(path.size() - 1); // 回溯
        }
    }
}

做剪枝优化后代码

class Solution {
    private List<List<Integer>> res = new ArrayList<>();
    private List<Integer> path = new ArrayList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracking(k, n, 0, 1);
        return res;
    }

    // sum：已经收集的元素的总和，也就是path里元素的总和。
    // start：下一层for循环搜索的起始位置。
    private void backtracking(int k, int n, int sum, int start) {
        if (sum > n) { // 剪枝操作
            return;
        }

        if (path.size() == k) {
            if (sum == n) {
                res.add(new ArrayList<>(path));
            }
            // 如果path.size() == k 但 sum != n 直接返回
            return;
        }

        for (int i = start; i <= 9 - (k - path.size()) + 1; i++) {
            path.add(i); // 处理
            sum += i; // 处理
            backtracking(k, n, sum, i + 1);
            sum -= i; // 回溯
            path.remove(path.size() - 1); // 回溯
        }
    }
}

---

17.电话号码的字母组合

题目链接：17. 电话号码的字母组合

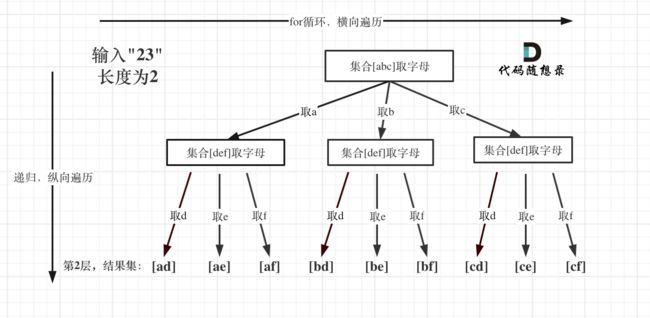
思路：将问题抽象为树形结构，然后用回溯法搜索全部结果。

图中可以看出遍历的深度，就是输入"23"的长度，而叶子节点就是要收集的结果，输出[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”]。

class Solution {
    // 从0到9每个数字对应字母的映射
    private String[] mapping = new String[]{
            "", "", "abc", "def", "ghi",
            "jkl", "mno", "pqrs", "tuv", "wxyz"
    };

    private List<String> res = new ArrayList<>();
    // 每次迭代获取一个字符串，所以会设计大量的字符串拼接，
    // 所以这里选择更为高效的 StringBuild
    private StringBuilder sb = new StringBuilder();

    public List<String> letterCombinations(String digits) {
        if (digits.isEmpty()) {
            return res;
        }
        // 从 digits[0] 开始进行回溯
        backtracking(digits, 0);
        return res;
    }

    // 回溯算法主函数
    private void backtracking(String digits, int start) {
        if (sb.length() == digits.length()) {
            // 到达回溯树底部
            res.add(sb.toString());
            return;
        }
        // 回溯算法框架
        for (int i = start; i < digits.length(); i++) {
            int digit = digits.charAt(i) - '0';
            for (char c : mapping[digit].toCharArray()) {
                // 做选择
                sb.append(c);
                // 递归下一层回溯树
                backtracking(digits, i + 1);
                // 撤销选择
                sb.deleteCharAt(sb.length() - 1);
            }
        }
    }
}

---