西南交通大学【数据结构实验8】
实验内容及要求:
编写控制台应用程序,提供以下菜单项:
- 插入元素
从键盘输入若干两两互不相同的非0整数,直到输入0时停止。将输入的所有非0整数按输入次序插入二叉排序树(初始时是空树)。
插入某个非0整数时,若该整数已在二叉排序树中,则插入该整数失败(应显示提示信息)。
全部整数插入结束后,显示成功插入的整数个数。
- 删除元素
输入一个整数,若它在二叉排序树中,则删除它(提示删除成功与失败)。
- 输出
输出二叉排序树的先序和中序递归遍历结点访问次序。
- 结束程序
实验目的:掌握二叉排序树插入、删除元素的基本算法。
数据结构设计简要描述:
将int型作为此次实验的关键字,通过自定义二叉排序树节点结构存储二叉排序树
// 将int作为元素类型
typedef int elem;
// 自定义二叉排序树节点类型
typedef struct node
{
elem data;
// 左子树 右子树
struct node* lchild, * rchild;
}BSTNode, * BSTree;算法设计简要描述:
创建二叉排序树采用逐个读取value值创建二叉排序树节点,然后逐个插入进二叉树。在插入时先判断此节点的值是否已存在,若存在则插入失败并释放该节点空间。若不存在则通过逐个与树中各节点比较值大小不断向下,得到插入位置,进行节点的插入。
删除节点时先对预删除的节点的值进行查找,若查找失败则删除失败。若查找成功则分为三种情况删除:左右子树均存在、只存在左子树或右子树、叶子结点。后两种情况较为简单不需复杂的变换:叶子结点直接删除,只有一方子树的将子树接到删除节点位置即可。若是左右子树均存在,需找到删除节点左子树中的最大值节点,将此节点接到删除节点的位置,将删除节点的右子树接到此节点的右子树上。
遍历操作采用中序递归遍历和先序递归遍历。
输入/输出设计简要描述:
输入:直接在控制台输入全部整数,两两之间用空格间隔,以0作为结尾代表输入结束。
输出:根据输入操作的不同将不同的结果展示在控制台
编程语言说明:
使用Visual Studio Code编程。 主要代码采用C语言实现 ;动态存储分配采用C++的new和delete操作符实现;输入与输出采用C++的文件流对象和cout流;程序注释采用C/C++规范。
主要函数说明:
// 在二叉排序树中查找
BSTNode* SearchBST(BSTree bt, elem key);
// 在二叉排序树中插入
void Insert(BSTree& bt, BSTNode* p, int& count);
// 创建二叉排序树
void CreBst(BSTree& bt);
// 删除二叉排序树中的节点
void erase(BSTree& bt, elem key);
// 中序递归遍历
void Inorder(BSTree T);
// 先序递归遍历
void Preorder(BSTree T);
// 删除功能
void Delete(BSTree& bt);
// 释放二叉排序树空间
void clear(BSTree& bt);程序测试简要报告:
测试样例(1)
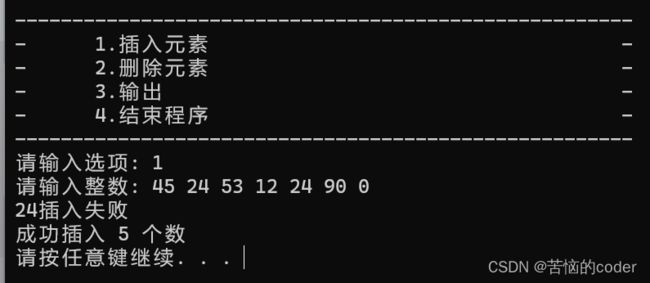
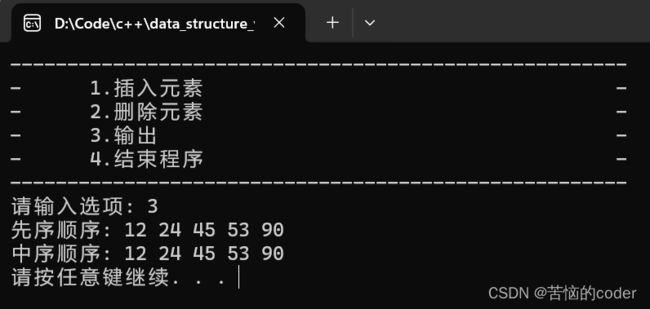
程序输入
二叉排序树示意图
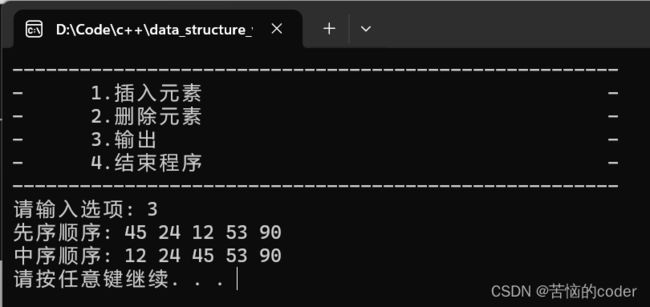
功能测试
结论
程序输出结果与期望输出结果相符。
测试样例(2)
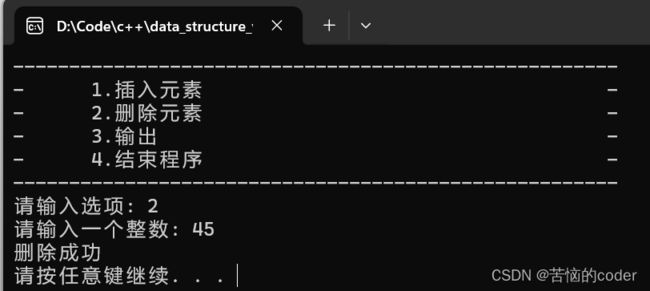
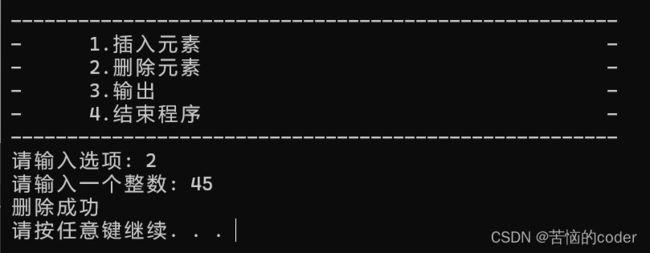
程序输入
二叉排序树示意图
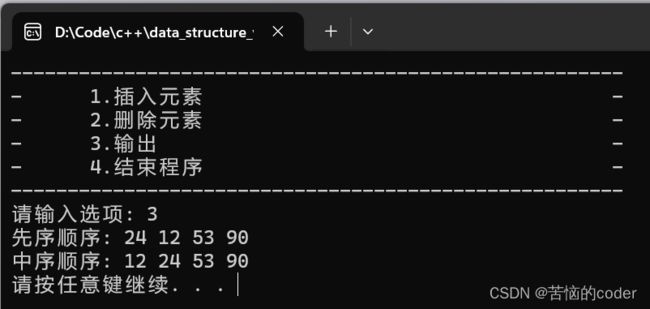
功能测试
结论
程序输出结果与期望输出结果相符。
源程序代码:
#include
using namespace std;
// 将int作为元素类型
typedef int elem;
// 自定义二叉排序树节点类型
typedef struct node
{
elem data;
// 左子树 右子树
struct node* lchild, * rchild;
}BSTNode, * BSTree;
// 在二叉排序树中查找
BSTNode* SearchBST(BSTree bt, elem key) {
// 若bt不为空且bt不是要查找的值
while (bt && bt->data != key)
{
// 如果key比bt小则转到左子树
if (key < bt->data) {
bt = bt->lchild;
}
else {
// 否则转到右子树
bt = bt->rchild;
}
}
// 返回bt 若返回的是NULL则表示未找到
return bt;
}
// 在二叉排序树中插入
void Insert(BSTree& bt, BSTNode* p, int& count) {
// bt为二叉排序树 p为要插入的节点 count记录已插入的个数
// flag为查找p的值是否已在排序二叉树中 若为NULL表示不在可以插入
BSTNode* flag = SearchBST(bt, p->data);
if (!flag) {
// parent为双亲节点
BSTNode* parent = NULL;
// pt为插入的位置节点
BSTNode* pt = bt;
// 通过p的值不断和二叉排序树中的值不断比较找出pt
while (pt)
{
parent = pt;
if (p->data < pt->data) {
pt = pt->lchild;
}
else {
pt = pt->rchild;
}
}
// 如果parent为空表示二叉排序树是空树
if (parent) {
// 比parent小则是左子树
if (p->data < parent->data) {
parent->lchild = p;
}
else {
// 否则是右子树
parent->rchild = p;
}
}
else {
bt = p;
}
// 个数加一
count++;
}
else {
// 如果flag不为空说明p值已在二叉排序树中存在 插入失败
cout << p->data << "插入失败" << endl;
delete p;
}
}
// 创建二叉排序树
void CreBst(BSTree& bt) {
int value;
int count = 0;
cout << "请输入整数: ";
cin >> value;
// 如果value不为0 则插入
while (value != 0)
{
// 创建以value为值的节点
BSTNode* temp = new BSTNode;
temp->data = value;
temp->lchild = NULL;
temp->rchild = NULL;
// 插入
Insert(bt, temp, count);
// 继续读取value
cin >> value;
}
cout << "成功插入 " << count << " 个数" << endl;
}
// 删除二叉排序树中的节点
void erase(BSTree& bt, elem key) {
// f为p的双亲节点
BSTNode* f = NULL;
// p为位置节点
BSTNode* p = bt;
// 通过不断比较查找到p
while (p && key != p->data)
{
f = p;
if (key < p->data) {
p = p->lchild;
}
else {
p = p->rchild;
}
}
// 如果p为空 说明不存在key值节点 删除失败
if (!p) {
cout << "查找失败 删除失败" << endl;
return;
}
// pl为删除节点的左子树
BSTNode* pl = p->lchild;
// pr为删除节点的右子树
BSTNode* pr = p->rchild;
BSTNode* ps;
// 替代p节点位置的节点
BSTNode* s;
// 如果左右子树都存在 查找左子树中最大值
if (pl && pr) {
ps = NULL;
s = pl;
while (s->rchild)
{
ps = s;
s = s->rchild;
}
if (!ps) {
pl = s->lchild;
}
else {
ps->rchild = s->lchild;
}
s->lchild = pl;
s->rchild = pr;
}
else if (pl) {
// 只存在左子树
s = pl;
}
else {
// 只存在右子树
s = pr;
}
// 如果f为空 说明删除根节点
if (!f) {
bt = s;
}
else if (f->lchild == p) {
f->lchild = s;
}
else {
f->rchild = s;
}
delete p;
cout << "删除成功" << endl;
}
// 中序递归遍历
void Inorder(BSTree T) {
/*
此算法采用递归方式实现中序遍历
*/
if (T) {
Inorder(T->lchild);
cout << T->data << " ";
Inorder(T->rchild);
}
}
// 先序递归遍历
void Preorder(BSTree T) {
/*
此算法采用递归方式实现先序遍历
*/
if (T) {
cout << T->data << " ";
Preorder(T->lchild);
Preorder(T->rchild);
}
}
// 删除功能
void Delete(BSTree& bt) {
int value;
cout << "请输入一个整数: ";
cin >> value;
erase(bt, value);
}
// 释放二叉排序树空间
void clear(BSTree& bt) {
if (bt) {
clear(bt->lchild);
clear(bt->rchild);
delete bt;
}
}
int main(void) {
// 选项变量
int choose;
BSTree bt = NULL;
// 标志变量 控制循环
int flag = 1;
while (flag)
{
cout << "------------------------------------------------------" << endl;
cout << "- 1.插入元素 -" << endl;
cout << "- 2.删除元素 -" << endl;
cout << "- 3.输出 -" << endl;
cout << "- 4.结束程序 -" << endl;
cout << "------------------------------------------------------" << endl;
cout << "请输入选项: ";
cin >> choose;
// 防止选项输入导致出错
if (cin.fail()) {
cin.clear();
cin.ignore(10, '\n');
}
switch (choose)
{
case 1:
CreBst(bt);
system("pause");
system("cls");
break;
case 2:
if (!bt) {
cout << "二叉排序树是空树" << endl;
}
else {
Delete(bt);
}
system("pause");
system("cls");
break;
case 3:
cout << "先序顺序: ";
Preorder(bt);
cout << "\n中序顺序: ";
Inorder(bt);
cout << endl;
system("pause");
system("cls");
break;
case 4:
flag = 0;
clear(bt);
break;
default:
cout << "请输入有效选项!!!" << endl;
system("pause");
system("cls");
break;
}
}
return 0;
}