Pearson、Spearman 相关性分析使用
介绍
Pearson 积差相关系数衡量了两个定量变量之间的线性相关程度。 用来衡量两个数据集的线性相关程度,仅当一个变量的变化与另一个变量的比例变化相关时,关系才是线性的。
Spearman等级相关系数则衡量分级定序变量之间的相关程度。斯皮尔曼相关系数不关心两个数据集是否线性相关,而是单调相关。它是基于每个变量的排名值,而不是原始数据,所以斯皮尔曼相关也叫等级相关或者秩相关(即rank)。
简单一句话概括:Pearson 处理变量的数据原始值,而Spearman 处理数据排序值(需要先做变换:transform)
使用比较
如果关系是一个变量减小,而另一个变量增加,但数量不一致,则皮尔逊相关系数为负但大于 −1。在这种情况下,斯皮尔曼系数仍然等于 −1
救救孩子!Spearman、Pearson相关系数傻傻分不清? - A Byte of Biology
# 在100-130的范围随机生成30个点
a <- sample(100:130, 30)
b <- sample(100:130, 30)
df <- data.frame(a, b)
# 画散点图,线性拟合
ggplot(df, aes(x=a, y=b)) + geom_smooth(method="lm") + geom_point() + xlim(0, 140) + ylim(0, 140)
# 计算Pearson和Spearman相关系数
cor.test(a, b, method="pearson")
cor.test(a, b, method="spearman")
##########################################
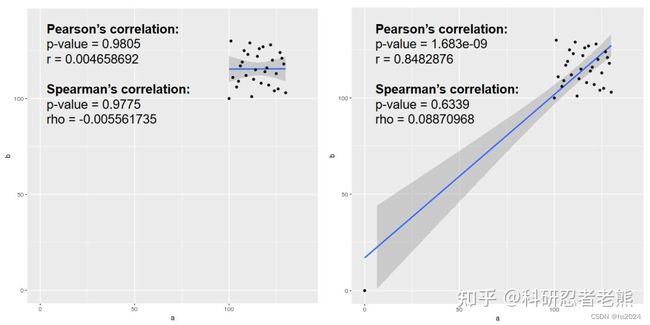
# 再往坐标(0, 0)追加一个点
a <- append(a, 0)
b <- append(b, 0)
df <- data.frame(a, b)
# 再次画散点图,线性拟合
ggplot(df, aes(x=a, y=b)) + geom_smooth(method="lm") + geom_point() + xlim(0, 140) + ylim(0, 140)
# 再次计算Pearson和Spearman相关系数
cor.test(a, b, method="pearson")
cor.test(a, b, method="spearman")Pearson相关系数要求统计资料要是连续型变量,并且符合正态分布,而Spearman相关系数没有这个要求,Pearson相关系数在出现奇异值,或者长尾分布的时候稳定性差,不太靠,而Spearman要相对稳健很多。
下图可以看出,只需要增加一个离群的点,就可以让Pearson相关系数从“不相关”变为“强相关”,所以这个时候Spearman相对更稳。
除了单纯看基因调控的相关性,有些同学是拿到测序数据之后,想分析转录组样本重复相关性。这个时候就有理由假设样本重复线性相关,所以用得比较多的还是Pearson相关系数。但其实转录组测序的表达量不符合正态分布,并且通常都有个很长的“尾巴”(一些极高表达的基因),会导致Pearson相关系数分析的结果可靠性不佳。但也不能因为转录组不符合正态分布就换用Spearman,这样统计效力更差了。可以在做Pearson相关性分析之前先对数据做变换,另外应该加上其他方法进行验证,比如聚类,不要仅仅使用Pearson相关系数。
参考:
1:数学笔记:pearson correlation coefficient VS spearman correlation coefficient_pearson and spearman correlation coefficients-CSDN博客
2:pearson 和spearman的区别~? - 知乎 (zhihu.com)
3:相关性分析和作图-CSDN博客
4:救救孩子!Spearman、Pearson相关系数傻傻分不清? - A Byte of Biology