古典密码学

古典密码及其设计思想

置换密码(换位密码)

不改变实际使用的字母，而是通过重新排列字母顺序来隐藏信息
设S是一个有限集合， ϕ是从S到S的一个映射，如果对任意u,v∈S,当u≠v时， ϕ(u)≠ϕ(v)，则称ϕ为S上的一个置换(Permutation)
设n为某个固定的正整数， “P,C,K” 分别为明文空间、密文空间和密钥空间。 且"P=C" 均是长度为n的字符序列。 “K” 是定义在{1,2,⋯,n}的所有置换的集合。对任何一个密钥σ∈"K" （即一个置换），定义置换加解密如下：
对于一个密钥$\sigma \in "K",p=(p_1,\cdots ,p_n)\in "P",c=(c_1,\cdots ,c_n)\in "C"$ , 定义：
$E_{\sigma }(p)=(c_1,\cdots ,c_n):c_i=x_{\sigma (i)}$
$D_{{\sigma }^{-1}}(c)=(p_1,\cdots ,p_n):p_i=c_{{\sigma }^{-1}(i)}$
这里${\sigma }^{-1}$是σ的逆置换，密钥空间"K" 的大小为n!。

栅栏密码Rail-fence Cipher（W型、Z型）

列置换密码 Columnar Transposition

明文以矩形方式一行行写入，但一列列的读出
密钥是矩形的长度和列读出顺序

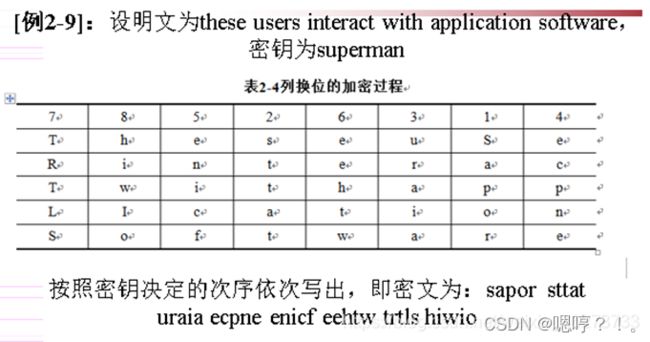
思考：若明文长度为n，列置换密码的密钥空间有多大？n!

周期置换密码——列置换密码的变形

周期变换密码是将明文P按固定长度m分组，然后对每组的字符串按置换σ重新排列位置从而得到密文。
明文为can you understand? 密码：fork（1342字母的前后顺序）。求密文？

即密文为：cyan onuu dser tdan

代换密码（替换密码）

单字母代换

将每个明文字谜独立的映射为密文字母

单表

一个明文字母表对应一个密文字母表

ROT 5/13/18/47密码

ROT 5只对数字进行加密，用当前数字往前数用第5个数字替接当前数字
ROT 13只对字母进行加密，用当前字母往前数用第13个字母替换当前字母
ROT 18将ROT5和ROT13组合一起
ROT 47对数字、字母、常用符号进行编码，按照它们的ASClI值进行位置誉换，用当前字符ASCII值往前数的第47位对应字符替换当前字符，例如当前为小写字母z，编码后变成大写字母K，当前为数字0，编码后变成符号。用于ROT47编码的字符其ASCII值范图是33一126，具体可参考ASCll编码。

Caser密码（加密：后移三位）

移位密码

乘法密码

仿射密码

令$P=C=Z_{26},K=(a,b)\in Z_{26}\times Z_{26}:gcd(a,26)=1,p\in P,c\in C,k\in K$。定义：
$E_k(p)=ap+bmod26$
$D_k(p)=a^{-1}(c-b)mod26$
注意这里要求： gcd(a,26)=1
当b=0时，仿射密码技术退化为乘法密码技术；
当a=1时，仿射密码技术退化为移位替换密码技术
当a=1,b=3时，仿射密码技术退化Caser密码
例：

关于仿射密码的一些思考
思考1：仿射密码的密钥空间大小？
答案：$K=${$(a,b)\in Z_{26}\times Z_{26}:gcd(a,26)=1$}。 b的可能选择有26种， a的可能选择有ϕ(26)=12种。所以仿射密码的密钥空间大小为12×26=312
思考2：证明当gcd(a,26)=1时，仿射密码的解密是唯一的？
证明：假设存在$p_1,p_2\in Z_{26}$, 都是c∈Z_{26}的明文。则有
$a{p}_1+b=a{p}_2+bmod26$
于是$a{p}_1=a{p}_{2}mod26$, 进一步有$26|a(p_1-p_2)$. 又因为gcd(a,26)=1，所以有$26|(p_1-p_2)$。而$p_1,p_2\in Z_{2}6$ ，从而得到$p_1=p_2$.

单表代换密码

明文空间M和密文空间C都是26个英文字母的集合，密钥空间$K=${$\pi :Z_{26}\to Z_{26}|\pi 是置换$}，是所有可能置换的集合。对任意π ∈K，定义:（${\pi }^1$是π的逆置换）
加密变换：eπ(m)=π(m)=c
解密变换：$d\pi （c）$= ${\pi }^1$（c）=m

一般单表代换密码的特点 ：
密钥空间K很大，|K|=26!=4×1026。破译者1微秒试一个密钥，遍历全部密钥需要1013 年。因此，需要引入更先进的密码分析方法
在单表代换下，字母的频率、重复字母的模式和字母组合方式等统计特性（除了字母名称改变以外）均未改变——容易被频度分析破解
密钥π不便记忆

多表

一个明文字母表对应多个密文字母表
为了使密文中不表现出明文的统计特征，一个办法就是使每个明文字母可能被多种密文字母所代换，于是可以通过使用不止一个代换表进行代换来实现。多表代换密码就是多个代换表依次对明文消息的字母进行代换的加密方法。

：代换表的个数，表示代换序列的周期。不同的代换表来轮流代换明文消息中的字母。
如果d=1，多表代换密码退化为单表代换密码，即只有一个代换表。
如果d=∞，则代换序列是非周期无限序列，每个明文都采用不同的代换表进行加密，这其实就是“一次一密”。通常实际应用中采用周期代换密码，也就是使用有限个代换表。

维吉尼亚密码（vigenere）

设m为某个固定的正整数， “P,C,K” 分别为明文空间、密文空间和密钥空间。 且$P=C=Z_{26}^n,K=Z_{26}^m$。对于一个密钥$k=(k_0,k_1,\cdots ,k_{m-1})\in K=Z_{26}^m$, $p=(p_0,\cdots ,p_{n-1})\in P$ , $c=(c_0,\cdots ,c_{n-1})\in C$, 定义：
$E_k(p)=(c_1,\cdots ,c_n):c_i=p_i+k_{i(modm)}mod26$
$D_k(c)=(p_1,\cdots ,p_n):p_i=c_i-k_{i(modm)}mod26$
多个密文表，平滑了频率分布，从而使得密码分析更加困难

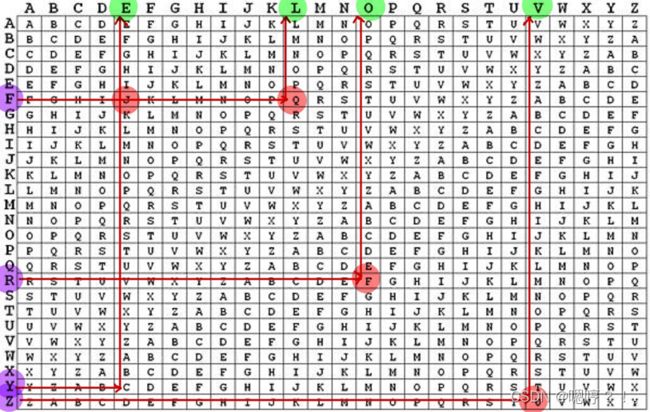
密钥：frzy 密文：qfuc 明文：love
解密：第一个字母，看以f开头的行，对应明码表查找q字母所标示的字母为l。以此类推找出后面字母。所得明文为love。

轮转机

转轮密码机由多个转轮构成，每个转轮旋转的速度都不一样，比如有3个转轮，分别标号为1,2,3，其中1号转轮转动26个字母后，2号转轮就转动一个字母，当2号转轮转动26个字母后，3号转轮就转动1个字母。因此，当转轮密码机转动26X26X26次后，所有转轮恢复到初始状态，即3个转轮密码机的一个周期长度为26X26X26（17576）的多表代换密码。

多字母代换

字母映射以组的方式进行，依赖于其上下文的位置

Playfair Cipher(普莱费尔密码)

基于密钥词的5X5字母矩阵
首先填充密钥词字母，接着将剩余字母填充进矩阵， 然后一次加密两个字母
举例：（加密方法不是死的，可以灵活变通）

1.如果双字母是重复的，插入填充字母X或Z。例如“balloon”被填充为"ba lx lo on"
2.如果双字母位于同一行，用每个字母右边的字母去代替原字母（当行结束后回滚到行首）。例如. “ar” 被加密为 “RM”
3.如果双字母位于同一列，用每个字母下面的字母去代替原字母（当列结束后回滚到列顶部）。例如. “mu” 被加密为"CM"
4.否则，每个字母用与它同一行，与另一字母同一列交叉点的字母代替。例如. “hs” 被加密为“BP”,“ea“被加密为”IM”或"JM"

四方密码 Four Square——Playfair的变形

使加密效果强于其他替换密码，因为频率分析变得更加困难了。

四方密码使用4个预先设置的5×5字母矩阵，每个矩阵包括25个字母，通常字母’j’被融入到’i’中(维基百科上说’q’被忽略，不过这不重要，因为’q’和’j’都是很少出现的字母)，通常左上和右下矩阵式是标准字母排序明文矩阵，右上和左下矩阵是打乱顺序的密钥矩阵。

密钥：example和keyword。
明文：help me 明文分组：he lp me 密文：FY GM KY

希尔密码（Hill Cipher）

基本思想是把m个连续的明文字母代换成m个连续的密文字母
这个代换由密钥决定，这个密钥是一个变换矩阵
解密时只需要对密文做一次逆变换即可

希尔密码的安全性讨论：
与Playfair密码相比，Hill密码的分组长度可以更长（即大于2），由矩阵的维度决定。与Vigenere相比，Hill密码更加安全。
Hill密码中某个明文字母对应的密文字母既与加密矩阵相关，也与该分组其他字母相关，而Vigenere中，明文字母只与加密密钥相关。

古典密码体制的攻击方法

穷举攻击

敌手具有的能力：唯密文(Ciphertext-only attack)攻击
攻击成功的要求：
加解密算法已知
密钥空间小
明文易于识别

频度分析

单表代换密码频度分析：西文语言—出版物中字母及组合的出现频度有统计规律，元音字母频度高。（单字母频率、双字母频率、三字母频率等等）

密文分析时，可先统计密文中各个字母出现的频率，然后猜测出现次数最多的字母为e的密文，次多的字母为t，或者a，或者o。然后用这两个字母来替换密文，根据搭配关系、词首尾关系继续分析、猜测剩余的密文，最终得到全部的明文

综合工程