技术干货 | MindSpore AI科学计算系列（三）：SciML分析

本篇是MindSpore AI科学计算系列(一）的续篇。我们将在前述介绍PINNs和英伟达SimNet工具包的基础上，重点分析AI科学计算领域的另外一个软件包SciML。

点击↓回顾链接跳转查看文章

技术干货 | MindSpore AI科学计算（一）：PINNS和Simnet分析

SciML软件包

SciML是由NumFOCUS组织赞助的AI科学计算开源软件包。该组织旨在开发和维护的一套功能丰富和高性能的科学机器学习工具集，拥有非常活跃的社区并且聚集了大批优秀的开发者。与SimNet不同的是，SciML主要是基于Julia语言开发。该语言源于高性能数值分析和科学计算的需要而设计。正因如此，SciML具有非常优秀的并行和分布式计算能力，可以便捷的利用社区众多成熟的高性能基础代码。

图一 SciML的研究主题：领域感知、可解释性和鲁棒性

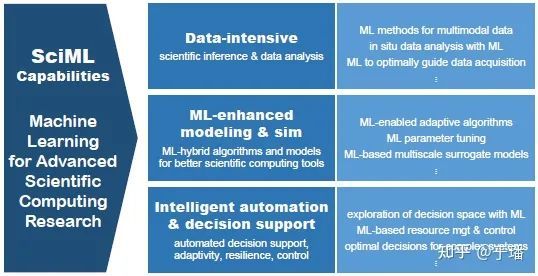
图二 SciML的应用主题：科学推理和数据挖掘、机器学习增强建模、智能自动化和决策支持

SciML的远景目标就是生成一个统一科学计算与机器学习的工具包，它包含科学计算与机器学习相融合领域的全部内容(见图一、二)。该工具包在集成传统科学计算方法的基础上，进一步融合AI领域的最前沿算法，提供高度模块化、高扩展性、高性能的生态系统，以此促进科学计算领域的基础性和应用型问题的研究。除了微分方程求解器等科学计算模块，该软件包还提供了一套针对正向求解、反问题、自动模型发现和决策推理等问题的方法论。

SciML主要模块

与SimNet/DeepXDE不同，SciML软件包并不以TensorFlow或者Pytorch等较为成熟的AI训练框架为后端。它是充分利用 Julia语言在科学计算领域的优势，发展出的一整套科学计算与机器学习相融合的生态系统。该工具包含数量庞大的应用库，下面仅列出其中部分的核心组件。

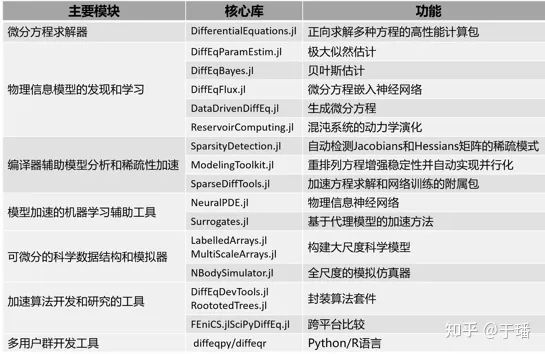
图三 SciML的主要模块和功能介绍

SciML优势

SciML软件包是科学机器学习和微分方程建模工具的开发套件的集合，它提供了丰富的工具库并由此组成了一个连贯的生态系统。相比于其他工具包，SciML具有如下四个方面的优势：

1、多功能、多平台支持

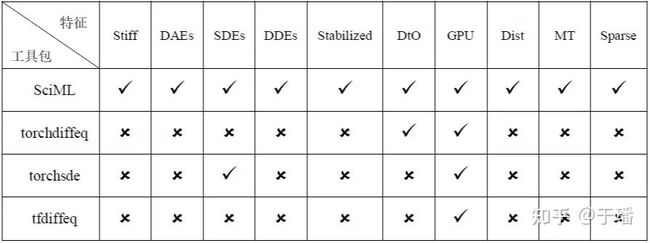
从下表中的对比中可以看出，SciML生态系统是唯一一个同时支持刚性常微分方程（Stiff ODEs）、微分代数方程（DAEs）、随机微分方程（SDEs）、延迟微分方程（DDEs）、稳定邻域、分布式和多线程计算，并且与深度学习集成的微分方程求解器库 。这些模板化的求解器支持任意维度的数组和数据类型、多种浮点数精度的数值运算，并支持基于GPU/MPI/多线程等的计算形式和其他功能。

表一 不同工具包特性支持情况对比

2、高性能

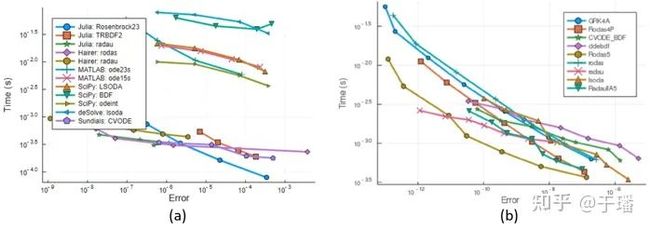
SciML是基于Julia语言开发，在科学计算领域具有高性能的天然优势(如下图四所示，不同工具包性能对比)。此外，性能也是SciML所优先考虑的问题，在社区内所有关于性能的议题都将会被作为bug被处理，从而支持科学机器学习的高性能扩展。最后，SciML紧跟计算硬件发展的脚步，确保与最新的高性能计算工具相兼容。SciML会随着新硬件技术的发布不断更新编译器后端从而维护一个能在所有主要平台上工作的工具链。

图四 不同工具求解刚性Hires方程的性能对比

相比于SUNDIALS CVODE(C++)以及Fortran方法（Radau）, SciML的微分方程求解器库具有明显的性能优势。

在算法层面，SciML同样致力于性能提升。科学模型通常包含局部性的结构，尤其是在离散方程中通常只有邻近网格点间物理量的耦合。这种局部性导致了程序结构中张量表达的稀疏性。SciML基于这个特征建立了一套相互关联的工具，可以直接在被模拟的模型上生成数值求解器代码，从而实现明显的性能提升。

3、高可靠性和鲁棒性

当前，SciML所有的软件包都经过了科学模拟和机器学习工具的常规和鲁棒性的测试。在基准测试方面，SciML设置自动更新以获得更好的性能回归跟踪，并不断增加包括MPI和GPU在内的新基准SciML Benchmarks（https://github.com/SciML/SciMLBenchmarks.jl）。

支持DifferentialEquations.jl微分方程求解器和Flux.jl深度学习库之间相连接的DiffEqFlux.jl工具仍在持续开发中。将代理模型Surrogates.jl与DifferentialEquations.jl和Zygote.jl等机器学习辅助工具进行常规测试，这确保代理模型工具可以在多种形式的微分方程上进行训练，然后在深度学习堆栈里面使用。正是这种互联性将使下一代SciML方法论得到生产化，从而影响 “大科学”和工业应用。

4、加速算法开发和研究的丰富工具库

SciML致力于促进数值模拟方法和科学机器学习等领域的尖端研究。基于此目标开发的许多工具都能自动完成基准测试和新方法的验证过程，从而确保它们的安全性和可靠性，并加速这些方法向出版物和用户的转化过程。SciML通过DiffEqDevTools.jl和RoototedTrees.jl模块使能更多的研究社区利用和发展其所提供的大型封装算法套件来快速测试和部署新算法。其对外部工具的包装器，如模块FEniCS.jl和SciPyDiffEq.jl，可以轻松地进行跨平台比较。另外，SciML也同时提供科学机器学习中最新算法的高级实现，比如利用神经网络从符号描述中自动求解微分方程，并生成无网格的离散器。

案例介绍

SciML在正向求解微分方程、反问题、参数估计、决策推理以及训练通用和神经常微分方程等领域被广泛使用，并建立起众多科学机器学习软件生态系统的基准案例。本节仅抽取两个简单案例介绍SciML工具集的使用方法。

1、神经常微分方程

本小节以Lotka-Volterra方程为例介绍如何利用SciML正向求解该方程以及如何将其嵌入神经网络。Lotka-Volterra方程是用于描述生物系统中掠食者与猎物种群规模消长的经典动态模型。作为一个二元一阶非线性微分方程组，该方程具有如下形式：

SciML的DifferentialEquations.jl模块提供了微分方程求解的工具，并且提供了多功能的选项，如自定义精度、残差以及求解器算法等。在给定初始条件后，参考如下代码调用solve的计算接口即可以直接给出如下图五(a)所示的解。

using DifferentialEquations, Plots
## Setup ODE
function lotka_volterra(du, u, p, t)
x, y = u
alpha, beta, delta, gama = p
du[1] = dx = alpha * x – beta * x * y
du[2] = dy = -delta * y + gama * x * y
end
u0 = [1.0, 1.0]
tspan = (0.0, 10.0)
p = [1.5, 1.0, 3.0, 1.0]
prob = ODEProblem(lotka_volterra, u0, tspan, p)
## Verify ODE solution
Sol = solve(prob, Tsit5())
plot(Sol)

图五 （a）SciML正向求解Lotka-Volterra方程的计算结果; (b) 神经常微分方程网络输出结果

相比于残差网络等经典结构，神经微分方程是以连续的方式对数据建模，从而连续化神经网络层级。下面我们将上述常微分方程嵌入神经网络的框架中，然后继续使用标准的优化技术，比如ADAM来优化它们的权重。具体实现如下代码所示，微分方程层diffeq_rd接收积分的参数p，把它放在由上述prob所定义的微分方程中，然后用选择的参数（求解器、残差等）进行求解。为确定使得损失函数最小化的参数p，Flux训练这样一个网络：即神经网络的前向恰好包含解一个常微分方程。由于损失函数会在猎物数量远离1时就增加惩罚，所以训练结果找到的掠食者与猎物族数量都是趋近于常数1(如图五(b)所示)。在这个案例中仅包含一层求解ODEs的网络结构，事实上可以在神经网络的任何位置添加它。

## Build a neural network that sets the cost as the difference from the generated data and 1
p = [2.2, 1.0, 2.0, 0.4]
p=Flux.Params([p]) # Initial parameter vector
function predict_rd() # 1-layer neural network
diffeq_rd(p, prob, Tsit5(), saveat=0.1)[1, :]
end
loss_rd() = sum(abs2, x-1 for x in predict_td()) # loss function
## Optimize the parameter so the ODE’s solution stays near 1
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
Flux.train!(loss_rd, [p], data, opt)
plot(solve(remake(prob,p=Flux.data(p)),Tsit5(),saveat=0.1),ylim=(0,6))

2、PINNs求解泊松方程

本节简要介绍基于PINNs求解泊松方程的实现方法。我们考虑如下形式的方程：

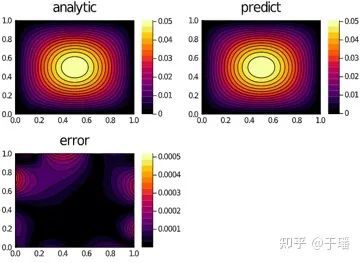
在PINNs中，神经网络利用物理方程的符号描述自动求解PDE。解函数通过神经网络来逼近，损失函数则由物理方程和初边值条件进行约束。如下示例代码所示，解函数逼近器chain由三层Dense网络结构串联而成，该结构联合求解域的采样点构成PhysicsInformNN网络。微分方程和边界条件作为PDESystem接口的入参用于量化损失函数，训练网络即可得到该方程的近似解。基于该网络训练的权重可以将微分方程的解泛化至整个场区域，与解析解的对比结果如图六所示，可以发现二者的误差很小，这表明通过神经网络得到的近似解可以准确的逼近解析解。

using NeuralPDE, Flux, ModelingToolkit, GalacticOptim, Optim, DiffEqFlux                     
@parameters x, y
@variables u(..)
Dxx = Differential(x)^2
Dyy = Differential(y)^2
## 2D PDE
Eq = Dxx(u(x, y) + Dyy(u(x, y)) ~ -sin(pi * x) * sin(pi * y)
## Boundary conditions
bcs = [u(0, y) ~ 0.f0, u(1, y) ~ -sin(pi*1) * sin(pi*y), u(x, 0) ~ 0.f0, u(x, 1) ~ -sin(pi*x) * sin(pi*1)]
## Space and time domains
domains = [x ∈ IntervalDomain(0.0, 1.0), y ∈ IntervalDomain(0.0, 1.0)]
## Discretization
dx = 0.1
## Neural network
dim = 2
chain = FastChain(FastDense(dim, 16, Flux.σ), FastDense(16, 16, Flux.σ), FastDense(16, 1))
discret = PhysicsInformedNN(chain, GridTraining(dx)) # PINNs model
pde_system = PDESystem(eq, bcs, domains, [x, y], [u])
prob = discretize(pde_system, discret)
res = GalacticOptim.solve(prob, Optim.BFGS(); maxiters=1000)
phi = discret.phi

图六 PINNs求解泊松方程的对比结果

总结与展望

数学建模和量化求解是科学计算的主要任务，诸如天体运动、海洋、气象以及材料、生物医药等领域的典型问题通常可以通过微分方程来进行建模，然后利用科学计算方法来求解以获得量化指标。科技发展到今天，一方面，科学探究的时空尺度已经进入到极大(天文单位)或者极小(微纳米甚至量子单位)尺度的深水区，观察数据不足的窘境导致归纳建模难以取得令人信服的结果，多学科领域的交叉同样使得物理建模面临理论困境。另一方面，已有模型通常伴随着不同时空尺度以及物理量间的非线性耦合，该类问题的求解一直是科学计算领域极具挑战性的课题。

近年以来，人工智能技术的突飞猛进在深刻影响机器视觉和自然语言处理等领域的同时，也为科学计算提供了一种新的范式。AI方法可以基于实验或者计算产生的数据对所求解的问题直接进行可计算建模；也可以通过直接耦合控制方程和定解条件，无需监督数据即可得到复杂问题的有效解答。将数据与物理定律相结合在正向求解、反问题以及数据同化等领域也同样展现出了非凡的能力。目前以SimNet和SciML为代表的仿真工具包，深度集成了科学计算和AI领域的前沿技术，已经逐步使能在科学探究和工程应用的诸多领域。

与此同时，基于物理定律和推理演绎来进行建模的科学计算模式也对面向数据的AI技术提出了更高的需求和启发，比如高阶自动微分技术、可解释性等。因此，AI与科学计算的结合，势必会相互推动两个领域的共同发展。

目前MindSpore团队分别从物理驱动和数据驱动的AI方法出发，致力于在科学计算领域发展新的算法并开发高性能和易用的AI仿真框架，后续有机会再跟大家分享。同时，我们也欢迎广大的AI科学计算爱好者和研究者加入我们，共同探索AI科学计算这一新课题。

参考文献

1. Scientific Machine Learning (SciML) Projects(https://julialang.org/jsoc/gsoc/sciml/).

2. SciML: Open Source Software for Scientific Machine Learning(https://sciml.ai/).

3. DiffEqFlux.jl — A Julia Library for Neural Differential Equations. Accessed at: DiffEqFlux.jl - A Julia Library for Neural Differential Equations(https://arxiv.org/abs/1902.02376).

4. Universal Differential Equations for Scientific Machine Learning. Accessed at: Universal Differential Equations for Scientific Machine Learning(https://arxiv.org/abs/2001.04385).

5. Workshop Report on Basic Research Needs for Scientific Machine Learning: Core Technologies for Artificial Intelligence. Accessed at: Workshop Report on Basic Research Needs for Scientific Machine Learning: Core Technologies for Artificial Intelligence (Technical Report)(https://www.osti.gov/biblio/1478744-workshop-report-basic-research-needs-scientific-machine-learning-core-technologies-artificial-intelligence).