数字信号处理翻转课堂笔记10——快速傅立叶变换算法（FFT）&1～4章综合题目
数字信号处理翻转课堂笔记10
Flipped Classroom10 of DSP
教材：《数字信号处理（第五版）》西安电子科技大学出版社，高西全、丁玉美著
一、要点
1、频域抽取法基2FFT（DIF-FFT）的原理及其蝶形运算分解图（重点）；
2、IDFT的高效算法；
3、其他进一步减小计算量的措施：多类蝶形单元运算、旋转因子的生成、实序列的FFT算法（一般了解）；
4、一~四章有关信号频域分析内容的回顾。
二、问题与解答
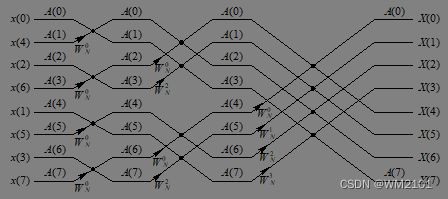
1、画出16点序列的DIF-FFT蝶形运算分解图， 介绍DIF-FFT算法的思路和基本原理。对DIF-FFT和DIT-FFT在原理、蝶形运算结构、输入输出排序等方面进行比较。
2、IDFT的高效算法与DFT的高效算法有何联系与区别？画出8点DIF-IFFT的蝶形运算结构图。
3、教材习题1：如果某通用单片计算机的速度为平均每次复数乘需要4us，每次复数加需要1us，用来计算N=1024点的DFT，问直接计算需要多少时间。用FFT计算呢？照这样计算，用FFT进行快速卷积来对信号进行处理时，估计可实现实时处理的信号最高频率。
4、简要叙述进一步减少计算量的主要措施及其基本思路。多类蝶形运算在减少计算量的同时，在程序设计中会带来什么别的问题？
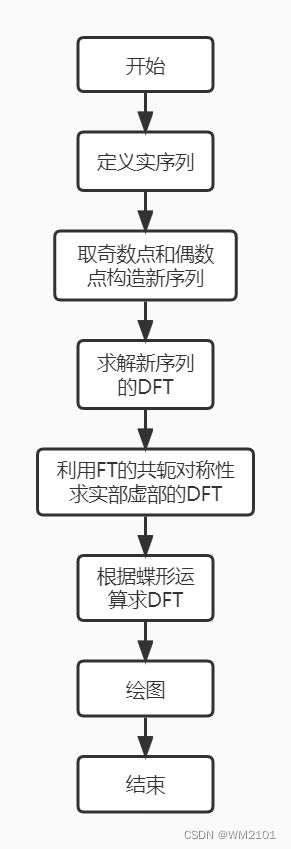
5、任取1个4096点实序列，用MATLAB编程，采用一次2048点的FFT来计算该实序列的DFT。要求给出实现原理分析和程序流程图。
6、
1、DIF-FFT和DIT-FFT的比较
画出16点序列的DIF-FFT蝶形运算分解图， 介绍DIF-FFT算法的思路和基本原理。对DIF-FFT和DIT-FFT在原理、蝶形运算结构、输入输出排序等方面进行比较。
（1）DIF-FFT算法的思路和基本原理：
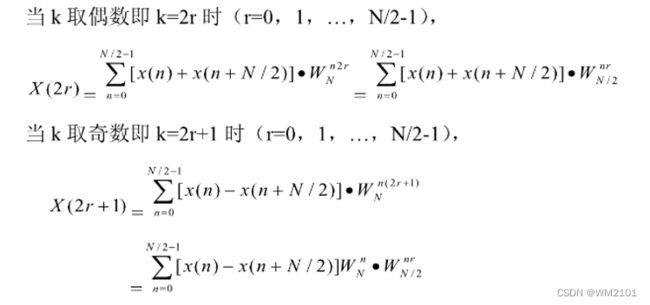
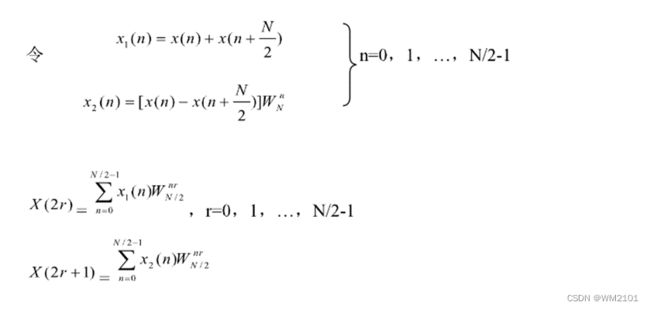
即把一个N点DFT变换为求两个N/2点DFT的运算。以此类推，进一步分解为两个N/4点DFT，进行二次和二次以上的分解。
（2）DIF-FFT和DIT-FFT在原理、蝶形运算结构、输入输出排序的比较：
原理：DIF-FFT是频率抽取法，DIT-FFT是时域抽取法；
蝶形运算结构：DIT-FFT先进行DFT，再蝶形运算，序列先乘旋转因子后相加减
DIF-FFT先蝶形运算，再进行DFT，序列先相加减后乘旋转因子。
输入输出排序：DIF-FFT输出倒序，输入顺序；DIT-FFT输入倒序，输出顺序。
频率抽取法与时间抽取法的基本蝶形是互为转置的。
2、IDFT的高效算法与DFT的高效算法的关系
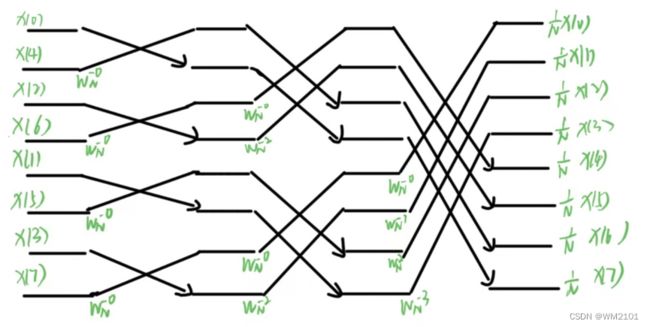
IDFT的高效算法与DFT的高效算法有何联系与区别？画出8点DIF-IFFT的蝶形运算结构图。
8点DIF-IFFT的蝶形运算结构图：
8点DIT-FFT
8点DIT-IFFT
8点DIF-FFT
8点DIF-IFFT
3、DFT与FFT计算速度的直观比较
教材习题1：如果某通用单片计算机的速度为平均每次复数乘需要4us，每次复数加需要1us，用来计算N=1024点的DFT，问直接计算需要多少时间。用FFT计算呢？照这样计算，用FFT进行快速卷积来对信号进行处理时，估计可实现实时处理的信号最高频率。
4、进一步减少计算量的措施及其“副作用”
简要叙述进一步减少计算量的主要措施及其基本思路。多类蝶形运算在减少计算量的同时，在程序设计中会带来什么别的问题？
主要措施：
1、多类蝶形单元运算
2、预先生成旋转因子
3、用N/2点FFT计算N点实序列的FFT
问题：
1、增加代码量
2、因为计算机是流水线结构，所以多类蝶形运算的“跳转”会降低电脑工作效率
5、FFT的matlab实现
任取1个4096点实序列，用MATLAB编程，采用一次2048点的FFT来计算该实序列的DFT。要求给出实现原理分析和程序流程图。
原理分析：
代码：
%% 代码：
clc,clear
n = 1:4096;
x = cos(2*pi*0.15*n) + cos(2*pi*0.3*n);
N = length(x)/2;
% x1为偶数项,x2为奇数项
for n = 1:N
x1(n) = x(2*n-1);
x2(n) = x(2*n);
end
% 组成新序列，并一次求解x1,x2的DFT,X1,X2
xx = x1+1j*x2;
XX = fft(xx,N);
X1(1)=real(XX(1));
X2(1)=imag(XX(1));
for n=2:N
X1(n) = 0.5 * ( XX(n) + conj(XX(N+2-n)));
X2(n) = -1j * 0.5 * ( XX(n) - conj(XX(N+2-n)));
end
% 用1次蝶形计算X前N项和后N项
for n = 0:N-1
X(n+1) = X1(n+1) + exp(-1j*pi*n/N) * X2(n+1);
X(n+1+N) = X1(n+1) - exp(-1j*pi*n/N) * X2(n+1);
end
% 图形展示
subplot(2,1,1)
stem(abs(fft(x)))
title('直接计算','fontname','宋体','fontsize',15);
subplot(2,1,2)
stem(abs(X))
title('用一次2048点的FFT','fontname','宋体','fontsize',15);
运行结果：
分析：用一次2048点的DFT，会减少运算量，但也会增加程序的复杂度。
编程思路：
6、一到四章综合题目
代码：
clear;
syms t
xt=exp(-1000*abs(t));
Xw=fourier(xt);
N=512;
Fs=1000;
n=-N/2/Fs:1/Fs:(N-1)/2/Fs;
xn=exp(-1000*abs(n));
Xk=fft(xn,N); %Xk是序列平移N/2之后的频谱的离散化
k=0:N-1;
X=(-1).^k.*Xk; %去除序列平移对DFT的影响
Y=fftshift(X);
figure(1)
subplot(4,1,1)
stem(0:N-1,real(Xk));
title('DFT结果(1kHz采样)');
xlim([0 511])
xlabel('k')
subplot(4,1,2)
plot(pi*(-1:2/N:(N-1)/N),real(Y));
xlim([-pi pi])
ylim([0 2.2]);
title('DFT结果转换为序列的频谱(1kHz采样)')
xlabel('数字角频率(rad)')
subplot(4,1,3)
w=2*pi*(-N/2:N/2-1)*Fs/N;
plot(w,real(Y)/Fs);
xlim([-2*pi*Fs/2 2*pi*Fs/2])
ylim([0,0.0022]);
title('DFT分析得到的模拟信号频谱(1kHz采样)')
xlabel('模拟角频率（rad/s）')
subplot(4,1,4)
fplot(abs(Xw),[-2*pi*Fs/2 2*pi*Fs/2])
ylim([0,0.0022])
title('模拟信号理论频谱([-Fs/2,Fs/2]区间)')
xlabel('模拟角频率（rad/s）')
Fs=5000;
n=-N/2/Fs:1/Fs:(N-1)/2/Fs;
xn=exp(-1000*abs(n));
xn1=[xn(257:512) xn(1:256)]; %转换为周期延拓后的主值序列
Xk=fft(xn1,N);
k=0:N-1;
X=Xk;
Y=fftshift(X);
figure(2)
subplot(4,1,1)
stem(0:N-1,real(Xk));
title('DFT结果(5kHz采样)');
xlim([0 511])
xlabel('k')
subplot(4,1,2)
plot(pi*(-1:2/N:(N-1)/N),real(Y));
xlim([-pi pi])
ylim([0 11]);
title('DFT结果转换为序列的频谱(5kHz采样)')
xlabel('数字角频率(rad)')
subplot(4,1,3)
w=2*pi*(-N/2:N/2-1)*Fs/N;
plot(w,real(Y)/Fs);
xlim([-2*pi*Fs/2 2*pi*Fs/2])
ylim([0,0.0022]);
title('DFT分析得到的模拟信号频谱(5kHz采样)')
xlabel('模拟角频率（rad/s）')
subplot(4,1,4)
fplot(abs(Xw),[-2*pi*Fs/2 2*pi*Fs/2])
ylim([0,0.0022])
title('模拟信号理论频谱([-Fs/2,Fs/2]区间)')
xlabel('模拟角频率（rad/s）')
（1）如下图，左边取256个点，右边取255个点，这是由n=0和t=0对应不上而决定的。或者也可以将右边的进行周期延拓形成图中下方的结果。通过乘以-1的k次方来消除时域平移的影响。
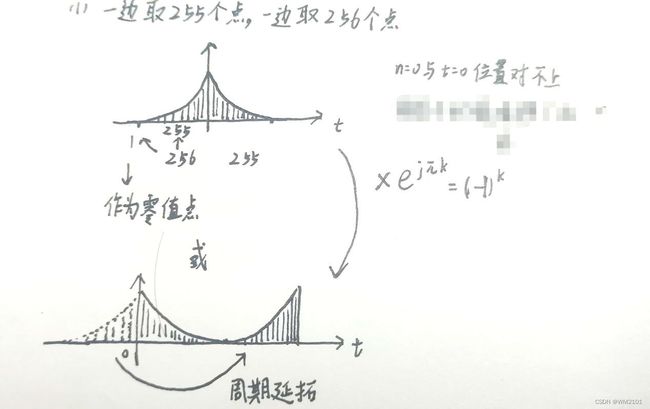
（2）利用fftshift函数将零频率分量移到频谱中心。
（3）-π对应- Fs/2,π对应Fs/2。
（4）频谱的“高矮胖瘦”不同，1kHz的幅值要高于5kHz的幅值。因为1kHz在高频的幅值幅度要比5kHz高，经过延拓之后，会产生频谱混叠，所以混叠后1kHz的幅值要高于5kHz的幅值。
三、反思总结
1、matlab编程：
conj为求复共轭的函数
2、在第二题的DIF-IFFT图中，箭头位置应改为与DIT-FFT相同的位置。