初级数据结构(三)——栈
| 文中代码源文件已上传:数据结构源码 <-上一篇 初级数据结构(二)——链表 | 初级数据结构(四)——队列 下一篇-> |
1、栈的特性
1.1、函数栈帧简述
即使是刚入门几天的小白,对栈这个字也应该略有耳闻。在操作系统层面,栈是系统在内存中划分的一整块连续的地址范围。并且系统对于单个程序在栈区的空间使用也是连续的。以一段代码举例:
void FunctionInside()
{
/* ... */
}
void Function_1()
{
/* ... */
}
void Function_2()
{
/* ... */
FunctionInside();
/* ... */
}
int main()
{
Function_1();
Function_2();
return 0;
}在运行上述代码时,首先调用 main 函数,系统将为 main 函数在栈上单独开辟一块空间供 main 函数使用,这块空间称作 main 函数的栈帧。而当在 main 中调用 Function_1 时,系统又在 main 函数栈帧之上为 Function_1 开辟一块 Function_1 的栈帧。而随着 Function_1 函数调用结束, Function_1 的栈帧也被销毁,该栈帧的空间归还给操作系统。
而进入 Function_2 函数时,系统同样为 Function_2 开辟一块栈帧。如果如上述代码中的 Function_1 和 Function_2 是连续调用的话, Function_2 栈帧很可能覆盖之前 Function_1 被销毁的栈帧空间。此时进入 Function_2 函数内部,又在内部调用 FunctionInside 函数。此时,系统将在 Function_2 栈帧之上为 FunctionInside 创建栈帧。
随着 FunctionInside 调用结束 FunctionInside 栈帧也随之归还,今儿回到 Function_2 的栈帧空间。当然, Function_2 调用结束后, Function_2 的栈帧也将归还,并回到 main 函数的栈帧空间。最后随着程序结束,main 函数的栈帧也随之销毁。
或许有点绕。但看上图也不难发现其规律,这就是栈的特性:后入先出、先入后出,也称为 LIFO ( Last In First Out )。
1.2、栈结构
基于某些需求(如通过程序判断记录数学公式字符串的大中小括号是否配对、计算字符串中的数学公式的值、甚至最基本的数组倒序等),程序的数据处理需要用到后入先出的特性,对这类数据进行操作的结构就称为栈结构。
栈结构的实现仍然是通过顺序表或者链表实现,只是在存取数据时必须遵循 LIFO 的规则。并且,栈结构不存在改和查的操作。如果要,必须将尾部数据至需要修改的数据之间的元素依次弹出后重新依次写入新数据,至于查,只允许查看尾部元素,一旦查看必须弹出。
通常栈结构都用顺序表创建较为方便,因此以下便以顺序表的方式进行演示。同时最后附上链表实现栈结构的代码。
2、栈创建
2.1、文件结构
与之前章节相同,依然创建三个文件,文件名如下:
stack.h :用于创建项目的结构体类型以及声明函数;
stack.c :用于创建栈各种操作功能的函数;
main.c :仅创建 main 函数,用作测试。
2.2、前期工作
stack.h 中内容如下:
#include
#include
#include
#include
//存储数据类型的定义及打印占位符预定义
#define DATAPRT "%d"
typedef int DATATYPE;
//栈主体
typedef struct Stack
{
DATATYPE* data; //数据段
size_t top; //栈顶位置下标
size_t capacity; //开辟空间记录
}Stack;
//函数声明---------------------------------
//初始化
extern int StackInit(Stack*);
//销毁
extern void StackDestroy(Stack*);
//入栈
extern void StackPush(Stack*, DATATYPE);
//出栈
extern void StackPop(Stack*); 然后 stack.c 中先创建初始化及销毁的两个函数。这里需要注意的是对结构体中的 top 值的操作。虽然这个值等同于顺序表中的 size ,但需要区分 top 是储存栈结构最后一个数据的下标。顺序表中的空表 size 则是等于 0 ,取顺序表的最后一个元素下标都是以 size - 1 进行操作,而对于栈来说,如果是空栈,top 则置为 -1 :
#include "stack.h"
//初始化
int StackInit(Stack* st)
{
//参数判断
if (!st)
{
fprintf(stderr, "Illegal Stack Address\n");
return;
}
//初始开辟1个数据位
st->data = (DATATYPE*)malloc(sizeof(DATATYPE) * 1);
if (!st->data)
{
fprintf(stderr, "Malloc Fail\n");
return -2;
}
st->top = -1;
st->capacity = 1;
return 0;
}
//销毁
void StackDestroy(Stack* st)
{
//参数判断
if (!st)
{
fprintf(stderr, "Illegal Stack Address\n");
return;
}
//释放
free(st->data);
st->data = NULL;
st->top = -1;
st->capacity = 0;
}在 main.c 中则预先创建一个结构体变量,无需进行其他操作。
#include "stack.h"
int main()
{
Stack st;
return 0;
}3、栈的数据操作
3.1、入栈
入栈实际上就是顺序表的尾插,具体实现过程可以参考第一篇顺序表中的插入数据操作。这个功能实现起来并不复杂。此外跟顺序表一样,如果已开辟的空间不足则需要进行扩容操作。这里可以将扩容封装为一个函数,使代码看起来更简洁。此外,由于扩容函数仅在该代码文件内调用,可以加上 static 修饰。
在 static.c 中加入以下代码:
//扩容
static void StackExpand(Stack* st)
{
//参数判断
if (!st)
{
fprintf(stderr, "Illegal Stack Address\n");
return;
}
DATATYPE* temp = (DATATYPE*)realloc(st->data, sizeof(DATATYPE) * st->capacity * 2);
if (!temp)
{
fprintf(stderr, "Realloc Fail\n");
return;
}
st->data = temp;
st->capacity *= 2;
}
//入栈
void StackPush(Stack* st, DATATYPE data)
{
//参数判断
if (!st)
{
fprintf(stderr, "Illegal Stack Address\n");
return;
}
st->top++;
//空间不足则扩容
if ((st->top) >= (st->capacity))
{
StackExpand(st);
}
//入栈
st->data[st->top] = data;
}然后在 main.c 中输入以下,并测试:
StackInit(NULL);
StackInit(&st);
StackPush(&st, 1);
StackPush(&st, 2);
StackPush(&st, 3);
StackPush(&st, 4);
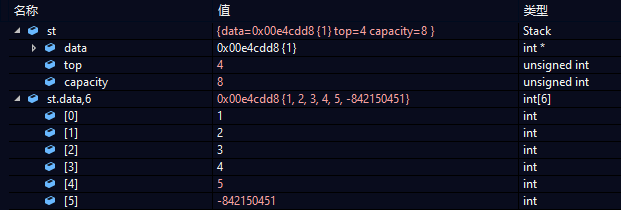
StackPush(&st, 5);![]()
测试无误,进行下一步。
3.2、出栈
入栈等于尾插,那出栈自然就等同于尾删。对于出栈操作需要注意两点,栈是否为空以及空间回收。是否空栈只需判别 top 是否等于 -1 。至于空间回收,顺序表中也有提到,操作逻辑完全一致。
这里为了代码可读性,将空栈判断封装为函数,将空间回收也一并封装为函数。 stack.c 中增加如下代码:
//收缩空间
static void StackContract(Stack* st)
{
//参数判断
if (!st)
{
fprintf(stderr, "Illegal Stack Address\n");
return;
}
DATATYPE* temp = (DATATYPE*)realloc(st->data, sizeof(DATATYPE) * st->capacity / 2);
if (!temp)
{
fprintf(stderr, "Realloc Fail\n");
return;
}
st->data = temp;
st->capacity /= 2;
}
//空表判断 空表返回true
static bool StackIsEmpty(Stack* st)
{
//参数判断
if (!st)
{
fprintf(stderr, "Illegal Stack Address\n");
return true;
}
return (st->top == -1 ? true : false);
}
//出栈
void StackPop(Stack* st)
{
//参数判断
if (!st)
{
fprintf(stderr, "Illegal Stack Address\n");
return;
}
//数据为空直接返回
if (StackIsEmpty(st))
{
fprintf(stderr, "Stack Empty\n");
return;
}
//出栈
st->top--;
//空间过剩则收缩空间
if ((st->top) < (st->capacity) / 2)
{
StackContract(st);
}
}3.3、附加功能
出栈功能写完后,获取栈顶数据及打印输出栈顶数据的功能也一并加上。首先在 stack.h 中进行声明:
//打印
extern void StackPrint(Stack*);
//获取栈顶数据
extern DATATYPE StackGetTopData(Stack*);然后继续在 static.c 中补充这两个功能。
这里需要注意,因为获取栈顶数据是有返回值的,因此如果空表或者传入空指针便不能简单地 return ,容易对返回值的接收产生误解。而不论 return 任何值,均有可能被误以为栈顶数据就是该值,因此这里以 assert 判定最佳:
//获取栈顶数据
DATATYPE StackGetTopData(Stack* st)
{
//参数判断
assert(st);
//空表警告
assert(!StackIsEmpty(st));
//取数据并出栈
DATATYPE data = st->data[st->top];
StackPop(st);
return data;
}
//打印
void StackPrint(Stack* st)
{
//参数判断
if (!st)
{
fprintf(stderr, "Illegal Stack Address\n");
return;
}
//空表打印NULL后返回
if (StackIsEmpty(st))
{
printf("NULL ");
return;
}
//打印栈顶并出栈
printf(DATAPRT " ", StackGetTopData(st));
}至此功能完毕。之后便是测试,同时也顺带测试之前出栈的函数。完整的 main 函数代码:
int main()
{
Stack st;
StackInit(NULL);
StackInit(&st);
StackPush(&st, 1);
StackPush(&st, 2);
StackPush(&st, 3);
StackPush(&st, 4);
StackPush(&st, 5);
StackPrint(&st); //5
StackPrint(&st); //4
StackPrint(&st); //3
StackPrint(&st); //2
StackPrint(&st); //1
StackPrint(&st); //NULL
StackPrint(&st); //NULL
StackPush(&st, 1);
StackPush(&st, 2);
StackPush(&st, 3);
StackPrint(&st); //3
StackDestroy(&st);
StackPrint(&st); //NULL
return 0;
}测试结果如下:
至此栈结构便完成了。
4、以链表实现栈
链表实现栈的文件结构与顺序表实现栈的结构一致,根据以下代码自行测试研究。有链表的基础打底,这里实现起来也将十分轻松:
stack.h :
#include
#include
#include
#include
#define DATAPRT "%d"
typedef int DATATYPE;
typedef struct StackNode
{
DATATYPE data;
struct StackNode* next;
}StackNode;
typedef struct StackInfo
{
StackNode* StackHead;
size_t StackSize;
}StackInfo;
//函数声明---------------------------------
//初始化
extern void StackInit(StackInfo*);
//销毁
extern void StackDestroy(StackInfo*);
//入栈
extern void StackPush(StackInfo*, DATATYPE);
//出栈
extern void StackPop(StackInfo*);
//获取栈顶数据
extern DATATYPE StackGetHead(StackInfo*);
//打印栈顶数据
extern void StackPrint(StackInfo*); stack.c :
#include "stack.h"
//初始化
void StackInit(StackInfo* info)
{
//参数有效判断
if (!info)
{
fprintf(stderr, "Illegal StackInformation Address\n");
return;
}
//初始化
info->StackHead = NULL;
info->StackSize = 0;
}
//销毁
void StackDestroy(StackInfo* info)
{
//参数有效判断
if (!info)
{
fprintf(stderr, "Illegal StackInformation Address\n");
}
//空链表直接返回
if (!info->StackSize)
{
return;
}
//逐节点释放空间
StackNode* currentNode = info->StackHead;
while (currentNode)
{
StackNode* destroyNode = currentNode;
currentNode = currentNode->next;
free(destroyNode);
}
info->StackHead = NULL;
info->StackSize = 0;
}
//判空
static bool StackIsEmpty(StackInfo* info)
{
//参数有效判断
if (!info)
{
fprintf(stderr, "Illegal StackInformation Address\n");
return;
}
return (info->StackSize == 0 ? true : false);
}
//入栈
void StackPush(StackInfo* info, DATATYPE data)
{
//参数有效判断
if (!info)
{
fprintf(stderr, "Illegal StackInformation Address\n");
return;
}
StackNode* newNode = (StackNode*)malloc(sizeof(StackNode));
if (!newNode)
{
fprintf(stderr, "Malloc Fail\n");
return;
}
newNode->data = data;
newNode->next = info->StackHead;
info->StackHead = newNode;
info->StackSize++;
}
//出栈
void StackPop(StackInfo* info)
{
//参数有效判断
if (!info)
{
fprintf(stderr, "Illegal StackInformation Address\n");
return;
}
if (StackIsEmpty(info))
{
fprintf(stderr, "Stack Empty\n");
return;
}
StackNode* destroyNode = info->StackHead;
info->StackHead = info->StackHead->next;
info->StackSize--;
free(destroyNode);
}
//获取栈顶数据
DATATYPE StackGetHead(StackInfo* info)
{
//参数有效判断
assert(info);
//空表警告
assert(!StackIsEmpty(info));
DATATYPE data = info->StackHead->data;
StackPop(info);
return data;
}
//打印栈顶数据
void StackPrint(StackInfo* info)
{
//参数有效判断
if (!info)
{
fprintf(stderr, "Illegal StackInformation Address\n");
return;
}
if (StackIsEmpty(info))
{
printf("NULL ");
return;
}
printf(DATAPRT " ", StackGetHead(info));
}main.c 的测试用例:
#include "stack.h"
int main()
{
StackInfo info;
StackInit(NULL);
StackInit(&info);
StackPush(&info, 1);
StackPush(&info, 2);
StackPush(&info, 3);
StackPush(NULL, 20);
StackPush(&info, 4);
StackPush(&info, 5);
StackPrint(&info);
StackPrint(&info);
StackPrint(&info);
StackPrint(&info);
StackPrint(&info);
StackPrint(&info);
StackPrint(&info);
StackPrint(&info);
StackPush(&info, 1);
StackPush(&info, 2);
StackPush(&info, 3);
StackPrint(&info);
StackDestroy(&info);
StackPrint(&info);
return 0;
}