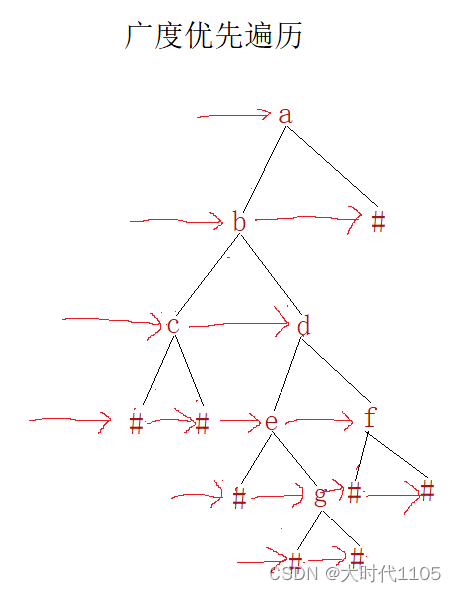
二叉树的链式结构

1.二叉树的构建

想要对二叉树进行操作，我们得先构建一个二叉树

因此，这里的问题就是给定数据，如何将数据在逻辑结构上变成二叉树？

结构定义：

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType val;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

我们想构建上图的二叉树(#代表空)，有两种方式

方法1：手动构建

• 手动创建每一个结点，再手动将它们连起来

BTNode* CreateTreeNode(BTDataType x)
{
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode == NULL)
	{
		perror("CreateTreeNode:malloc fail");
		exit(-1);
	}
	newNode->val = x;
	newNode->left = NULL;
	newNode->right = NULL;

	return newNode;
}

//方法1：手动构建
BTNode* CreateBinaryTree(BTDataType* a)
{
	BTNode* n1 = CreateTreeNode('a');
	BTNode* n2 = CreateTreeNode('b');
	BTNode* n3 = CreateTreeNode('c');
	BTNode* n4 = CreateTreeNode('d');
	BTNode* n5 = CreateTreeNode('e');
	BTNode* n6 = CreateTreeNode('f');
	BTNode* n7 = CreateTreeNode('g');

	n1->left = n2;
	n2->left = n3;
	n2->right = n4;
	n4->left = n5;
	n4->right = n6;
	n5->right = n7;

	return n1;
}

很显然，这种方法不够高效，如果有上百个结点，每个结点都要我们手动去连接，效率实在太低；

我们的第二种方法是给你一个二叉树的前序/中序/后序遍历，用递归去构建二叉树；

当然了，在讲这种方法前，我们得先知道一棵树的前序/中序/后序遍历是什么

---

1.1前序/中序/后序遍历

对于任意一颗二叉树，都有三种遍历，对应着不同的结点访问顺序

• 前序遍历：根->左子树->右子树
• 中序遍历：左子树->根->右子树
• 后序遍历：左子树->右子树->根

可以看到，三种遍历的本质是根结点的访问顺序

• 在以后的题目当中，任何一棵树我们都要分成三部分：根 左子树 右子树
• 前序遍历，先访问根，也就是先将根打印出来，再去递归左子树和右子树
• 中序/后序同理

//前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	printf("%c ", root->val);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	InOrder(root->left);
	printf("%c ", root->val);
	InOrder(root->right);
}

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->val);
}

讲完了二叉树的遍历，就可以试着用递归去构建二叉树了

方法2：递归构建

• 假设一个二叉树的前序遍历”a b c # # d e # g # # f # # # “，根据该结果去构建二叉树，#代表空树
• 用指针pi记录字符串的下标
• 由于是前序遍历，我们的构建顺序为先构建根，再构建左子树和右子树，遇到空pi往后走一步再返回

//方法2：代码自动构建
BTNode* CreateBinaryTree(BTDataType* a, int* pi)
{
	if (a[(*pi)] == '#')
	{
		(*pi)++;
		return NULL;
	}

	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode == NULL)
	{
		perror("CreateBinaryTree:malloc fail");
		exit(-1);
	}
	newNode->val = a[(*pi)++];

	newNode->left = CreateBinaryTree(a, pi);
	newNode->right = CreateBinaryTree(a, pi);

	return newNode;
}

---

2.二叉树的基本操作

2.1求二叉树的结点个数

• 二叉树的结点个数 = 左子树的结点个数 + 右子树的结点个数 + 1

//结点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

---

2.2求二叉树的叶子结点个数

• 如果一个结点的左右子树都为空，则该结点为叶子结点
• 总叶子结点个数 = 左子树叶子节点个数 + 右子树叶子节点个数

//叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	if (root->left == NULL && root->right == NULL)
		return 1;

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

---

2.3求二叉树第k层的结点个数

• 第k层的结点个数 = 左子树的k-1层结点个数 + 右子树的k-1层结点个数

//第k层结点个数
int BinaryTreeKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return BinaryTreeKSize(root->left, k - 1) + BinaryTreeKSize(root->right, k - 1);
}

---

2.4二叉树查找

• 先在当前结点找，如果找不到，再去左子树和右子树找，只要在其中一颗子树中找到了，就直接返回，不需要再往下找了

//查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;

	if (root->val == x)
		return root;

	BTNode* ret1 = BinaryTreeFind(root->left, x);
	if (ret1)
		return ret1;

	BTNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret2)
		return ret2;

	return NULL;
}

---

3.二叉树的层序遍历

3.1层序遍历的定义

上面介绍的前序/中序/后序遍历属于深度优先遍历(DFS)，准确点说前序遍历属于深度优先遍历；

而层序遍历属于广度优先遍历(BFS)

• 深度优先遍历：先访问完左子树在返回去访问右子树

  

• 广度优先遍历：先访问完一层，再去访问下一层

  

3.2层序遍历的实现

• 我们的要求是先打印当前层结点，再打印下一层的结点
• 思路：创建一个队列，对于每一个结点，有两种情况：
  (1)为空，此时什么都不用做(如果想打印空，加个打印即可)
  (2)为正常值，此时将该结点记录下来后出队列，再将该节点的左结点和右节点入队列
  结束条件是队列为空

//层序遍历
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);

	if (root != NULL)
		QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		QDataType front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			printf("%c ", front->val);
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}

    QueueDestroy(&q);
}

如果想打印完一层后换行，再打印下一层，该怎么实现？

• 用一个变量来记录每一层的结点个数，当该变量递减到0，表示该层出完了，换行后赋予变量下次层的结点个数，直到队列为空
• 怎么知道下一层的结点个数呢？当一层的结点出完后，此时队列数据的个数就是下一层的结点数

//层序遍历
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);

	if (root != NULL)
		QueuePush(&q, root);

	int levelSize = 1;

	while (!QueueEmpty(&q))
	{
		while (levelSize--)
		{
			QDataType front = QueueFront(&q);
			QueuePop(&q);

			if (front)
			{
				printf("%c ", front->val);
				QueuePush(&q, front->left);
				QueuePush(&q, front->right);
			}
		}
		printf("\n");
		levelSize = QueueSize(&q);
	}

    QueueDestroy(&q);
}

---

3.3完全二叉树的判断

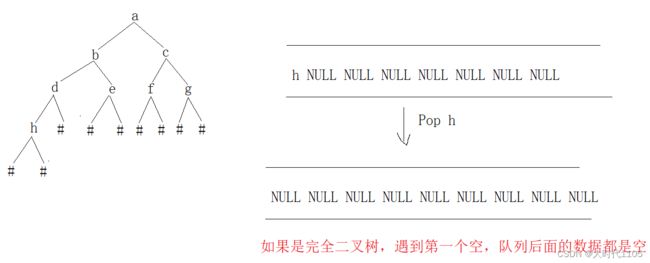
• 思路：同样是利用队列的性质，假如是一个完全二叉树，那么遇到第一个空结点，队列后面的数据就全是空
• 因此判断是不是完全二叉树就变成了判断遇到第一个空时，队列中后面的数据有没有非空结点，如果有，则不是完全二叉树
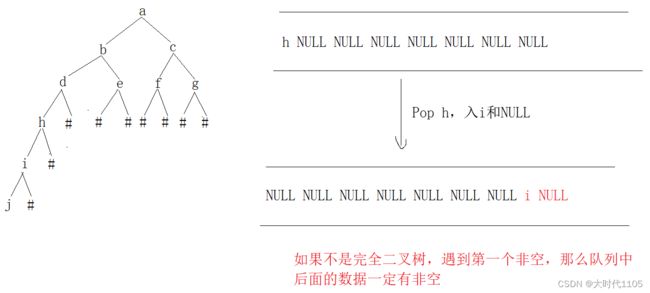
• 有没有这样的可能性，遇到第一个非空时，只是因为二叉树非空数据还没入到队列中才导致队列中后面的数据都是空，而不是该树本身是完全二叉树？答案是不可能
• 我们考虑极端情况

//判断一颗二叉树是否为完全二叉树
bool IsCompleteBinaryTree(BTNode* root)
{
	Queue q;
	QueueInit(&q);

	if (root != NULL)
		QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		QDataType front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			break;
		}
	}

	while (!QueueEmpty(&q))
	{
		QDataType front = QueueFront(&q);
		QueuePop(&q);

		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}

	QueueDestroy(&q);
	return true;
}

---

4.二叉树的销毁

• 这里我们用后序遍历销毁
• 如果用前序/中序遍历销毁，free后root->left或root->right就是野指针了
• 记得在外面将root置空，避免野指针

//二叉树的销毁
void BinaryTreeDestroy(BTNode* root)
{
	if (root == NULL)
		return;

	BinaryTreeDestroy(root->left);
	BinaryTreeDestroy(root->right);
	free(root);
}

---

需要源码的小伙伴可以去我的Gitee主页查看

BInaryTree/BInaryTree · baiyahua/LeetCode - 码云 - 开源中国 (gitee.com)