【贪玩巴斯】每日一练——《力扣：LeetCode 算法入门》（C++）：数组——「旋转图像」 2021-11-26
旋转图像
- 题目：
-
- 题目：旋转图像
- C++源程序：
- 个人心得：
- 涉及知识：
作者：力扣 (LeetCode)
链接：https://leetcode-cn.com/leetbook/read/top-interview-questions-easy/xnhhkv/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
题目：
题目：旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1：
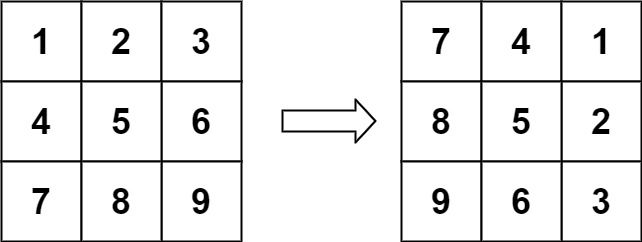
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]
示例 2：
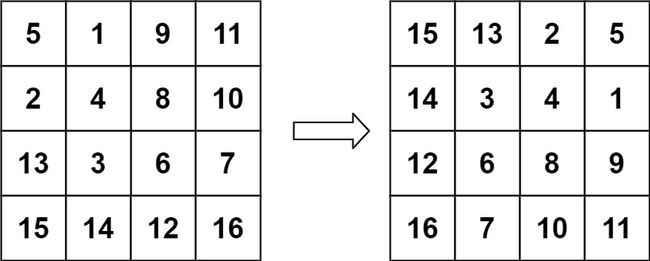输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
示例 3：
输入：matrix = [[1]]
输出：[[1]]
示例 4：
输入：matrix = [[1,2],[3,4]]
输出：[[3,1],[4,2]]
提示：
matrix.length == n
matrix[i].length == n
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000
相关标签
数组
数学
矩阵
C++源程序：
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size(); // 得到外层即二维的个数
auto matrix_new = matrix; // C++ 这里的 = 拷贝是值拷贝，会得到一个新的数组
// i 行 j 列
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
matrix_new[j][n- i -1] = matrix[i][j]; // 直接思维——即90°转换赋值 比如matrix[0][2] ——>90°变换 matrix[2][n-i-1] 关键就是要想到[ n - i - 1] 这个规律。这个规律建议大家通过画图来推理研判。
}
}
matrix = matrix_new; // 拷贝
}
};
个人心得：
本题最开始阅读的时候，觉得有思路，但是没有具体的用笔来演化，很明显看出来旋转90°的规律，但是没有具体和程序结合起来思考，没有和程序数组的下标结合起来思考！
之后看了官方题解，才有了具体的下笔方向。
其实就是要落实到具体的下标上去演示，就会发现下标之间有规律，有了规律之后就可以直接复制成新数组！最后再用新数组赋值到要求的数组上输出即可。
涉及知识：
- auto
C++11 auto可以在声明变量的时候根据变量初始值的类型自动为此变量选择匹配的类型，类似的关键字还有decltype。
举个例子：
int a = 10;
auto au_a = a;//自动类型推断，au_a为int类型
cout << typeid(au_a).name() << endl;
输出为 int
auto的自动类型推断发生在编译期，所以使用auto并不会造成程序运行时效率的降低。例如上面的代码，编译的时候，就会把a变量转换为int类型。
auto和其他变量类型有明显的区别：
1.auto声明的变量必须要初始化，否则编译器不能判断变量的类型。
2.auto不能被声明为返回值，auto不能作为形参，auto不能被修饰为模板参数
例子2：
for (std::vectorstd::string::iterator i = vs.begin(); i != vs.end(); i++)
使用auto之后：
for (auto i = vs.begin(); i != vs.end(); I++)
for循环中的i将在编译时自动推导其类型，而不用我们显式去定义那长长的一串。
- 深拷贝浅拷贝问题
很负责，有想法的同学可以查查资料。
这里简单来讲就是因为是用的vector模板，然后直接 = 就可以表示是深拷贝（值拷贝），不需要自己再写了。
深拷贝的话就是开辟了一个新的内存段来存储值。
浅拷贝（shallowCopy）只是增加了一个指针指向已存在的内存地址，
深拷贝（deepCopy）是增加了一个指针并且申请了一个新的内存，使这个增加的指针指向这个新的内存，
使用深拷贝的情况下，释放内存的时候不会因为出现浅拷贝时释放同一个内存的错误。
浅复制：仅仅是指向被复制的内存地址，如果原地址发生改变，那么浅复制出来的对象也会相应的改变。
深复制：在计算机中开辟一块新的内存地址用于存放复制的对象。