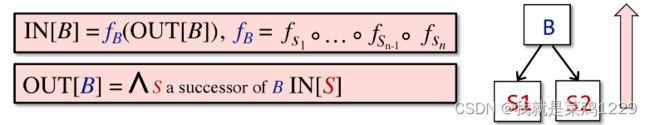南京大学-软件分析-课程03-数据流分析
1. Overview of Data Flow Analysis
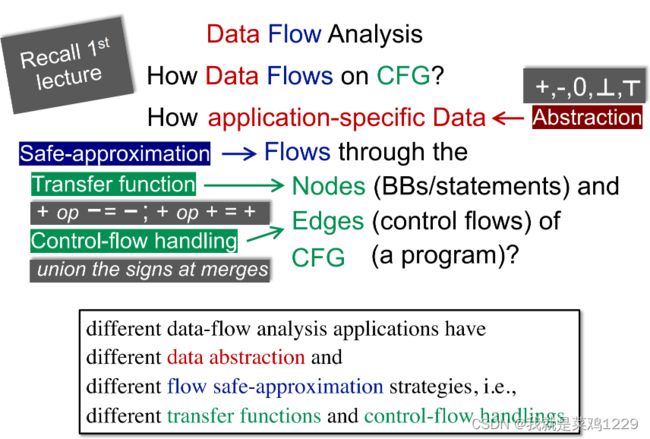
Data如何在CFG上流动？
应用程序特定的数据是如何通过 CFG（程序的控制流图）的节点（基本块/语句）和边（控制流）流动的。
may analysis:
outputs information that may be true (over-approximation)
must analysis:
outputs information that must be true (under-approximation)
这两种逼近的方式都是安全的分析。
2. Preliminaries of Data Flow Analysis
2.1 输入和输出状态
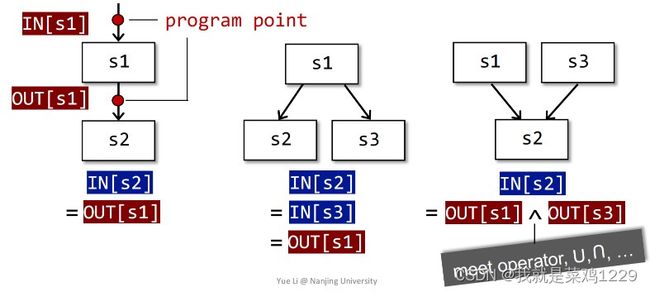
2.2 控制流约束的符号表示 , f B = f s n 。 f s n − 1 … 。。 f s 1 I N [ B ] = ∧ P a p r e d e c e s s o r o f B O U T [ P ] IN[B] = IN[s_1]\\ OUT[B] = OUT[s_n]\\ OUT[B] = f_B(IN[B]), f_B = f_{s_n} 。 f_{s_{n-1}} …。 。f_{s_1}\\ IN[B] = \wedge _{P \ a\ predecessor\ of\ B}\ OUT[P] IN[B]=IN[s1]OUT[B]=OUT[sn]OUT[B]=fB(IN[B]),fB=fsn。fsn−1…。。fs1IN[B]=∧P a predecessor of B OUT[P]
交汇点上使用meet运算符对不同路径的贡献进行总结。
对于反向来说：
3. Reaching Definitions Analysis（可达性分析）
程序点p上的定义d到达点q，如果存在一条从p到q的路径，使得在该路径上d没有被“杀死”。
3.1 抽象
将程序中的每一个定义抽象成一个bit，第i个bit代表定义Di。
如何safe-approximation
3.2 转移方程
这个语句“生成”了变量v的一个定义D，并“杀死”程序中定义变量v的所有其他定义，同时保留了其余的输入定义不受影响。
O U T [ B ] = g e n B ∪ ( I N [ B ] − k i l l B ) OUT[B]=gen_B \cup (IN[B]-kill_B) OUT[B]=genB∪(IN[B]−killB)
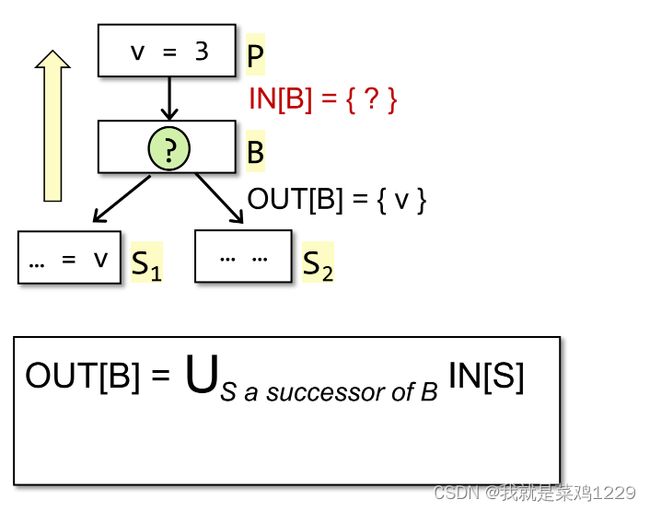
3.3 控制流
I N [ B ] = U P a p r e d e c e s s o r o f B O U T [ P ] IN[B] = U_{P\ a\ predecessor\ of\ B }OUT[P] IN[B]=UP a predecessor of BOUT[P]
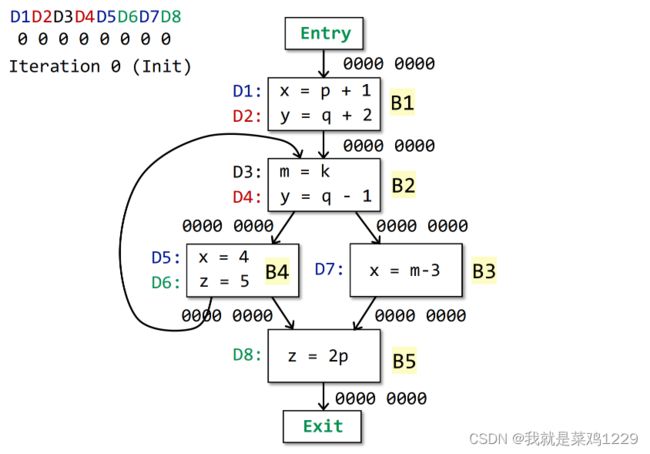
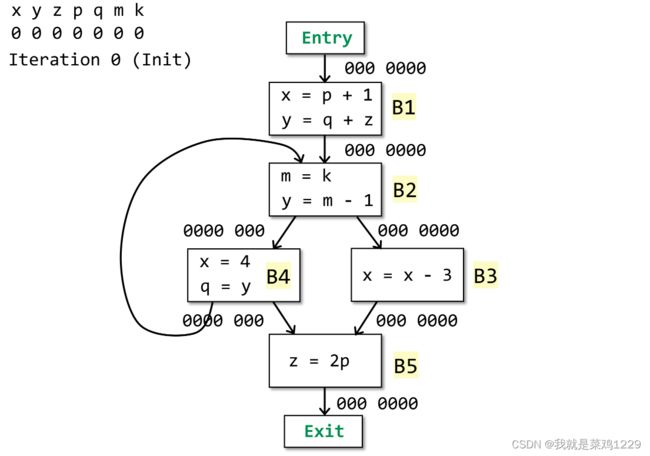
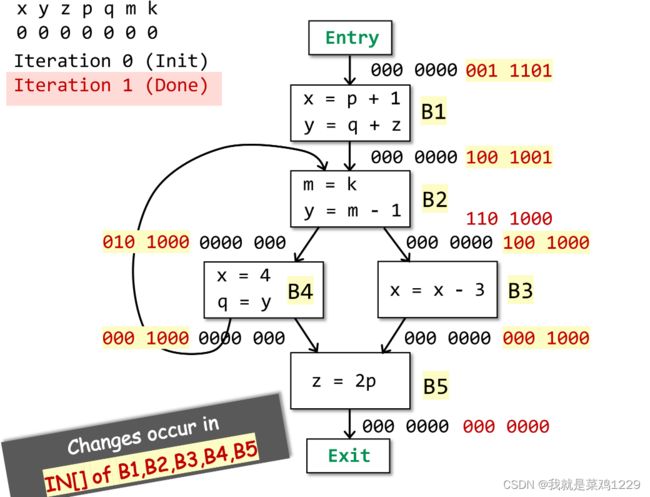
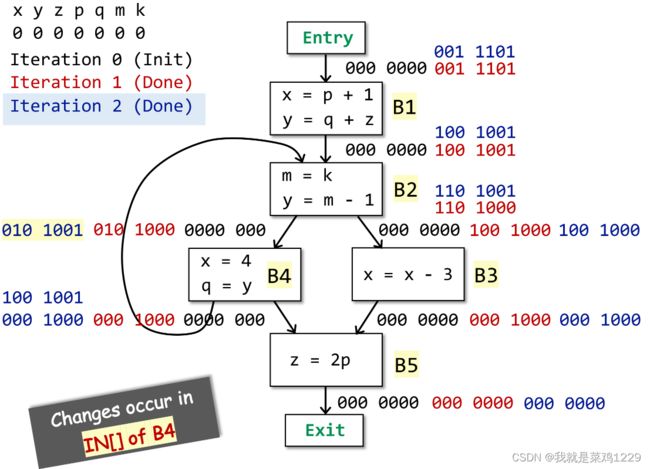
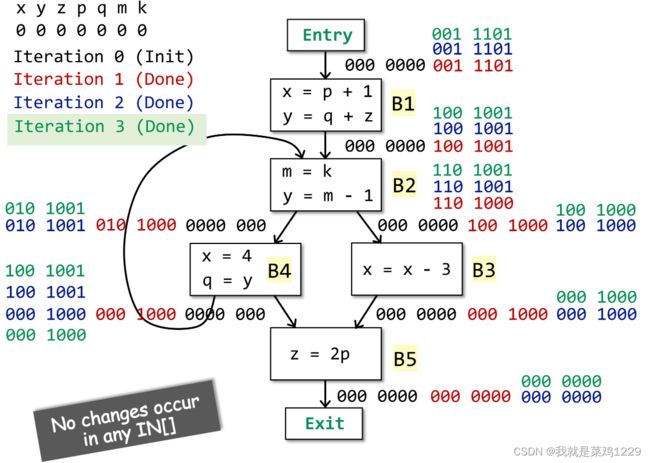
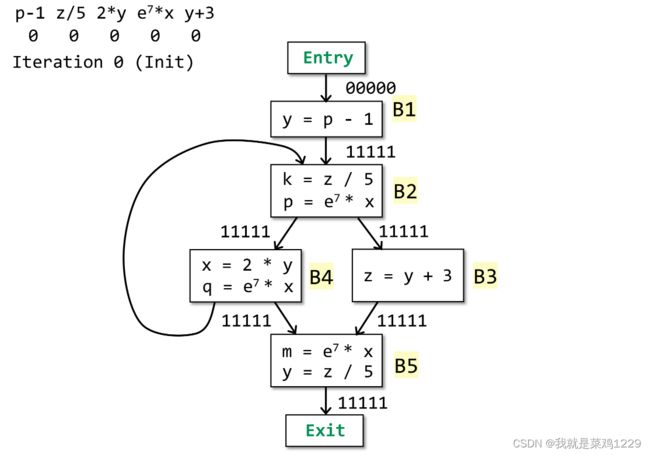
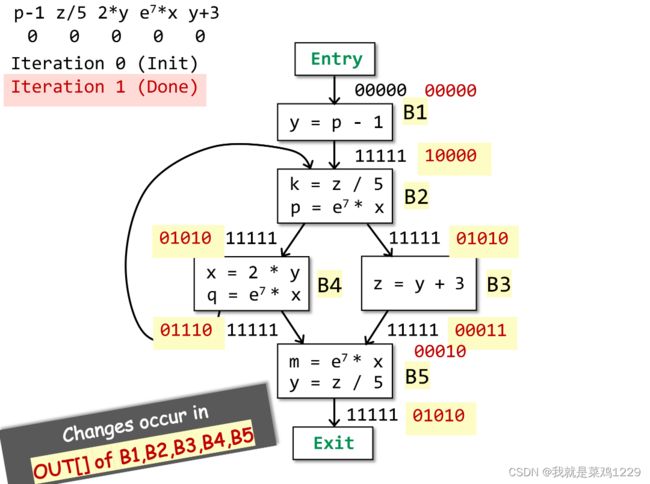
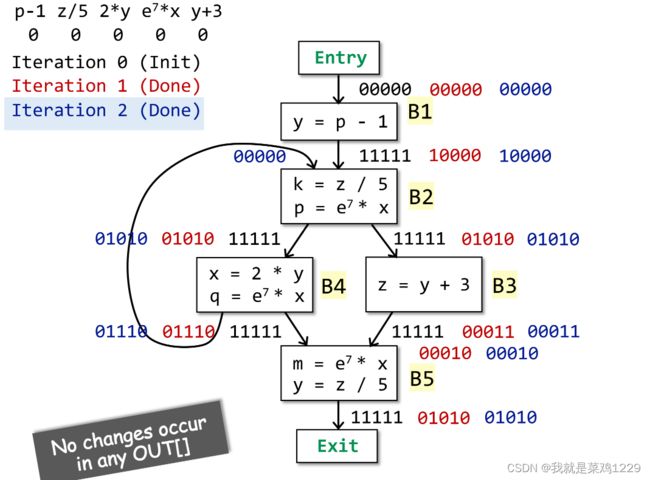
3.4 算法设计
循环的时候排除了entry节点。
3.4.1 初始化
3.4.2 迭代开始
直到输出结果不发生变化为止：
4. Live Variables Analysis（活跃变量分析）
活跃变量分析告诉我们变量 v 在程序点 p 处的值是否可能沿着控制流图（CFG）中从 p 开始的某条路径被使用。如果是这样，v 在 p 处是存活的；否则，在 p 处是死的。
活跃变量的信息可以用于寄存器分配。例如，在某个时刻，所有寄存器都已满，我们需要使用一个寄存器，那么我们应该优先选择使用一个包含死值的寄存器。
4.1 抽象
将程序中的所有变量用bit数组来代表，一个bit代表一个变量。
4.2转换方程
使用backward传递。
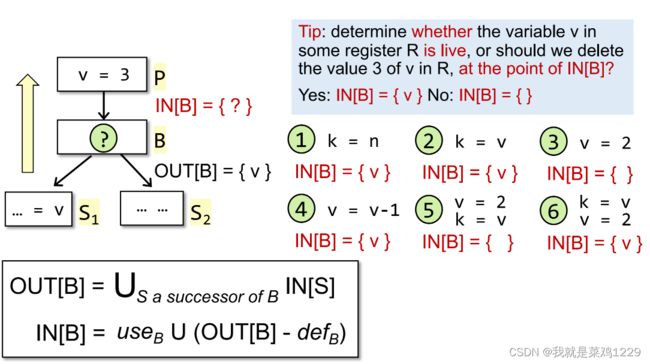
d e f B def_B defB代表在B中被再次定义的变量
u s e B use_B useB代表在B中被重定义之前使用的变量
O U T [ B ] OUT[B] OUT[B]代表在B中一直存活且没有被重定义的
4.3 控制流
B的输出等于所有B的后继节点的输入的并集。
4.4 算法设计
4.4.1 初始化
4.4.2 迭代
5. Available Expressions Analysis
是一个Must Analysis。
5.1 抽象
将程序中所有的表达式进行抽象。每个表达式用一个bit来抽象。
5.2 转换方程
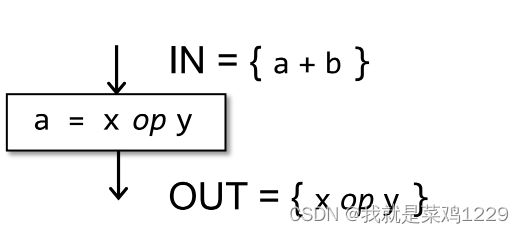
基本块中含有新的表达式a+b。
但是赋值给了一个变量a，kill了原有的表达式a+b。
O U T [ B ] = g e n B ∪ ( I N [ B ] − k i l l B ) OUT[B]=gen_B \cup(IN[B]-kill_B) OUT[B]=genB∪(IN[B]−killB)
5.3 控制流
I N [ B ] = ∩ P a p r e d e c e s s o r o f B O U T [ P ] IN[B]=\cap_{P\ a\ predecessor \ of\ B}OUT[P] IN[B]=∩P a predecessor of BOUT[P]
5.4 算法设计
5.4.1 初始化
5.4.2 迭代
6. Analysis Comparison
三种方法的比较。
| Reaching Definitions | Live Variables | Available Expressions | |
|---|---|---|---|
| Domain | Set of definitions | Set of variables | Set of expressions |
| Direction | Forwards | Backward | Forwards |
| May/Must | May | May | Must |
| Boundary | OUT[entry]=0 | IN[exit]=0 | OUT[entry]=0 |
| Initialization | OUT[B]=0 | IN[B]=0 | OUT[B]=1 |
| Transfer function | OUT = gen U (OUT - kill) | IN = gen U (IN - kill) | OUT = gen U (OUT - kill) |
| Meet | U | U | ∩ \cap ∩ |