第3章 表、栈和队列

3.4 队列ADT

        像栈一样，队列(queue)也是表。然而，使用队列时插入在一端进行而删除则在另一端
进行。

3.4.1 队列模型

队列的基本操作是Enqueue(入队)一它是在表的末端(叫作队尾(rear))插入一个元素，还有Dequeue(出队)——它是删除(或返回)在表的开头(叫作队头(front))的元素。图3-56显示一个队列的抽象模型。

3.4.2 队列的数组实现

        如同栈的情形一样，对于队列而言，任何表的实现都是合法的。像栈一样，对于每一种操作，链表实现和数组实现都给出快速的运行时间。队列的链表实现简单明了，留作练习。现在我们讨论队列的数组实现。
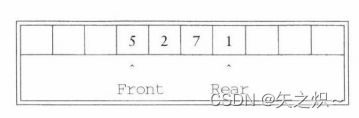
        对于每一个队列数据结构，我们保留一个数组Queue[]以及位置Front和Rear，它们代表队列的两端。我们还要记录实际存在于队列中的元素的个数size。所有这些信息是作为一个结构的一部分，除队列例程本身外通常不会有例程直接访问它们。下图表示处于某个中间状态的一个队列。顺便指出，图中那些空白单元有着不确定的值。尤其是前三个单元含有曾经属于该队列的元素。

        为了使一个元素X入队，我们让Size和Rear增1，然后置Queue[Rear]=X。若使一个元素出队，我们置返回值为Queue[Front]，Size减1，然后使Front增1。也可能有其他的策略(将在后面讨论)。现在论述错误的检测。这种实现存在一个潜在的问题。经过10次入队后队列似乎是满了，因为Rear现在是10，而下一次再入队就会是一个不存在的位置。然而，队列中也许只存在几个元素，因为若干元素可能已经出队了。像栈一样，即使在有许多操作的情况下队列也常常不是很大。
        简单的解决方法是，只要Front或Rear到达数组的尾端，它就又绕回到开头。下图显示在某些操作期间的队列情况。这叫作循环数组(circular array)实现。
        实现回绕所需要的附加代码是极小的(虽然它可能使得运行时间加倍)。如果Front或Rear增1后超越了数组规定的大小，那么其值就要重置为数组的第一个位置。

        关于队列的循环实现，有两件事情要警惕。第一，检测队列是否为空是很重要的，因为当队列为空时，一次Dequeue操作将不知不觉地返回一个不确定的值。第二，某些程序设计人员使用不同的方法来表示队列的队头和队尾。例如，有些人并不用一个单元来表示队列的大小，因为他们依靠的是基准情形，即当队列为空时Rear=Front-1。队列的大小是通过比较Rear和Front隐式算出的。这是一种非常隐秘的方法，因为存在某些特殊的情形，因此，如果你需要修改用这种方式编写的代码，那么就要特别仔细。如果队列的大小不是结构的一部分，那么若数组的大小为ASize，则当存在ASize-1个元素时队列就满了，因为只有ASize个不同的大小值可区分，而0是其中的一个。采用任意一种你喜欢的风格，但要确保你的所有例程都是一致的。由于队列的实现方法有多种选择，因此如果你不使用size字段，那就有必要在代码中插入一些注释。

        在Enqueue的次数肯定不会大于队列的大小的应用中，使用回绕是没有必要的。像栈一样，除非主调例程肯定队列非空，否则Dequeue很少执行。因此对这种操作，只要不是关键的代码，错误的调用常常被跳过。一般说来这并不是无可非议的，因为你可能得到的时间节省量是极小的。
我们通过编写某些队列的例程来结束本节，其余例程留作练习。首先，在图3-57中给出队列的声明。正如对于栈的数组实现所做的那样，我们添加一个最大大小的域。还需要提供例程CreateQueue和DisposeQueue。此外，我们还需要提供测试一个队列是否为空的例程以及构造一个空队列的例程(见图3-58和图3-59)。读者可以编写函数IsFull，用于实现判断队列是否满了的功能。注意，Rear在Front之前预初始化为1。我们将要编写的最后的操作是Enqueue例程。严格遵循上面的描述，图3-60展示了队列的数组实现。

#ifndef _Queue_h

struct QueueRecord;
typedef struct QueueRecord *Queue;

int IsEmpty(Queue Q);
int IsFull(Queue Q);
Queue CreateQueue(int MaxElements);
void DisposeQueue(Queue Q);
void MakeEmpty(Queue Q);
void Enqueue(ElementType X, Queue Q);
ElementType Front(Queue Q);
void Dequeue(Queue Q);
ElementType FrontAndDequeue(Queue Q);

#endif   /*_Queue_h*/

#define MinQueueSize (5)

struct QueueRecord
{
    int Capacity;
    int Front;
    int Rear;
    int Size;
    ElementType *Array;
};

int IsEmpty(Queue Q)
{
    return Q->Size == 0;
}

void MakeEmpty(Queue Q)
{
    Q->Size = 0;
    Q->Front = 1;
    Q->Rear = 0;
}

static int Succ(int Value, Queue Q)
{
    if (++Value == Q->Capacity)
        Value = 0;
    return Value;
}

void Enqueue(ElementType X, Queue Q)
{
    if (IsFull(Q))
        Error("Full queue");
    else
    {
        Q->Size++;
        Q->Rear = Succ(Q->Rear, Q);
        Q->Array[Q->Rear] = X;
    }
}

3.4.3 队列的应用

        有几种使用队列来提高运行效率的算法。它们当中有些可以在图论中找到，我们将在第9章讨论它们。这里，先给出某些应用队列的例子。

        当作业送交给一台行式打印机，它们就按照到达的顺序排列起来。因此，送往行式打印机的作业基本上被放到一个队列中。

        实际生活中的每次排队都(应该)是一个队列。例如，在一些售票口排列的队都是队列，因为服务的顺序是先到的先买票。

        另一个例子是关于计算机网络的。有许多种PC网络设置，其中磁盘是放在一台叫作文件服务器的机器上的。使用其他计算机的用户是按照先到先使用的原则访问文件的，因此其数据结构是一个队列。

        进一步的例子如下：

• 当所有的接线员忙得不可开交的时候，对大公司的传呼一般都被放到一个队列中。
• 在大学里，如果所有的终端都被占用，由于资源有限，学生们必须在一个等待表上签字。在终端上登录时间最长的学生将首先被强制离开，而等待时间最长的学生则将是下一个被允许使用终端的用户。

        处理用概率的方法计算用户排队预计等待时间、等待服务的队列能够排多长，以及其他一些诸如此类的问题将用到被称为排队论(queueing theory)的完整数学分支。问题的答案依赖于用户加入队列的频率以及一旦用户得到服务时处理服务花费的时间。这两个参数作为概率分布函数给出。在一些简单的情况下，答案可以解析算出。一种简单的例子是一条电话线有一个接线员。如果接线员忙，打来的电话就被放到一个等待队列中(这还与某个容许的最大限度有关)。这个问题在商业上很重要，因为研究表明，人们会很快挂上电话。

        如果我们有k个接线员，那么这个问题解决起来要困难得多。解析求解困难的问题往往使用模拟的方法求解。此时，我们需要使用一个队列来进行模拟。如果k很大，那么我们还需要其他一些数据结构来使得模拟更有效地进行。在第6章将会看到模拟是如何进行的。那时我们将对k的若干值进行模拟并选择能够给出合理等待时间的最小的k。

        正如栈一样，队列还有其他丰富的用途，这样一种简单的数据结构竟然能够如此重要，实在令人惊奇。