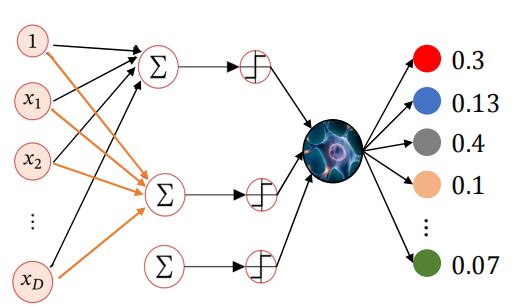
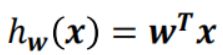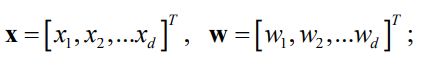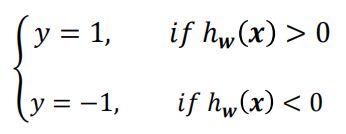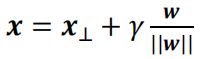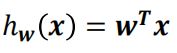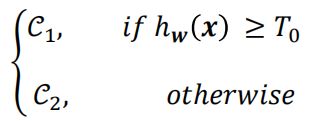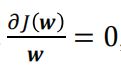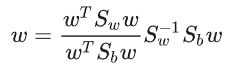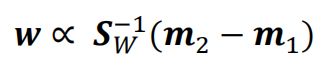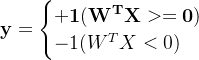Linear classifiers——线性分类器

1.(Generalized) Linear classifiers——广义线性分类器

1.1 模型

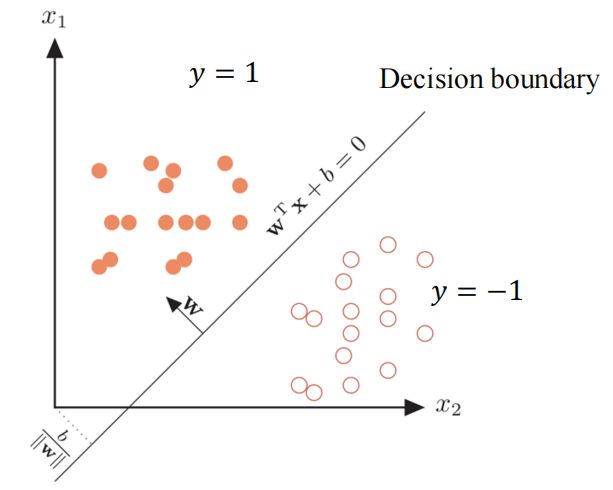
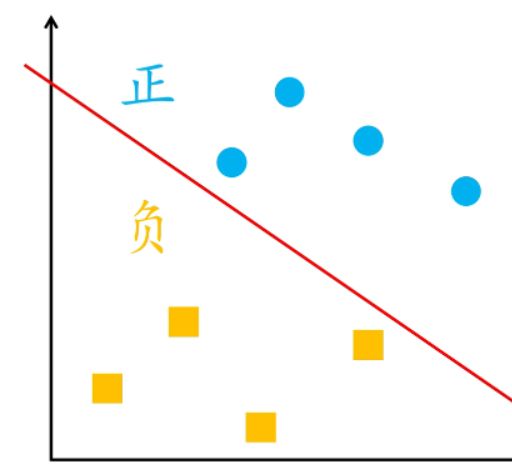
        假如有两类数据，类别标签为y = 1和y = -1

        我们可以使用一个线性函数将其分类，二维形式

                                        

        通常x增加一个恒等于1的维度，可以将b合并进w，于是更一般的形式为

                                         

                

                ,就相当于b

        输出分类标签

                                

1.2 几何意义

        对于，其法向量为,单位化

对于平面上的一个数据点的向量来说，可以被分解为如下

                                            

        其中表示向量x在决策函数上的投影向量，γ表示x到决策边界的距离，那么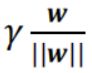就表示x垂直决策边界的向量

                                        

        由点到面的距离公式可得，x到决策函数的距离

                        

        变形得

                        

        决策函数的正负了反映数据点的类别，而且其大小也反映了数据点到决策边界距离

2.Fisher’s linear discriminant——Fisher’s 线性判别

1.Fisher’s 线性判别的原理

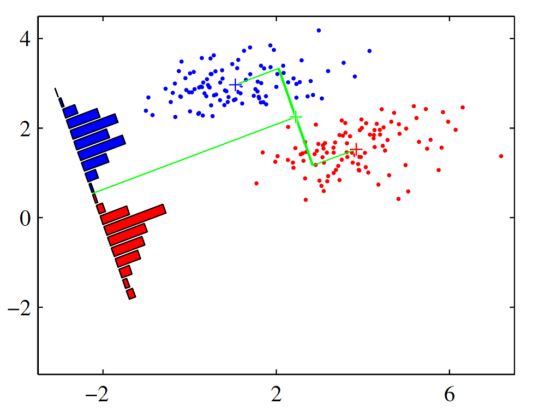
        Fisher’s 线性判别通过降维的方式进行两类别分离，将高纬度的数据在低纬度上进行投影。投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大，也就是“类内小，类间大”。

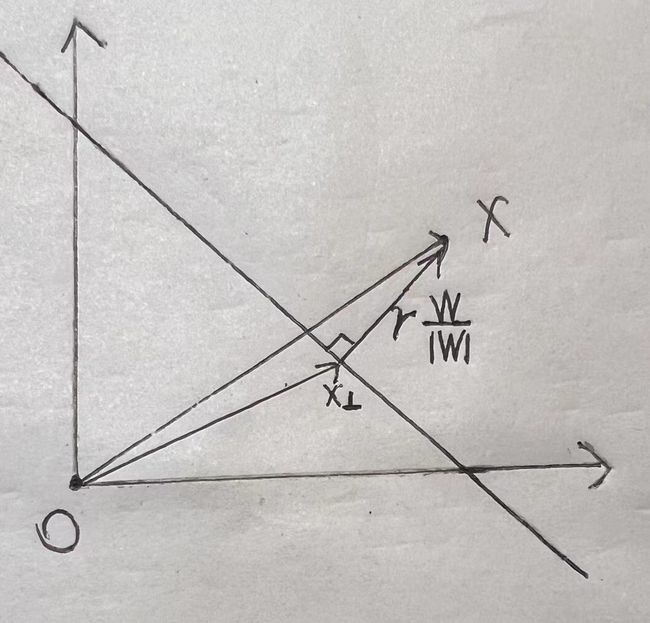
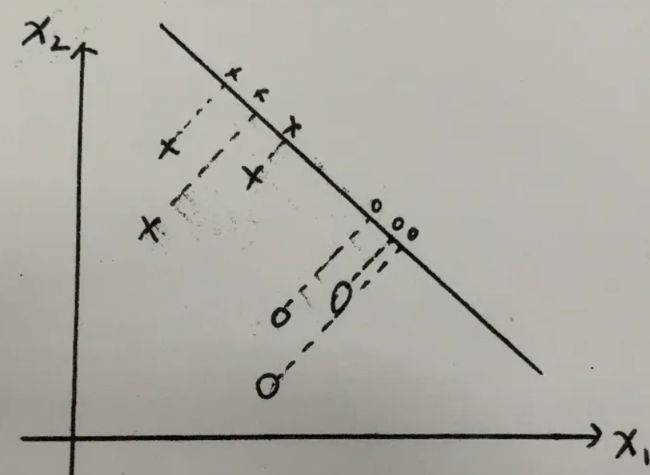
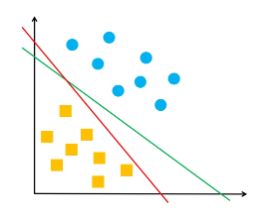
        例有两类数据“x”"o",二维的数据降维就是投影到一条直线上

               

        选取不同的投影轴，会产生不同的效果，很明显第一张图效果就比第二张图好,所以只需要找到一个满足需求的W向量就能实现分类任务。

2.Fisher’s 线性判别的推导

        假设投影到w向量上，同时限定|w|=1,拥有两个特征的数据点向量投影到向量w上等于(w相当于一个新的坐标轴，通过投影在w轴上的获得的值)

证明：

在w上的投影长度为y=

         于是我们可以建立

                                                        

        通过1.可知，数据点会分布在w上的不同位置，通过设定一个阈值完成分类

                                        

        假设我们有两个类别和，分别有和个数据

        可以计算出两类数据的均值，通过均值的差距来表现类间的差距

                 ,

                 

        同样可以计算出两类数据的方差，通过方差来表现类内的差距

                

                

        根据“类内小，类间大”的思想，我们可以建立如下目标函数

                ，与类间均值成正比，类内方差成反比

  

        

令,表示类间协方差矩阵

令,表示类内协方差矩阵

        可以得到

                

        这个就是损失函数，目标是求最大值

       对w求偏导 有（这里需要用到矩阵求导）

        

           

        假设数据点有p维

最终我们可以得到

                                

                

• 求解速度快，不需要像SGD一样迭代，简单高效
• 对于数据的特征维度不能太高<1000

3.Perceptron——感知机

3.1 感知机及其模型

        感知机是一个二分类线性模型

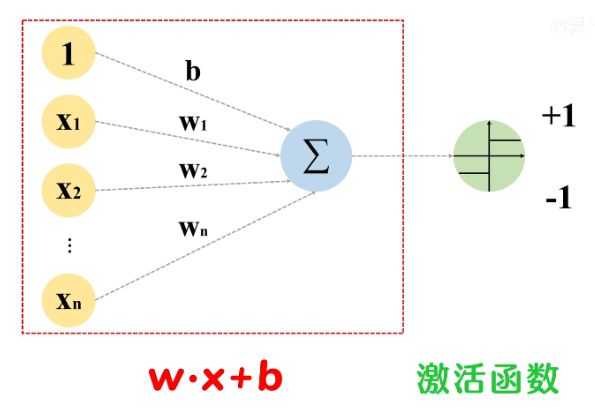
        对于每个输入数据x都会有一个对应的权重w，图中的○称为“神经元”或者“节点”。

        输入被送往神经元时，会被分别乘以固定的权重加上偏置项 （wx+b），神经元会计算传送过来的信号的总和，在经过一个非线性激活函数输出最终的值，在感知机中使用的是符号函数sign。

                        

        如果用X表示特征向量，W表示权重向量（按照之前同样的方法把b并入W向量），最终该模型可以表示为

                                

        决策边界为,产生一个线性分割超平面

        

3.2 损失函数

         我们很容易想到的一个损失函数的是误分类点的总数，但是这样损失函数与w无关，不是参数w和b的连续可导函数导函数导函数，无法得到w的值。

          于是，感知机采用误分类点到超平面的总距离,如下图              

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

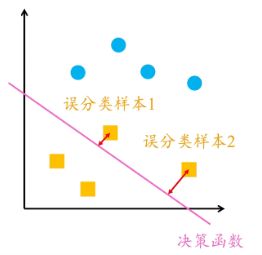
        单个样本到超平面的距离如下公式

        ​​​​​​​        ​​​​​​​         ​​​​​​​   ()

        对于每一个误分类样本来说，都有成立，其中为真实标签，下面给出证明：

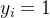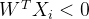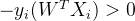• 当时，误分类样本,可以得到,且此时有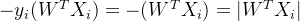
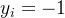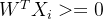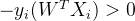• 当时，误分类样本,可以得到，且此时有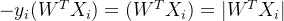

        于是误分类点到超平面的总距离可以表示为下式：
                ，M表示误分类点集合

        此外，1/||w||用来归一化超平面法向量，得到几何间隔，也就是点到超平面的距离，但超平面只要能够将两类样本分类开即可,距离大小没关系，下图中两条决策边界都是正确的 

                                        

        最终感知机损失函数为

                

3.3 梯度下降

        对于感知机来说，极小化过程中不是一次使M中所有误分类点的梯度下降，而是一次随机选取一个点使其梯度下降，因此感知机的优化器使用的是随机梯度下降（SGD）。

        当选取的点分类正确时，无需进行参数更新

        当选取的点分类错误时

                计算该点损失函数的梯度:

                ​​​​​​​        

                更新W

                        

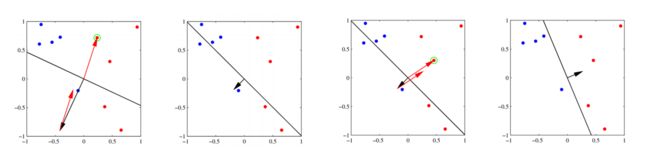
                同时可以看出，当一个误分类点的真实标签为1时即=1时，W在原本基础上增加了一个X，当一个误分类点的真实标签为1时即=-1时，W在原本基础上减少一个X，如下图

3.4 代码实现

        一个二维的感知机，决策边界为y=wx+b

# 训练参数
epochs = 100
η = 0.1
 
# 感知机
def perceptron(X, y, η, epochs):
    n_samples, n_features = X.shape
    # 初始化权重参数
    w = np.zeros(n_features)
    b = 0
    for epoch in range(epochs):
        for i in range(n_samples):
            # 预测值
            y_pred = 1 if (np.dot(X[i], w) + b) > 0 else -1            
            # 随机梯度下降法随机选择一个误分点进行参数更新
            if -y[i]*(np.dot(X[i], w) + b)>=0:
                w = w + η * X[i] * y[i]
                b = b + η * y[i]
                loss += 1
    return w, b
 
# 预测函数
def predict(X,w):
    y_pred = np.where(np.dot(X,w)+b>0,1,-1)
    return y_pred
 
w,b = perceptron(trainx,trainy,η,epochs)

4.Softmax regression

4.1 Softmax regression模型

        Softmax regression是逻辑回归的推广，是一个多类别分类器。分类类别需要转化为one-hot编码，如下图所示

奶牛的one-hot编码为（1，0，0）1和0表示属于某一类的概率

        对于每一个分类都有其对应W向量，输入特征向量X，假设K分类问题，输入X先经过线性回归得到K个

                ​​​​​​​,j=1,2,……K，

        接着通过一个Softmax函数，这个函数会把输入都映射到[0,1]之间，就可以得到输入X对于K个分类各自的概率

                (y=i，表示第i个类别)

        ​​​​​​​        ​​​​​​​

        最终模型的预测

                ，取概率最大的类别

        附上一个四分类的计算例子

       由 可以得出，所有分类概率之和恒等于1

4.2 交叉熵损失函数（cross-entropy）

        

其中:

• N是样本数量
• K是类别数量
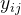•  是第i个样本中第j个类别的真实标签值
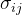• 是模型预测的第个样本中第j个类别的概率

        这个损失函数涉及两个求和符号。外层求和对应于所有的样本，内层求和对应于每个样本中各个类别的交叉熵损失

4.3 梯度下降

第j个分类的权重向量：

更新参数