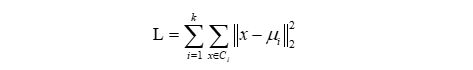【YOLO系列】 速看!YOLOv3中如何使用K-Means聚类算法生成Anchor Box
一、背景
我们在YOLO V2中说到,在Faster RCNN中anchor boxes大小都是手动设定的,这就带有一定的主观性,会使得网络在使用中不能更好的做出预测。这是在使用anchor boxes出现的第一个问题。为了解决这个问题,于是YOLO V2提出了使用k-Means聚类方法在训练集中自动的获取每个anchor boxes的大小,以替代人工设置。
k-Means算法的思想很简单,对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。然后使每个簇内的点离中心点尽量近,让簇间的距离尽量远。
用公式来表示,则为最小化平方误差L:
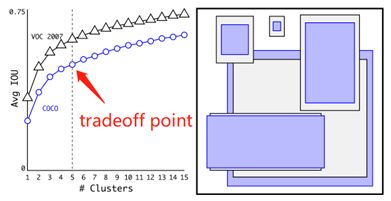
但是如果直接使用k-Mean的欧氏距离来度量进行聚类的话,结果会导致大的box比小的box产生更大的误差。而在YOLO V2中使用聚类的目的是为了使得anchor boxes和Ground Truth有更大的IOU,因此这就和anchor boxes的尺寸大小没有直接的关系。所以将使用以下的公式来进行度量:
d(box, centroid) = 1-IOU(box, centroid)
到聚类中心的距离越小越好,即IOU值越大越好。
但是呢,YOLO V2虽然提出了这个方法,它却没有用到YOLO V2中,原因是mAP降低了。于是这个方法真正是在YOLO V3中使用的。
二、实现过程
根据上述内容,产生Anchor Box的核心内容可以简述为
1、Kmeans聚类
2、IOU
1、K-Means
(1)K-means聚类的步骤可以简述如下:
a. 随机选择k个类别的中心点。
b. 对任意一个样本,求其到各类中心的距离(欧式距离,此处替换为IOU计算),将该样本归到距离最短的中心所在的类。
c. 聚好类后,重新计算每个聚类的中心点位置。
d. 重复b、c步骤迭代,直到k个类中心点的位置不变,或者达到一定的迭代次数,则迭代结束,否则继续迭代。
(2)代码实现
def kmeans(self, boxes, k, dist=np.median):
box_number = boxes.shape[0] # 获取boxes的行数,也就是有多少个GT框
distances = np.empty((box_number, k)) # 创建一个 box_number行 ,k列的空矩阵
last_nearest = np.zeros((box_number,)) # 创建一个 box_number行的零矩阵
np.random.seed() # 设置随机数生成器的种子
clusters = boxes[np.random.choice(
box_number, k, replace=False)] # 初始化 k clusters, 在boxes中随机选择k个框的宽高,作为9个类的初始中心, replace = False 代表不允许重复选择
while True:
distances = 1 - self.iou(boxes, clusters) # 用1-IOU值来表示anchor boxes和Ground Truth的重叠度,(n,k)
current_nearest = np.argmin(distances, axis=1) # 选择每一行中的最小值,输入该值的索引值,(n,)
if (last_nearest == current_nearest).all(): # 判断当先的类簇中心是否变化
break # clusters won't change
for cluster in range(k): # 更新k个clusters的中心,选择每个簇的中位数为当前的中心
clusters[cluster] = dist( # update clusters
boxes[current_nearest == cluster], axis=0)
last_nearest = current_nearest
return clusters
2、IOU
(1)IOU(Intersection over Union)是目标检测中使用的一个概念,用于衡量预测的边界框与真实的边界框之间的重叠程度。IOU的值介于0到1之间,其中OU=0表示两个边界框没有重叠,IOU=1表示两个边界框完全重叠。IOU的求解步骤简述如下:
a. 计算预测的边界框(预测框)与真实的边界框(标注框)的交集。交集是指两个边界框在空间上重叠的部分。
b. 计算两个边界框的并集。并集是指两个边界框在空间上覆盖的部分。
c. 计算交集与并集的比值,即Intersection over Union(IOU)。IOU等于交集的面积除以并集的面积。
(2)代码实现
def iou(self, boxes, clusters): # 1 box -> k clusters
n = boxes.shape[0] # 获取boxes的行数,也就是有多少个GT框
k = self.cluster_number
box_area = boxes[:, 0] * boxes[:, 1] # 计算GT框的面积,得到(n, )的数组
box_area = box_area.repeat(k) # box_area数组的每个数重复k次,得到(k*n, )的数组
box_area = np.reshape(box_area, (n, k)) # 将repeat得到的(k*n,)的数组,转成(n,k)的数组
cluster_area = clusters[:, 0] * clusters[:, 1] # 计算每个类簇中心框的面积,得到(k, )的数组
cluster_area = np.tile(cluster_area, [1, n]) # 数组的每个数在行的方向重复n次,得到(k*n,)的数组
cluster_area = np.reshape(cluster_area, (n, k)) # 将得到的(,k*n)的数组,转成(n,k)的数组
box_w_matrix = np.reshape(boxes[:, 0].repeat(k), (n, k)) # 先将GT的width重复k次,得到(n*k,)的数组,然后在转成(n,k)的数组
cluster_w_matrix = np.reshape(np.tile(clusters[:, 0], (1, n)), (n, k)) # 先将每个类簇中心的width重复k次,得到(n*k,)的数组,然后在转成(n,k)的数组
# 选择出每个最小width的框。这里要注意一下,这里的对比是没有坐标的概念,也就是说每个框的对比都是默认他们有一个顶点是重合的,然后选出最小的width即可。
min_w_matrix = np.minimum(cluster_w_matrix, box_w_matrix)
# 与上面的操作一样,选择出最小的height
box_h_matrix = np.reshape(boxes[:, 1].repeat(k), (n, k))
cluster_h_matrix = np.reshape(np.tile(clusters[:, 1], (1, n)), (n, k))
min_h_matrix = np.minimum(cluster_h_matrix, box_h_matrix)
inter_area = np.multiply(min_w_matrix, min_h_matrix) # 重叠部分的面积计算
result = inter_area / (box_area + cluster_area - inter_area) # IOU计算=重叠面积/(GT面积+中心面积-重叠面积)
return result