07数论算法练习题解析
数论算法练习题解析
01计数质数
问题描述
给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。
0 <= n <= 5 * 10^6
输入描述
输入一个整数表示 n
输出描述
输出一个整数,表示所有小于非负整数 n 的质数的数量
输入样例
10
输出样例
4
参考代码
#include
#include
using namespace std;
int main(){
int n;
cin>>n;
vector primes;
vector isPrime(n, 1);
for (int i = 2; i < n; ++i) {
if (isPrime[i]) {
primes.push_back(i);
}
for (int j = 0; j < primes.size() && i * primes[j] < n; ++j) {
isPrime[i * primes[j]] = 0;
if (i % primes[j] == 0) {
break;
}
}
}
cout< 02卡牌分组
问题描述
给定一副牌,每张牌上都写着一个整数。
此时,你需要选定一个数字 X,使我们可以将整副牌按下述规则分成 1 组或更多组:
- 每组都有
X张牌。 - 组内所有的牌上都写着相同的整数。
仅当你可选的 X >= 2 时返回 true。
1 <= deck.length <= 10^40 <= deck[i] < 10^4
输入描述
第一行输入一个整数表示 deck.length
第二行 deck.length 个由空格分割的整数代表 deck
输出描述
仅当你可选的 X >= 2 时返回 true ,否则返回 false
输入样例
8
1 2 3 4 4 3 2 1
输出样例
true
参考代码
#include
#include
using namespace std;
int gcd(int a, int b){
return b?gcd(b,a%b):a;
}
int main(){
int cnt[10000]={0};
int n;
cin>>n;
vector deck(n);
for(int i=0;i>deck[i];
cnt[deck[i]]++;
}
int g = -1;
for (int i = 0; i < 10000; ++i) {
if (cnt[i]) {
if (~g) {
g = gcd(g, cnt[i]);
} else {
g = cnt[i];
}
}
}
if(g >= 2){
cout<<"true";
}else{
cout<<"false";
}
return 0;
}
03元宵节
问题描述
小蓝家里有 n 种元宵馅, m 种元宵皮,每个元宵可以选择任意一种元宵馅和任意一种元宵皮。同时有 x 张桌子,每张桌子上放了 y 只碗,每只碗能放一只元宵。每只碗都要装一只元宵。小蓝 会告诉你 n、m、x、y 的值,想请问你有多少种装元宵的方式。答案对 z 取模。
-
两种方式被认为是不同的当且仅当至少有一只碗存在于两种方式的同一个位置但是里面有至少一个元宵不同。
-
两个元宵被认为是不同的当且仅当元宵馅不同或者元宵皮不同。
-
碗和桌子都是有编号的,但是你不能改变碗或桌子的编号。
-
你可以认为碗和桌子都是固定的,你只能改变元宵的种类和位置。
-
1 <= n、m <= 10^18 -
1 <= x、y <= 10^6 -
1 <= z < 10^9+7
输入描述
第一行输入五个整数分别表示 n、m、x、y、z
输出描述
输出一个整数
输入样例
1 2 1 3 998244353
输出样例
8
参考代码
#include
using namespace std;
#define ll long long
int main()
{
ll n,m,x,y,z;
cin>>n>>m>>x>>y>>z;
ll num1 = (n % z) * (m % z) % z;
ll num2 = x * y;
ll result = 1;
if (num2 == 0){
cout<<0;
} else {
while (num2){
if (num2 & 1){
result = (result * num1) % z;
}
num1 = (num1 * num1) % z;
num2 >>= 1;
}
cout< 04镜面反射
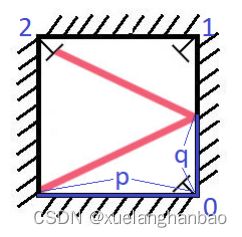
有一个特殊的正方形房间,每面墙上都有一面镜子。除西南角以外,每个角落都放有一个接受器,编号为 0, 1,以及 2。
正方形房间的墙壁长度为 p,一束激光从西南角射出,首先会与东墙相遇,入射点到接收器 0 的距离为 q 。
返回光线最先遇到的接收器的编号(保证光线最终会遇到一个接收器)。
示例1
1 <= q <= p <= 1000
输入描述
第一行输入两个整数分别表示 p、q
输出描述
输出最先遇到的接收器的编号
输入样例
2 1
输出样例
2
参考代码
#include
using namespace std;
int gcd(int a, int b){
return b?gcd(b,a%b):a;
}
int main(){
int p, q, result;
cin>>p>>q;
int g = gcd(p, q);
p /= g; p %= 2;
q /= g; q %= 2;
p == 1 ? result=0 : result=2;
if (p == 1 && q == 1) result = 1;
cout< 05判断一个点是否可以到达
给你一个无穷大的网格图。一开始你在 (1, 1) ,你需要通过有限步移动到达点 (targetX, targetY) 。
每一步 ,你可以从点 (x, y) 移动到以下点之一:
(x, y - x)(x - y, y)(2 * x, y)(x, 2 * y)
给你两个整数 targetX 和 targetY ,分别表示你最后需要到达点的 X 和 Y 坐标。如果你可以从 (1, 1) 出发到达这个点,请你返回 true ,否则返回 false 。
1 <= targetX, targetY <= 10^9
输入描述
第一行输入两个整数分别表示 targetX, targetY
输出描述
如果可以从 (1, 1) 出发到达这个点,请你返回 true ,否则返回 false
输入样例
6 9
输出样例
false
参考代码
#include
using namespace std;
int gcd(int a, int b){
return b?gcd(b,a%b):a;
}
int main(){
int x, y, result;
cin>>x>>y;
int g = gcd(x, y);
if(g&(g-1)==0){
cout<<"true";
}else{
cout<<"false";
}
return 0;
}
输入样例
6 9
输出样例
false
参考代码
#include
using namespace std;
int gcd(int a, int b){
return b?gcd(b,a%b):a;
}
int main(){
int x, y, result;
cin>>x>>y;
int g = gcd(x, y);
if(g&(g-1)==0){
cout<<"true";
}else{
cout<<"false";
}
return 0;
}