数字逻辑电路—第六章 时序逻辑电路

---

时序逻辑概述

##1、 组合逻辑电路&&时序逻辑电路
（1）组合逻辑电路：任何一个时刻，输入信号仅取决于当时的输入信号
（2）时序逻辑电路：不仅取决于当时的输入信号，还取决于电路原本的工作状态

2、时序逻辑电路的组成

（1）组合电路
组合电路最少一个输出必须反馈到存储电路的输入端
（2）存储电路—记忆以前的输入和输出
1）存储电路由触发器构成，也可以由带有反馈的组合电路构成
2）存储电路的状态至少有一个作为组合逻辑电路的输入，与其他输入信号共同决定电路的输出

x为输入信号，z为输出信号，y为状态信号，w为驱动信号

3、时序电路的分类

（1）同步时序逻辑电路
存储电路状态是靠时钟脉冲同步更新的
（2）异步时序逻辑电路
存储电路中，有的有时钟脉冲作用，有的没有时钟脉冲作用
即使在有时钟脉冲作用的存储电路中，存储器的更新也不是同步进行的
（3）米里型
输出信号不仅取决于存储电路的状态，而且取决于输入变量
（4）摩尔型
输入状态只取决于存储电路的状态，是米里型的一个特例

时序逻辑电路分析

1、时序逻辑电路分析步骤

（1）写出存储电路（触发器）的驱动方程
（2）写出存储电路的状态转移方程
（3）由状态转移方程/输出函数表达式，列出状态转移表/划出状态转移图
（4）画出工作波形（时序图）

寄存器、移位寄存器

1、数码寄存器

数码寄存器是能存放二进制数码的电路，由于触发器具有记忆功能，因而可以作为数码寄存器电路

2、移位寄存器

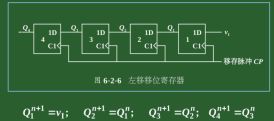
具有移位（左移、右移、双向）功能的寄存器

     M=0左移，M=1右移

移位寄存器的应用

（1）串行转并行

（2）并行转串行


Q5=1不影响，Q5^n+1=Q4+D15，与Q5无关

（3）脉冲节拍延迟
由于移位寄存器串行输入、串行输出时，输入信号经过n级移位寄存后才到输出端输出。因此输出信号延迟了n个移存脉冲才到达输出端输出，因此输出信号比输入信号延迟了n个移存脉冲的周期，这样就起到节拍延迟的作用。
（4）构成计数分频器、序列信号发生器

同步计数器

数字电路中使用最多的时序电路

1、作用：用来对时钟脉冲计数，也可以做定时、分频、执行数字运算
2、分类
（1）计数脉冲引入方式：同步计数器、异步计数器
（2）数字增减趋势：加法计数器、减法计数器、可逆计数器
（3）计数器数模值：二进制计数器、非二进制计数器

1、同步二进制计数器

状态转移方程：

2、二进制同步加/减计数器

1、M=1，进行加法计数，M=0，进行减法计数
2、M=0时，高位输入端的信号由低位触发器Q端引出；M-1时，高位输入信号由低位触发器~Q输入

3、二—十进制计数器

1、偏离状态：1010、1011、1100、1101、1110、1111，正常工作时不会出现，若计数器受到某种干扰，会错误地进入偏离状态
2、自启动性：偏离状态下自动转入有效序列的特性
3、输出信号Z是十进制计数器的进位信号，输出信号的周期恰好为输入计数脉冲CP周期的10倍，因此输入信号也可以视为输入计数脉冲CP的十分频信号，因而模10计数器也可以看成十分频器

4、集成同步计数器

（1）CT54161/CT74161（CT54160/CT74160） 【重点】

（背逻辑符号、功能表和引脚）

~CR端：清零端 ~LD：置数控制端（需要时钟，同步）
CTt、CTp使能端，高电平有效 CP：时钟 D3-D0：4位二进制输入
Q3-Q0：输出 Co：进位输出

计数功能：每来一个脉冲就计数一次，对于74LS161是0000-1111，十六进制，最后Co=1
74LS160是从0000-1001，是十进制计数器，最后Co进位

（2）十二位二进制加法计数器（ 74LS161）【重要】

~LD是置数端，CPD、CPu是使能端，均为1时执行计数功能
第一片接法就是16位计数
第二片CTp接Co，即第一片产生一个进位Co才计数一次
第三片与第二片的区别：第二片的Co接在第三片的CTp上，即第二片记满并且第一片记满，第三片才记一次

异步触发器

不同于同步计数器，时钟脉冲不一定都是计数输入脉冲，各级触发器的状态转移不是同一时钟作用下同时发生转移

1、4位二进制异步计数器（16分频）

    前一级的输出接后一级的时钟

状态转移方程：

（画工作波形会很直观）

从0000-1111
对电路图进行改变改变：如果将输入Qn变成~Qn，状态会从1111变到0000，实现十六进制减法
（4）最低位每来一个脉冲翻转一次，其他触发器在所有相邻最低位触发器由1->0时翻转一次
（5）特点
1）电路简单
2）工作速度慢，随着位数的增加，延时也大大增加

时延：Q1从1->0之后，Q2才能从1—>0……以此类推，需要等待，这就是时延，而且在改变的过程中，之前触发器的状态不能改变，否则会造成混乱，异步计数频率脉冲有非常严格的要求

采用中规模集成器件实现任意模值计数（分频）器

设计原理：从N进制（N

方法一：利用清除端复位法

对于分频比要求较大的情况下，应用更方便

到达最后一个状态时，利用最后一个状态产生一个清除信号，加到清除端，使计数器返回到S0状态，这样就跳跃了N-M个状态，从而实现了模值为M的计数分频

例1：4位二进制同步计数器（74LS161）实现模10分频

分析：在计数器的基础上增加判别和清零信号产生电路，当电路状态为1010时，产生清零信号，使计数器清零，回到0000状态

思考问题：

1、为什么选1010（1010是第11个状态），为什么会有11个状态呢？

因为161的清零是异步清零（不需要脉冲，只要满足~CR=0，那么Q3Q2Q1Q0=0000），所以只要探测到这个状态，就会立即清零，并不能维持一个时钟脉冲的时间，所以完整的时钟脉冲只是前面的10个脉冲，1010只是一瞬间，如果改成同步清零的话，因为采用同步时钟，是一整个脉冲信号，因此选择1001

2、基本触发器有什么作用

图中利用判别电路+基本触发器去产生清零信号，其中基本触发器可以忽略
（1）首先看看有没有触发器的区别

触发器11是保持状态，当没有触发器时，_{CR变得和Vo1一样长（没有图中那么长，因为清零信号只在一瞬间），当有触发器时，因为触发器的保持功能，}CR能维持一个脉冲宽度的宽度。
（2）那为什么需要保持一个脉冲宽度呢？
因为如果集成器件各触发器翻转过程中，由于速度不等，就可能不能使全部触发器置0，采用触发器之后，Q端的清零信号宽度和计数脉冲CP=1的持续时间相等，可确保计数器可靠清零
（3）有没有必要加入触发器呢？
一般来说是没有必要加入触发器的，将Vo1直接加到计数器清零端是可以实现清零的，上述现象出现的概率很少

方法二：利用置入控制端的置位法

采用中规模集成器件的置入控制端，以置入某一固定二进制数值的方法，从而使N进制计数跳跃（N-M）个状态，实现模值为M的计数分频
例 用4位二进制同步计数器74161（16个状态），实现模10数分频

_{LD是置位端，跳过0000-0101的6个状态，从0110到1111共10个状态，到最后一个状态会产生进位Co标志，因此令}LD=~Co实现“跳”到0110，采用同步置数，1111状态是能维持1个脉冲周期的时间的。
电路是固定结构，如果需要改变模值M，只需要改变输入端D3-D0的输入数据2^n-m的二进制代码

例2：应用4位二进制同步计数器CT54161，实现模12计数分频，要求计数器从0000开始计数

（解法1）

当在0000时，“跳”到0101开始，到1111刚好12个状态，因此采用电路Q0+Q1+Q2+Q3，在四位均为0000的时候才会输出0，启动置数

例2—— 置数输出方波信号

（解法2）
方波信号就是对称信号，将16位信号分成两半，每一半对称地跳过两个信号总线，根据观察，最高位D3 总是和输出的最高位相同，所以直接将Q3连到D3处，低3位和解法1思路一样

用集成移位寄存器实现任意模值M的计数分频

移位寄存器的状态转移是按照移存规律进行的，因此构成任意模值技术分频器的状态转移必然符合一寸规律，一般称为移存型计数器。常用的移存型计数器有环形计数器和扭环计数器

1、环形计数器的构成

先回顾下74195的功能
（1）~CR=0是，是清除功能，Q3-Q0=0000
（2）SH/~LD=0，是置数功能，Q3-Q0=D3-D0
（3）SH/~LD=1，是移位功能，Q0->Q1->Q2->Q3，每来一个脉冲就移一位
（4）在移位状态下，CP=0，是保持功能
再看看启动脉冲，只有一个简单低电平，短时间的低电平是为了将0111置入到芯片中，置完就维持高电平不变，执行移位功能
Q0是如何移位的呢？根据JK触发器的状态方程可以算出Q0^n+1=Q3，（即Q3是Q0的下一个状态）
所以移位步骤如下：
Q0->Q1->Q2->Q3->Q0

是一个模4计数器

2、扭环形计数器

与环形计数器的区别是：环形计数器通过Q3端送到JK端，而扭环形计数器是通过~Q3端送到JK端
根据真值表可以发现，环形计数器是模4计数器，而扭环形计数器是模8计数器
不管上面放什么数，甚至是不接（1111），也是模8计数器