智能优化及其应用——课程实验（粒子群算法）

---

前言

  这学期的智能优化课程主要介绍了人工智能领域内的一些优化算法，课程实验要求编程实现任意一种算法解决优化问题。个人对粒子群算法比较感兴趣，主要查阅了《智能优化算法及其MATLAB实例（第3版）》（作者：包子阳,余继周,杨杉）一书，学习了粒子群算法这一章，并且参考书上的matlab实例，采用python进行编程实现。

---

以下内容主要是本人对课程实验的记录，如果有错误或不妥之处，望指正。
另：点击此处可查看完整代码进行测试

一、粒子群算法原理

  一群鸟在区域中随机搜索食物，每只鸟知道自己当前位置离食物多远（即当前搜索结果），在搜索过程中，每只鸟会记住自己曾经离食物最近的位置（即历史最优搜索结果）并向该位置附近搜索；同时每只鸟通过交流获得其他鸟的位置与搜索结果，然后鸟群就会向目前离食物最近的鸟（即全局最优搜索结果）附近搜索，直至搜索到食物（即最优值）及其位置（即最优解）。
  粒子群算法模仿这种鸟类捕食行为，将优化问题的搜索空间类比于鸟类的飞行空间，将每只鸟抽象为一个粒子，粒子只有位置和速度两个属性，用自身位置表征问题的一个解，粒子在当前位置的搜索结果即当前解对应与问题的值，粒子以一定的速度更新位置进行搜索，并且其速度受到群体中其他粒子位置和历史最佳位置的影响进行更新。每个粒子不停地迭代更新直至搜索到最优值和最优位置

二、粒子群算法建模

  在D维的目标搜索空间中， 随机初始化N个粒子组成一个群落，其中第i个粒子的位置表示为一个D维的向量，记为
$$X_i=(x_{i1},x_{i2},\cdots ,x_{iD}),i=1,2,\cdots ,N$$第i个粒子的“飞行”速度也是一个D维的向量，记为
$$V_i=(v_{i1},v_{i2},\cdots ,v_{iD}),i=1,2,\cdots ,N$$由优化函数计算每个粒子的适应度值，记为
$$F_i=fit(X_i),i=1,2,\cdots ,N$$然后开始迭代搜索，第i个粒子迄今为止搜索到的最优位置称为个体极值，记为
$$P_{Best}=(p_{i1},p_{i2},\cdots ,p_{iD}),i=1,2,\cdots ,N$$整个粒子群迄今为止搜索到的最优位置为全局极值，记为
$$G_{Best}=(g_{i1},g_{i2},\cdots ,g_{iD}),i=1,2,\cdots ,N$$每次迭代中粒子找到这两个位置后，根据以下两个式子来更新自己的速度和位置：
$$v_{ij}(t+1)=w{v}_{ij}(t)+c_1{r}_1(t)[p_{ij}(t)-x_{ij}(t)]+c_2{r}_2(t)[g_{ij}(t)-x_{ij}(t)]$$$$x_{ij}(t+1)=x_{ij}(t+1)+v_{ij}(t+1),i=1,2,\cdots ,N$$$$i=1,2,\cdots ,N;j=1,2,\cdots ,D$$其中$w$为惯性系数，$c_1$和$c_2$为学习因子，也称加速常数；$r_1$和$r_2$为［0，1］范围内的均匀随机数，增加了粒子飞行的随机性。速度更新公式由三部分组成：第一部分为“惯性”部分，反映了粒子的运动“习惯”，代表粒子有维持自己先前速度的趋势；第二部分为“认知”部分，反映了粒子对自身历史经验的记忆或回忆，代表粒子有向自身历史最佳位置逼近的趋势；第三部分为“社会”部分，反映了粒子间协同合作与知识共享的群体历史经验，代表粒子有向群体历史最佳位置逼近的趋势。

三、Python编程实现

0.优化问题

  选取《智能优化算法及其MATLAB实例（第3版）》中的三个优化问题实例：

• 计算$f(x)=x+6\sin (4x)+9\cos (5x),x\in [0,9]$的最小值
• 计算$f(x,y)=3cos(xy)+x+y^2,x,y\in [-4,4]$的最小值
• 计算$f(x)={\sum }_{i=1}^{10}{x}_i^2,x_i\in [-20,20]$的最小值

1.定义PSO类

  给定相关参数，实例化一个PSO类，初始化生成粒子群，粒子的初始位置和速度的每一维均为给定范围内的随机数，根据适应度函数计算每个粒子的适应度值，初始时每个粒子的局部最优位置均为自身，全局最优位置为所有粒子中适应度最优的粒子的位置。

class PSO:
    def __init__(self,size,dimension,time,x_bound,v_bound,c1,c2,w):
        self.size = size                #种群大小
        self.dimension = dimension      #粒子维数
        self.time = time                #迭代次数
        self.c1 = c1                    #加速常数1
        self.c2 = c2                    #加速常数2
        self.w = w                      #惯性权重
        self.x_bound = x_bound          #位置的范围
        self.v_bound = v_bound			#速度的范围
        self.x = np.random.rand(self.size,self.dimension) * (x_bound[1] - x_bound[0]) + x_bound[0]   #位置初始化
        self.v = np.random.rand(self.size,self.dimension) * (v_bound[1] - v_bound[0]) + v_bound[0]   #速度初始化
        self.p = self.x.copy()           #局部最优位置
        self.pbest = self.fit()          #局部最优结果
        self.gbest = min(self.pbest)     #全局最优结果
        self.g = self.p[self.pbest.index(self.gbest)].copy()   #全局最优位置
        self.gbestlist = []      #记录每一代的全局最优结果

2.定义适应度函数

  根据优化函数计算粒子群x中每个粒子i对应的适应度值一起返回为f，循环中三行代码分别为本次实验的三个优化函数，也可以自行定义其他的优化函数使用。

    def fit(self):
        f = []
        for i in self.x:
            f.append(i[0]+6*math.sin(4*i[0])+9*math.cos(5*i[0]))
            # f.append(3 * math.cos(i[0] * i[1]) + i[0] + i[1] * i[1])
            # f.append(sum(np.power(i,2)))
        return f

3.定义迭代运行函数

  每次迭代过程中，计算粒子的适应度值，更新全局最优和局部最优。再根据全局最优和局部最优位置更新速度和位置，同时进行速度和位置的边界约束。
、

    def run(self):
        for i in range(self.time):
            f = self.fit()   #计算粒子群的适应度
            for j in range(self.size):
                if f[j]<self.pbest[j]:    #更新局部最优值和最优位置
                    self.pbest[j] = f[j]
                    self.p[j] = self.x[j].copy()
                    if f[j] < self.gbest:   #更新全局最优值和最优位置
                        self.gbest = f[j]
                        self.g = self.x[j].copy()
                self.v[j] = self.w * self.v[j] + self.c1 * np.random.rand() * \
                            (self.p[j]-self.x[j]) + self.c2 * np.random.rand() * (self.g-self.x[j])   #更新粒子群的速度
                for k in range(self.dimension):   #速度大小约束
                    if(self.v[j][k] > self.v_bound[1] or self.v[j][k] < self.v_bound[0]):
                        self.v[j][k] = np.random.rand() * (v_bound[1] - v_bound[0]) + v_bound[0]
                self.x[j] = self.x[j] + self.v[j]   #更新粒子群的位置
                for k in range(self.dimension):     #位置大小约束
                    if(self.x[j][k] > self.x_bound[1] or self.x[j][k] < self.x_bound[0]):
                        self.x[j][k] = np.random.rand() * (x_bound[1] - x_bound[0]) + x_bound[0]
            self.gbestlist.append(self.gbest)       #保存每一代的全局最优值

4.定义结果输出函数

  迭代结束后输出适应度进化曲线和最优结果。

    def result(self):
        plt.figure()
        plt.plot(range(self.time), self.gbestlist, color='red', marker='.', ms=1.5)
        plt.rcParams['axes.unicode_minus'] = False
        plt.margins(0)
        plt.xlabel(u"迭代次数")  # X轴标签
        plt.ylabel(u"适应度")  # Y轴标签
        plt.title(u"迭代过程")  # 标题
        plt.show()
        print('最优解为:',end='')
        print(self.g)
        print('最优值为%f'%self.gbest)

5.编写main函数

  给定对应优化问题的相关参数，一般定义w=0.8，c1=c2=1.5，x,v的范围由问题决定，size，dimension，time根据运行结果调整（此处代码中的三段参数分别对应三个优化问题，与2中的适应度函数对应，测试不同优化问题时，修改注释即可），然后实例化PSO对象，运行run()函数实现粒子群算法的迭代搜索，最后输出适应度曲线。

if __name__ == '__main__':
    size = 10
    dimension = 1
    time = 50
    x_bound = [0, 9]
    v_bound = [-3, 3]
    c1 = 1.5
    c2 = 1.5
    w = 0.8

    # size = 100
    # dimension = 2
    # time = 200
    # x_bound = [-4, 4]
    # v_bound = [-1, 1]
    # c1 = 1.5
    # c2 = 1.5
    # w = 0.8
    
    # size = 100
    # dimension = 10
    # time = 200
    # x_bound = [-20,20]
    # v_bound = [-10,10]
    # c1 = 1.5
    # c2 = 1.5
    # w = 0.8

    pso = PSO(size,dimension,time,x_bound,v_bound,c1,c2,w)
    pso.run()
    pso.result()

6.结果展示

（1）计算$f(x)=x+6\sin (4x)+9\cos (5x),x\in [0,9]$的最小值
运行结果:

可作该一元函数的曲线图知，粒子群算法在众多局部最优值中找到了全局最优值

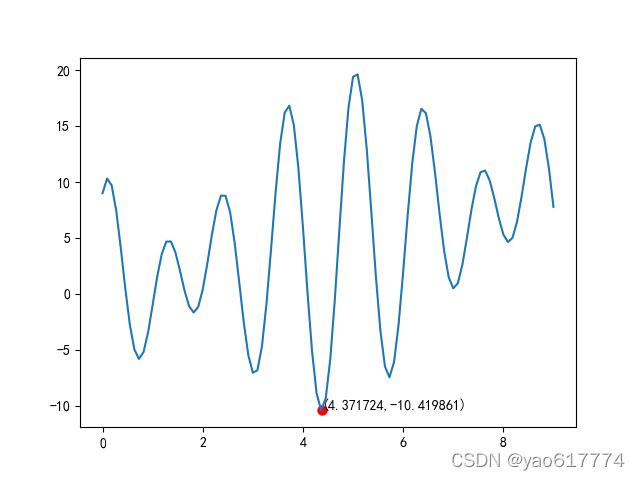
适应度曲线图：

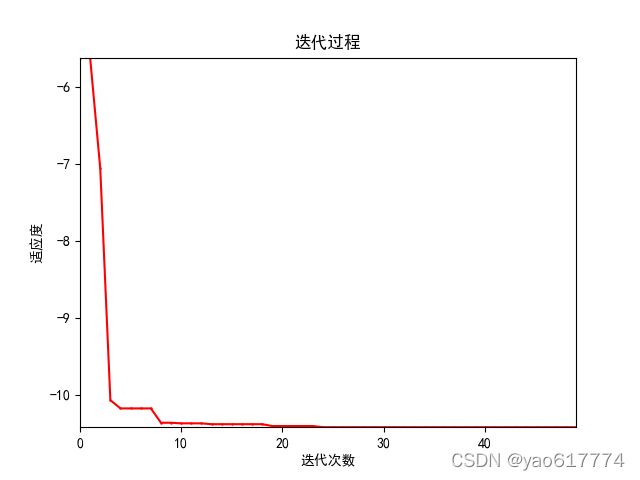
（2）计算$f(x,y)=3cos(xy)+x+y^2,x,y\in [-4,4]$的最小值
运行结果:

适应度曲线图：

（3）计算$f(x)={\sum }_{i=1}^{10}{x}_i^2,x_i\in [-20,20]$的最小值
运行结果:适应度曲线图：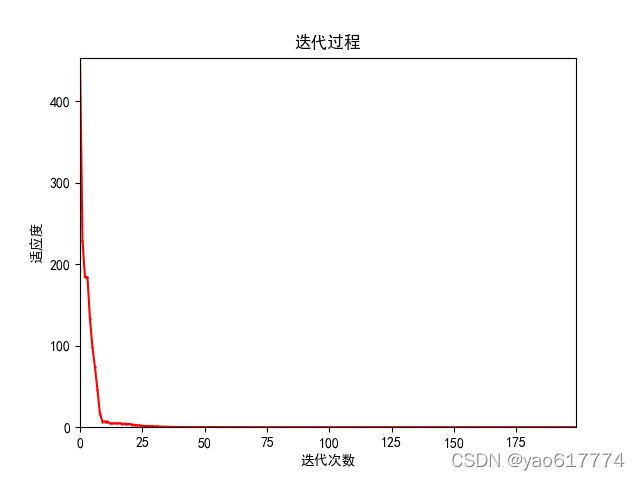

---

总结

  本次实验主要时通过学习粒子群算法原理，了解粒子群算法的基本流程，掌握粒子群算法的算法建模，编程解决优化问题。在实验中，分别解决了一个1维，2维，多维优化函数最小值求解问题。除此之外，上诉代码也提供了一个基础的解决连续型优化问题的框架，修改适应度函数，提供对应的参数，即可测试其他的优化问题。
  另外，本文对于粒子群算法原理的讲解以及实际的应用比较浅显，如果想更详细地了解粒子群算法（包括参数调节，离散问题，算法改进等），可以参考《智能优化算法及其MATLAB实例（第3版）》一书和这篇讲解比较完整的博客