解析树构建器以及相关计算

#数据结构与算法分析#

#慕课学习#

二叉树的应用：

解析树：可以解析现实生活中的自然语言，人工创键的语言：机器语言等等。今天来学习使用解析树来解析数学表达式。

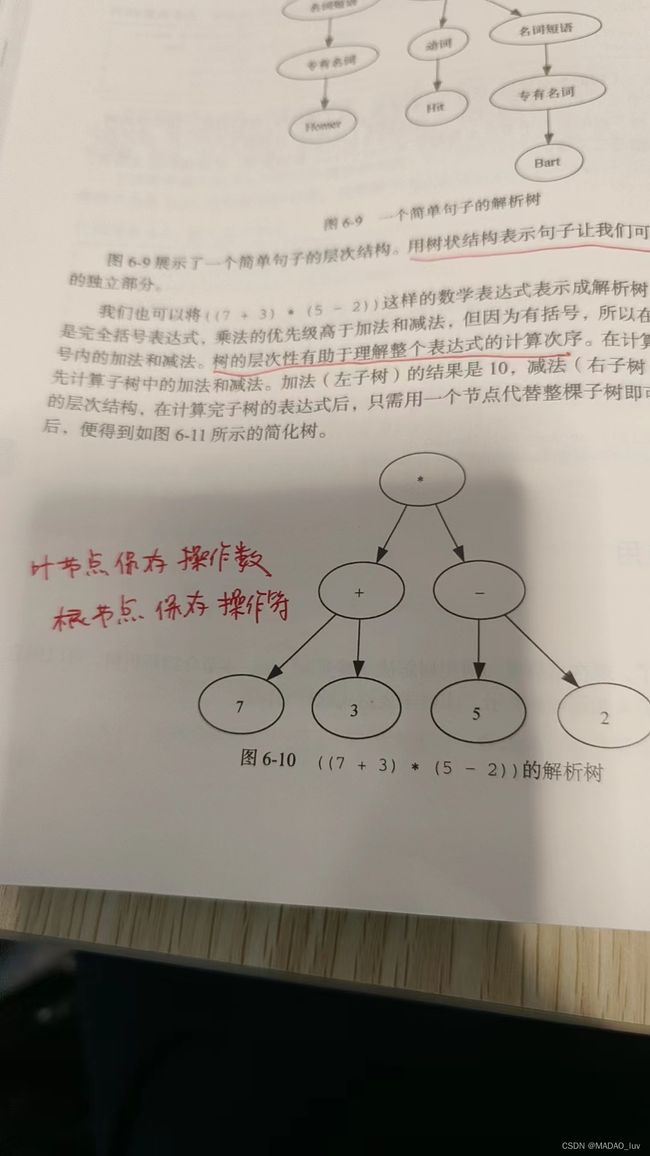
让我们看看一个简单的数学表达式层次的结构。

如下图所示。

我们用子节点保存操作数，而用根节点保存操作符。

一.解析树的重点

1.如何根据完全括号表达式构建解析式

2.如何计算解析树中的表达式

3.如何将解析树还原成最初的数学表达式

构建解析树的第一步式将表达式字符串拆分成标记列表。需要考虑4种标记：左括号，右括号，运算符和操作树。在我们的认识中，左括号代表新表达式的起点，那么右括号便是表达式的终点，，那么当遇到左括号时，创建一颗对应表达式的新树。反之，遇到右括号则意味着到达该表达式的终点。操作数即是叶子节点，也是其运算符的子节点。  每一个运算符都有左右节点 因为进行一次运算需要一个操作符和两个操作数。

二.实现解析树

我们便可以定义以下4条规则：

1.当前标记为（，就为当前节点添加一个左子节点，并下沉至该子节点。

2.当前标记在列表['+', '-', '/', '*']中，就将当前节点的值设为当前标记对应的运算符；为当前节点添加一个右子节点，并下沉至该子节点。

3.当前标记为数字时，就将当前节点的值设为这个数并返回至父节点；

4.当前标记为 ），就跳到当前节点的父节点。

那么我们开始吧。

#记住要创建BInaryTree 和 Stack这个数据结构。
 
def buildParseTree(fpexp):
    fplist = fpexp.split()#将要解析的数学表达式分解为字符
    pStack = Stack() #创建一个栈
    eTree = BinaryTree() #创建一个空树
    pStack.push(eTree) 
    currentTree = eTree  

在这里有四个变量

1.fplist 是被一个装有一个个表达式字符的列表

2.pStack 是用来暂存节点的，因为父节点可以访问子节点，但是无法返回父节点，那么就使用栈来暂存节点，已达到规制2，4

3.eTree是创建一个空树，用来存放操作数和操作符

4.currentTree 表示当前的节点

那么我们接下来继续看。

    for i in fplist:
        if i == '(':
            currentTree.insertLeft('')
            pStack.push(currentTree)
            currentTree = currentTree.getLeftChild
#插入左节点为空的，并将原先的父节点压入栈中，当前节点为左子节点
        elif i not in '+-*/)':
            currentTree.setRootVal(i)
            parent = eStack.pop()
            currentTree = parent
#为数字，将数字存入该节点，并返回到父节点
         elif i in '+-*/':
             currentTree.setRootVal(i)
             currentTree.insertRight('')
             eStack.push(currentTree)
             currentTree = currentTree.getRightChild
#当为操作符的时候，把操作符存入当前的节点，并创建新节点，自动降级
         elif i == ')':
              currentTree = eStack.pop()
#当为')'时，返回到父节点
         else:
              raise ValueError("Unkown Operator")
      return eTree

最后返回循环后的树结构。

最后一个else语句是为了防止遇到一些其他的符号出现，就抛出一个ValueError异常

那么，有了一棵解析树之后，我们能干嘛捏？？？？

我们的目的还不是要去计算出来我们想要的值。

那

三.计算解析树

根据解析树是一个递归的数据结构，那么我们也可以使用递归来简化计算。

它的基本结束情况是咩？？？ 很自然的就是，只有它一个节点，而且没有其他子节点。

这个节点不就是叶节点吗。

1.基本结束条件就是----叶节点

那么，我们还要想想怎么向这个基本条件靠近呢？

这时，BinaryTree类中有方法来达到目的

def getLeftChild(self):
    return self.leftchild

def getRightChild(self):
    return self.rightChild

那么，我们就开始，实现这个操作吧。

import operator
def evaLuate(parseTree):
    opers = {'+':operator.add, '-':operator.sub,
             '*':operator.mul, '/':operator.truediv}
#使用字典，在计算时便可以直接引用值
    LeftC = paresTree.getLeftChild()
    RightC = paresTree.getRightChild()
    
    if LeftC and RightC:
        fn = opers[parseTree.getRootVal]
        return fn(evaLuate(Leftc),evaLuate(RightC)]
    else:
        return paresTree.getRootVal()

首先，获取指向当前节点的左右子节点的引用。如果左右子节点的值都是None，就说明当前节点确实是叶子节点。

如果当前子节点不是叶子节点，则查看当前节点中储存的运算符，并将其应用于左右子节点的递归计算结果。

这个便是解析树的计算了，感谢各位的观看。谢谢，若要任何疑问，欢迎来到评论区留下你的疑问