Crypto基础之密码学

FLAG：20岁的年纪不该困在爱与不爱里，对吗
专研方向: 密码学，Crypto
每日emo：今年你失去了什么？

---

---

前言

浅谈密码学：

密码学可以分为古典密码学和现代密码学，两者有什么区别呢
密码学研究：怎么让密码这个数据不泄露，不被破译。

古典密码学：我们想要发送的信息，不想要第三方知道，对这个信息进行加密。

现代密码学：除了研究密码信息的保密问题，还要考虑其他很多方面的安全隐患，比如窃听、篡改、伪装、否认。

---

一、编码

编码是信息表达另一种表达方式，掌握各类编码转化技巧是密码学的基础。
编码 (encode)和解码 (decode)是个相当广泛的话题，涉及计算机对信息处理的根本方式。最常用的编码是ASCII（美国信息交换标准代码），包含国际通用的大小写字母、数字、常见符号等，是互联网的通用语言。

---

Base编码

base64：

base64 是一种基于 64 个可打印字符来表示二进制数据的表示方法。由于 2⁶ = 64 ，所以每 6 个比特为一个单元，对应某个可打印字符。3 个字节有 24 个比特，对应于 4 个 base64 单元，即 3 个字节可由 4 个可打印字符来表示。相应的转换过程如下图所示：

在 base64 转换的时候，3 字节的数据先后放入一个 24 位的缓冲区中，先来的字节占高位 。数据不足3字节，缓冲器中剩下的位用0补足。每次取出 6bit，按照其值选择中的字符作为编码后的输出，直到全部输入数据转换完成。若原数据长度不是 3 的倍数且剩下1个输入数据，则在编码结果后加 2 个 “ = ”，若剩下 2 个输入数据，则在编码结果后加 1 个 “=”。所以，识别 Base64 编码的一种方法是看末尾是否有 “ = ” 。但是这种识别方法并不是万能的，当编码的字符长度刚好是3的倍数时，编码后的字符串末尾不会出现 “=”

ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/

---

Base32 和 Base16：

Base 系列中还有 Base32 和 Base16 ，其实 Base32 / Base16 与 Base64 的目的一样，只是具体的编码规则不同。Base32 编码将二进制文件转换成 32 个 ASCII 字符组成的文本，转换表为

ABCDEFGHIJKLMNOPQRSTUVWXYZ234567

Base16 编码则将二进制文件转换成由 16 个字符组成的文本，这 16 个字符为 0~9和 A~F，其实就是 Hex 编码。

---

uuencode：

uuencode 衍生自 “unix-to-unix encoding” ，曾是 UNIX 系统下将二进制的资料借由 UUCP 邮件系统传输的一个编码程式，是一种二进制到文字的编码。uuencode 将输入字符以每3字节为单位进行编码，如此重复。如果最后剩下的字符少于 3 字节，不足部分用 0 补齐。与 Base64 一样， uuencode 将这 3 字节分为4组，每组以十进制数表示，这时出现的数字为 0~63 。此时将每个数加上 32，产生的结果刚好落在 ASCI 可打印字符的范围内。经过 uuencode 编码过后的字符，可以看到 uuencode 的特征: 特殊符号很多.

---

xxencode：

xxencode 与 Base64 类似，只不过使用的转换表不同：、

+-0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz

只是多了“ - ”字符，少了“ / ”字符，而且 xxencode 末尾使用的补全符号为“ + ”，不同于Base64 使用的“ = ”.

---

URL编码

URL编码又称为 百分号编码。如果一个保留字符在特定上下文中具有特殊含义，且URI中必须使用该字符用于其他目的，那么该字符必须进行编码。URL编码一个保留字符，需要先把该字符的ASCII编码表示为两个十六进制的数字，然后在其前面放置转义字符“ % ”，置入URI中的相应位置（非ASCI字符需要转换为 UTF-8 字节序，然后每字节按照上述方式表示）。例如，如果“ / ”用于URI的路径成分的分界符，则是具有特殊含义的保留字符。如果该字符需要出现在URI一个路径成分的内部，，则应该用“ %2F ”或“ %2f ”来代替“ / ".

二、古典编码

移位密码

密码和编码都是加密，但是有着本质区别：那个密码比编码多一个密钥（key）。我们将数据（明文）通过一定规则（秘钥）进行打乱混编（加密）得到字符串（密文），这就是密码的基本流程。密码学中，一般将明文用m表示，将密文用c表示，将秘钥k表示。

简单移位密码

有一个明文“qianxinshequ”，有一个秘钥“4132”，用下面的形式进行书写：

m="qianxinshequ"
k="4132"

当m为qianxinshequ的时候，先按照秘钥长度对其进行分割，已知 len(k)=4 ：

qian xins hequ

m被分为了3部分，按照k的数字顺序对每一部分的明文进行移位加密。根据k，每一部分的明文第一位被换到了第四位，第二位被换到了第一位，第三位依旧是第三位，第四位被换到第二位。剩下的两部分，以此类推。

经过变化，m变为：

inaq isnx euqh

合并就变成了密文：

inaqisnxeuqh

一个简单移位密码完成。

云影密码

云影密码仅包含01248数字，其中0用于分隔，其余数字用于做加和操作之后转换为明文。

例如：

m = "QIANXIN"

加密之后就是

c = "88108101084208880810842"

解密是这样的

881 81 1 842 888 81 842

各组相加

17 9 1 14 24 9 14

对应

Q I A N X I N

连起来就是m

m = "QIANXIN"

加密程序:

def yunying_decode(c):
    t="abcdefghijklmnopqrstuvwxyz"
    l=c.split("0")
    r=""
    for i in l:
        tep=0
        for j in i:
            tep+=int(j)
        r+=t[tep-1]
    return r

if __name__ =="__main__":
    print yunying_decode("8842101220480224404014224202480122")

---

栅栏密码

栅栏密码是一种规则比较特殊的移位密码，他的k是一个数字，用来表示栅栏的长度。其具体加密过程为，将要加密的m分成若干组。每组一共有k个字符。然后取每组第一个字符顺次连接，组成第一个字符串。然后再将第二个字符顺次连接，组成第二个字符串。以此类推，直到所有的m加密完毕。最后将加密后的字符串拼接在一起，便是c

例：

m = "qianxin"
k = "2"

按照k进行分解

qi an xi n

每组首位相加，以此类推

qaxn ini

合并得出c

c = "qaxnini"

---

曲路密码

将m填入一个表中，按照定向的连贯的顺序进行遍历，对其进行加密，是移位密码的一种。

此时，k看起来是一个表的形式，但仍然可以用字符串进行表达。因为k就是行列数。如下图所示：修改行列数就可以修改k。

有以下m

m = "qianxinyuanchuang"

k为7行5列，c为：

unihcxnngaaiunayq

---

替代密码

什么是代替密码?
首先构造一个或多个密文字母表，然后用密文字母表中的字母或字母组来代替明文字母或字母组，各字母或字母组的相对位置不变，但其自身发生改变。

代替密码又分为单表代替密码、多表代替密码和多名代替密码。

单表代替密码：
单表代替密码又称简单代替密码，它只使用一个密文字母表，并且由密文字母表中的一个字母代替明文字母表中的一个字母。
所以说单表代替建立了由密文到明文的一对一的映射关系。

多表代替密码：
由于单表代替密码只是用一个密文字母表，很容易破解。提高密码强度的一个方法是采用多个密文字母表。
最典型的多表代替密码是Vigenre密码。
维吉尼亚密码使用26个密文字母表，将26个密文字母表排在一起成为Vigenre方阵，如下图所示：

维吉尼亚密码的规则是用明文字母在方阵中的列和密钥字母在方阵中的行的交点处的字母来代替该明文字母。例如，明文字母为p，密钥字母为y，就用交点处的n来代替字母p。
维吉尼亚密码的解密就是利用维吉尼亚方阵进行反替换。例如，密文J,密钥是X，首先根据密钥J找到密文字母表，再查找密文X所在的列，该列与明文字母表的交点就是对应的明文O

多名代替密码：
为了抵抗频率分析攻击，希望密文中不残留明文字母的频率痕迹。一种明显的方法是设法将密文字母的频率分布拉平。

---

恺撒密码

单表替代密码,通过将字母一定的位数来实现加密和解密,移动的位数称为偏移量.
所以位数就是恺撒密码的密钥,只考虑可见字符,并且都为ascii码,所以128为模数.

加密：

def caser_encode(m,k):
    c=""
    for i in m:
        c+= chr((ord(i)+k)%128)
    return c

print caser_encode("flag{kaisamima}",3)

解密：

def caser_decode(c,k):
    m=""
    for i in c:
        m+= chr((ord(i)-k)%128)
    return m

print caser_decode("iodj~ndlvdplpd\x00",3)

ROT13:
在恺撒密码中,有一个特例,当k=13,只作用于大小写英文字母的时候称为ROT13,准确地来说它是一种编码,是ctf的常客.
通常会作用于md5, flag等字符串上,而我们都知道,md5字符只有ABCDEF,对应的ROT13为NOPQRS,flag对应的是SYNT

---

培根密码:

培根密码一般使用两种不同的字体表示密文,关键是字体,使用AB代表两种字体,5个一组表示密文

---

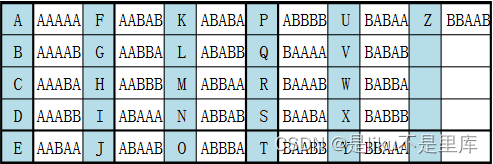
仿射密码

仿射密码是加法密码和乘法密码的结合，映射函数为：

其中，要求（k1，n）= 1，0≤k0

---

现代密码

分组密码和序列密码:

---

分组加密：

分组加密(Block Cipher) 又称为分块加密或块密码，是一种对称密码算法，这类算法将明文分成多个等长的块 (Block) ，使用确定的算法和对称密钥对每组分别加密或解密。分组加密是极其重要的加密体制，如DES和AES曾作为美国政府核定的标准加密算法，应用领域从电子邮件加密到银行交易转账，非常广泛。
本质上，块加密可以理解为一种特殊的替代密码，只不过每次替代的是一大块。因为明文空间非常巨大，所以对于不同的密钥，无法制作一个对应明密文的密码表，只能用特定的解密算法来还原明文。

序列密码：

通俗讲，序列密码就是利用初始密钥（种子密钥），产生密钥流，再利用密钥流，对明文逐比特进行加密（异或运算），解密相同，将密文与密钥进行逐比特异或运算。
由于密钥流的周期性会导致加密的不安全，但是非周期（随机）又存在协商难题，因此序列密码在产生密钥流时采用的是伪随机数（周期很大的周期序列）
采用伪随机数近乎完美地解决了以上两个难题，也实现了一次一密的加密方案。
序列密码又分为同步序列密码与自同步序列密码
1）同步序列：密文只与明文和密钥有关，密文不参与加密。
2）自同步序列：密文参与加密，密文不仅与明文和密钥有关，还与之前的密文有关。

---

公钥密码

公钥密码 (Public Key Cryptography)，又称为非对称密码，其最大特征是加密和解密不再使用相同的密钥，而使用不同的密钥。使用者会将一个密钥公开，而将另一个密钥私人持有，这时这两个密钥被称为公钥和私钥。一般来说，公钥和私钥是难以互相计算的，但它们可以互相分别作为加密密明和解密密钥。当信息发送者选择采用接收者的公钥加密时，接收者收到信息后使用自己的私钥解密，这样便可保持信息的机密性；若信息发送者使用自己的私钥对信息摘要进行加密，接收者使用发送者的公钥对摘要进行验证，即可起到签名的作用，可以保证信息的认证性和不可否认性。

RSA是一种公钥密码算法，它的名字由三位开发者，即Ron Rivest、Adi Shamir和Leonard Adleman的姓氏的首字母组成的。 RSA被用于公钥密码和数字签名。

公钥加密系统
在一个公钥加密系统中，任何人参与者都拥有独自的公钥和密钥，通常用P表示公钥，用S表示密钥，公钥用于加密，密钥用于解密。并且公钥可以公开，任何人都可以使用这个公钥发送一段密文，而只有私钥的持有者才可以用私钥解密

公钥和私钥对应的函数互为反函数

RSA公钥加密体系基于一个数论事实：把两个大质数相乘很容易，但是分解大数为两个质数的乘积很难

RSA加密
在RSA公钥加密系统中，可以通过以下过程创建一对公钥和私钥

1.任意选取远大于信息 M 的大质数 p 和 q，且 p != q
2.令 n = pq
3.计算 φ = (p-1)(q-1)
4.选取一个与 φ 互质的小奇数 e
5.计算对模 φ 意义下的 e 的乘法逆元 d，即 ed ≡ 1 (mod φ)
6.公开 P=(e, n)，此即为RSA公钥
7.隐藏 S=(d, n)，此即为RSA私钥

对于明文 M，使用以下函数进行加密

对于密文 C，使用以下函数进行解密