【独家OD2023C卷真题】20天拿下华为OD笔试【DFS】2023C-计算三叉搜索树的高度【欧弟算法】全网注释最详细分类最全的华为OD真题题解

题目描述与示例

题目描述：

定义构造三叉搜索树规则如下：

每个节点都存有一个数，当插入一个新的数时，从根节点向下寻找，直到找到一个合适的空节点插入。

查找的规则是：

1. 如果数小于节点的数减去 500，则将数插入节点的左子树
2. 如果数大于节点的数加上 500，则将数插入节点的右子树
3. 否则，将数插入节点的中子树

给你一系列数，请按以上规则，按顺序将数插入树中，构建出一棵三叉搜索树，最后输出树的高度。

输入描述

第一行为一个数 N，表示有 N 个数，1 <= N <= 10000

第二行为 N 个空格分隔的整数，每个数的范围为[1, 10000]

输出描述

输出树的高度(根节点的高度为 1)

示例一

输入

5
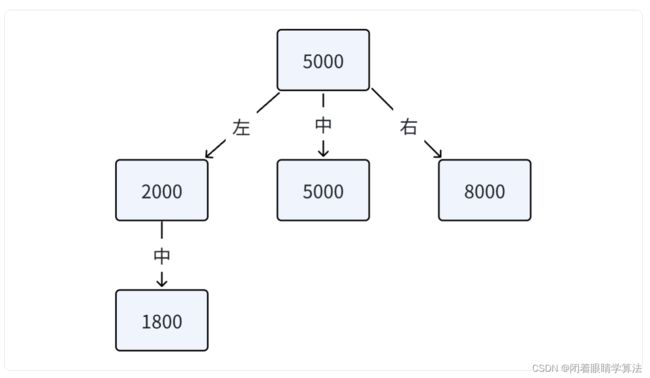
5000 2000 5000 8000 1800

输出

3

说明

最终构造出的树如下，高度为 3：

示例二

输入

3
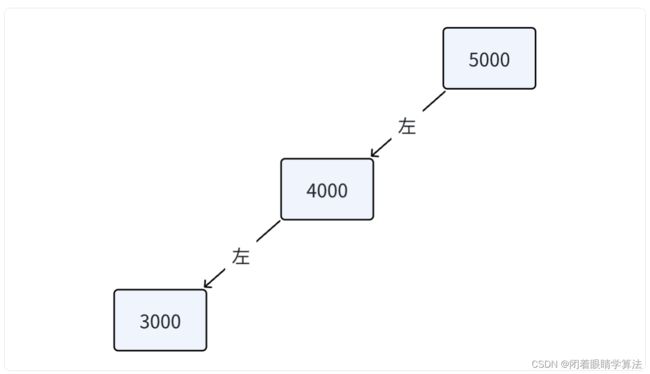
5000 4000 3000

输出

3

说明

最终构造出的树如下，高度为 3：

示例三

输入

9
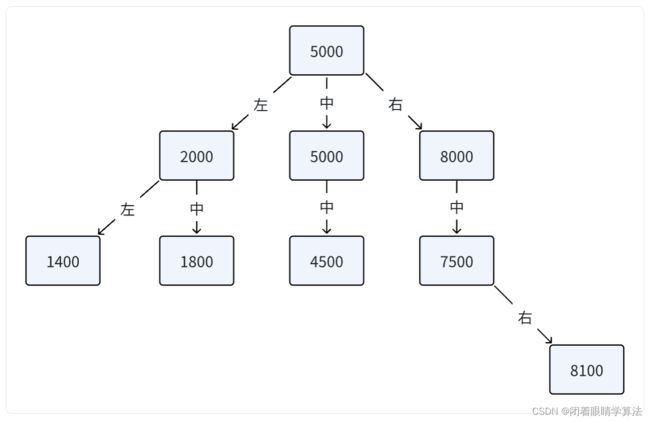
5000 2000 5000 8000 1800 7500 4500 1400 8100 

输出

4

说明

最终构造出的树如下，高度为 4：

解题思路

这道题题面不长，但对于没有接触过搜索树的概念的同学来说，可能是比较费解的。

节点的表示

本题的节点最好通过构建节点类class Node来表示。之所以使用节点类而非邻接表，是因为邻接表要求节点的值是唯一的。但在示例中显然节点的值不唯一，因此使用邻接表来建树并不方便。三叉树的节点类可以用如下代码表示：

# 构建树节点类
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.mid  = None
        self.right = None

三叉搜索树的节点插入过程（举例说明）

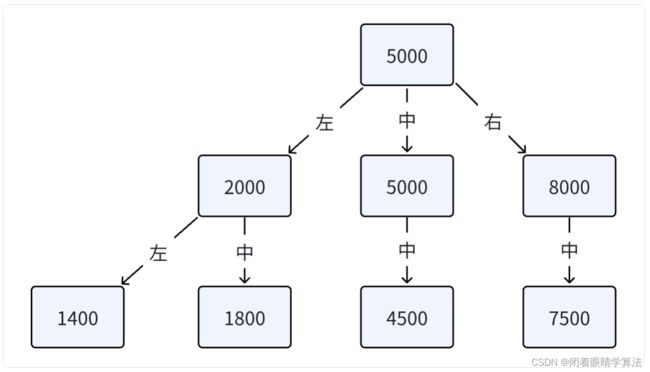
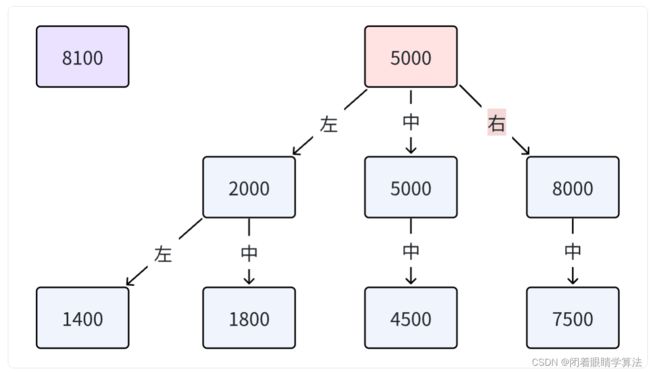
假设此时这棵三叉搜索树已经构建了一部分。譬如

此时我们要往这棵树中插入值为8100的节点，其过程应为：

1. 从根节点5000出发，比较5000和8100之间的大小关系。8100 - 5000 > 500，故该节点应该位于根节点5000的右子树中。

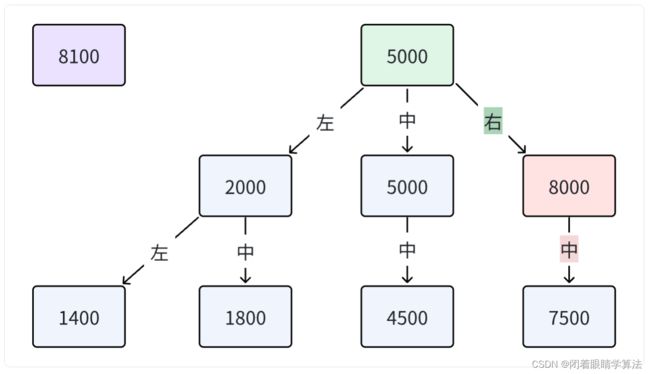
2. 发现根节点5000的右节点8000已经存在，则进行递归，进一步比较8000和8100之间的大小关系。abs(8100 - 8000) <= 500，故该节点应该位于节点8000的中间子树中。

3. 发现节点8000的中间节点7500已经存在，则进行递归，进一步比较7500和8100之间的大小关系。8100 - 7500 > 500，故该节点应该位于节点7500的右子树中。

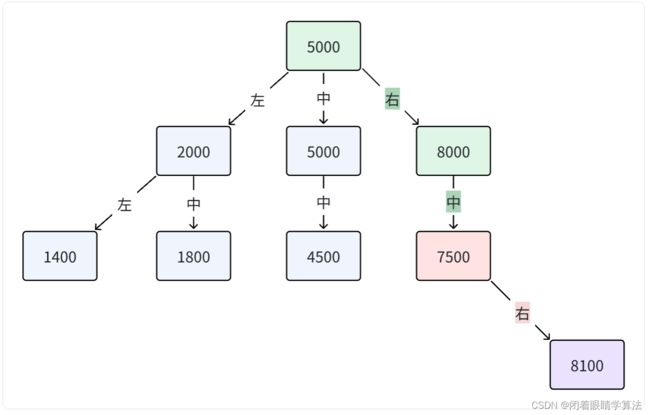
4. 发现节点7500的右节点为空，此时将值为8100的节点插入节点7500的右节点。这样就完成了搜索树的插入操作。

三叉搜索树的节点插入过程（递归三要素）

注意到上述每一步的过程都是类似的，显然可以用递归来实现。考虑递归三要素。

1. 递归子问题
   • 插入节点insert_node的值insert_node.val和当前节点cur_node的值cur_node.val比较。若
     • insert_node.val - cur_node.val > 500，则插入节点insert_node应该位于当前节点cur_node的右子树的位置。若此时cur_node的右节点cur_node.right不为空，则对cur_node.right进行递归调用。
     • insert_node.val - cur_node.val < -500，则插入节点insert_node应该位于当前节点cur_node的左子树的位置。若此时cur_node的左节点cur_node.left不为空，则对cur_node.left进行递归调用。
     • abs(insert_node.val - cur_node.val) < 500，则插入节点insert_node应该位于当前节点cur_node的中间子树的位置。若此时cur_node的中间节点cur_mid.left不为空，则对cur_node.mid进行递归调用。
2. 递归终止条件
   • 做完上述判断后，若当前节点cur_node的对应子节点为空，说明insert_node可以插入在cur_node的对应节点位置。插入完毕，递归终止。
3. 递归入口
   • 除了根节点，其他节点都要从根节点出发进行比较和判断，故递归入口为插入节点insert_node和根节点root进行比较。

想清楚上述过程之后，建树的大致框架就已经能够完成了。其代码如下：

def dfs(cur_node, val):
    if cur_node.val - val < -500:
        if cur_node.left is None:
            cur_node.left = Node(val)
            return
        dfs(cur_node.left, val)
    elif cur_node.val - val > 500:
        if cur_node.right is None:
            cur_node.right = Node(val)
            return
        dfs(cur_node.right, val)
    else:
        if cur_node.mid is None:
            cur_node.mid = Node(val)
            return
        dfs(cur_node.mid, val)

上述过程的单次时间复杂度为O(logn)，由于对于的每一个新插入的val都必须调用上述

计算树的高度

注意本题的设问是计算树的高度。这个问题有两种解决方案，同学们可以自行选择自己喜欢的方案来进行。在效率上，前者是略微优于后者的，因此后者需要在建树结束之后，对整棵树再做一次时间复杂度为O(n)的遍历，但总时间复杂度不变。

在建树过程中计算树的高度

可以在递归函数中多维护一个变量cur_depth表示当前节点cur_node的深度，同时维护一个全局变量ans表示全局的最大深度，一边建树一遍同时更新当前树的最大高度。

在对子节点进行递归调用时，由于子节点的高度始终比当前节点大1，所以应该将cur_depth+1作为子节点的高度传入递归函数中。

在递归终止即进行节点插入时，进行ans和cur_depth+1的比较。之所以是cur_depth+1，是因为进行节点插入后，该节点插入后的高度应该比当前节点高度+1。故dfs()递归函数可以修改为

def dfs(cur_node, val, cur_depth):
    global ans
    if cur_node.val - val < -500:
        if cur_node.left is None:
            cur_node.left = Node(val)
            ans = max(ans, cur_depth + 1)
            return
        dfs(cur_node.left, val, cur_depth + 1)
    elif cur_node.val - val > 500:
        if cur_node.right is None:
            cur_node.right = Node(val)
            ans = max(ans, cur_depth + 1)
            return
        dfs(cur_node.right, val, cur_depth + 1)
    else:
        if cur_node.mid is None:
            cur_node.mid = Node(val)
            ans = max(ans, cur_depth + 1)
            return
        dfs(cur_node.mid, val, cur_depth + 1)

在建树完毕后计算树的高度

同样使用递归完成。其过程类似于LeetCode104. 二叉树的最大深度。其核心的递归函数代码如下

def dfs_cal_height(node, cur_depth):
    if node == None:
        return
    global ans
    ans = max(cur_depth, ans)
    dfs_cal_height(node.left, cur_depth+1)
    dfs_cal_height(node.mid, cur_depth+1)
    dfs_cal_height(node.right, cur_depth+1)

代码

解法一：建树过程中计算树的高度

python

# 题目：【DFS】2023C-计算三叉搜索树的高度
# 分值：200
# 作者：闭着眼睛学数理化
# 算法：DFS/树（解法一：建树过程中计算树的高度）
# 代码看不懂的地方，请直接在群上提问


# 构建树节点类
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.mid = None
        self.right = None


# 创建dfs函数，用于对树插入值为val的节点
# 参数cur_node表示与val进行比较的当前节点
# 参数cur_depth表示当前深度
def dfs(cur_node, val, cur_depth):
    global ans
    # 插入节点insert_node位于当前节点cur_node左子树的情况
    if cur_node.val - val < -500:
        # 若cur_node的左节点不存在，则新建插入节点
        # insert_node = Node(val)
        # 并将其插入cur_node的左节点中
        if cur_node.left is None:
            cur_node.left = Node(val)
            # 插入该节点后，最终深度为当前深度+1，故ans应该与cur_depth+1进行比较
            ans = max(ans, cur_depth + 1)
            return
        # 否则对左节点进行递归调用，继续比较，同时深度+1
        dfs(cur_node.left, val, cur_depth + 1)
    # 插入节点insert_node位于当前节点cur_node右子树的情况
    elif cur_node.val - val > 500:
        # 若cur_node的右节点不存在，则新建插入节点
        # insert_node = Node(val)
        # 并将其插入cur_node的右节点中
        if cur_node.right is None:
            cur_node.right = Node(val)
            # 插入该节点后，最终深度为当前深度+1，故ans应该与cur_depth+1进行比较
            ans = max(ans, cur_depth + 1)
            return
        # 否则对右节点进行递归调用，继续比较，同时深度+1
        dfs(cur_node.right, val, cur_depth + 1)
    # 插入节点insert_node位于当前节点cur_node中间子树的情况
    else:
        # 若cur_node的终极那节点不存在，则新建插入节点
        # insert_node = Node(val)
        # 并将其插入cur_node的中间节点中
        if cur_node.mid is None:
            cur_node.mid = Node(val)
            # 插入该节点后，最终深度为当前深度+1，故ans应该与cur_depth+1进行比较
            ans = max(ans, cur_depth + 1)
            return
        # 否则对中间节点进行递归调用，继续比较，同时深度+1
        dfs(cur_node.mid, val, cur_depth + 1)


# 输入节点数目n
n = int(input())
# 输入节点值数组vals
vals = list(map(int, input().split()))
# 构建根节点，根节点的值一定为vals数组中的第一个元素
root = Node(vals[0])
# 答案变量
ans = 1
# 遍历除了根节点以外的其他节点的值val
# 这个值对应插入节点insert_node
for val in vals[1:]:
    # 对于每一个节点的值val，都调用dfs函数
    # 递归入口传入根节点root，插入新的值为val的节点
    # 当前深度为1
    dfs(root, val, 1)

print(ans)

java

import java.util.Scanner;

class Node {
    int val;
    Node left, mid, right;

    Node(int val) {
        this.val = val;
        this.left = null;
        this.mid = null;
        this.right = null;
    }
}

public class Main {
    static int ans = 1;

    static void dfs(Node curNode, int val, int curDepth) {
        if (curNode.val - val < -500) {
            if (curNode.left == null) {
                curNode.left = new Node(val);
                ans = Math.max(ans, curDepth + 1);
                return;
            }
            dfs(curNode.left, val, curDepth + 1);
        } else if (curNode.val - val > 500) {
            if (curNode.right == null) {
                curNode.right = new Node(val);
                ans = Math.max(ans, curDepth + 1);
                return;
            }
            dfs(curNode.right, val, curDepth + 1);
        } else {
            if (curNode.mid == null) {
                curNode.mid = new Node(val);
                ans = Math.max(ans, curDepth + 1);
                return;
            }
            dfs(curNode.mid, val, curDepth + 1);
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int[] vals = new int[n];
        for (int i = 0; i < n; i++) {
            vals[i] = scanner.nextInt();
        }

        Node root = new Node(vals[0]);
        for (int i = 1; i < n; i++) {
            dfs(root, vals[i], 1);
        }

        System.out.println(ans);
    }
}

cpp

#include 
#include 

using namespace std;

struct Node {
    int val;
    Node* left;
    Node* mid;
    Node* right;

    Node(int val) : val(val), left(nullptr), mid(nullptr), right(nullptr) {}
};

int ans = 1;

void dfs(Node* curNode, int val, int curDepth) {
    if (curNode->val - val < -500) {
        if (curNode->left == nullptr) {
            curNode->left = new Node(val);
            ans = max(ans, curDepth + 1);
            return;
        }
        dfs(curNode->left, val, curDepth + 1);
    } else if (curNode->val - val > 500) {
        if (curNode->right == nullptr) {
            curNode->right = new Node(val);
            ans = max(ans, curDepth + 1);
            return;
        }
        dfs(curNode->right, val, curDepth + 1);
    } else {
        if (curNode->mid == nullptr) {
            curNode->mid = new Node(val);
            ans = max(ans, curDepth + 1);
            return;
        }
        dfs(curNode->mid, val, curDepth + 1);
    }
}

int main() {
    int n;
    cin >> n;
    vector<int> vals(n);
    for (int i = 0; i < n; i++) {
        cin >> vals[i];
    }

    Node* root = new Node(vals[0]);
    for (int i = 1; i < n; i++) {
        dfs(root, vals[i], 1);
    }

    cout << ans << endl;

    return 0;
}

解法二：建树完毕后计算树的高度

python

# 题目：【DFS】2023C-计算三叉搜索树的高度
# 分值：200
# 作者：闭着眼睛学数理化
# 算法：DFS/树（解法二：建树完毕后计算树的高度）
# 代码看不懂的地方，请直接在群上提问


# 构建树节点类
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.mid = None
        self.right = None


# 创建dfs函数，用于对树插入值为val的节点
# 参数cur_node表示与val进行比较的当前节点
def dfs(cur_node, val):
    # 插入节点insert_node位于当前节点cur_node左子树的情况
    if cur_node.val - val < -500:
        # 若cur_node的左节点不存在，则新建插入节点
        # insert_node = Node(val)
        # 并将其插入cur_node的左节点中
        if cur_node.left is None:
            cur_node.left = Node(val)
            return
        # 否则对左节点进行递归调用，继续比较
        dfs(cur_node.left, val)
    # 插入节点insert_node位于当前节点cur_node右子树的情况
    elif cur_node.val - val > 500:
        # 若cur_node的右节点不存在，则新建插入节点
        # insert_node = Node(val)
        # 并将其插入cur_node的右节点中
        if cur_node.right is None:
            cur_node.right = Node(val)
            return
        # 否则对右节点进行递归调用，继续比较
        dfs(cur_node.right, val)
    # 插入节点insert_node位于当前节点cur_node中间子树的情况
    else:
        # 若cur_node的终极那节点不存在，则新建插入节点
        # insert_node = Node(val)
        # 并将其插入cur_node的中间节点中
        if cur_node.mid is None:
            cur_node.mid = Node(val)
            return
        # 否则对中间节点进行递归调用，继续比较
        dfs(cur_node.mid, val)


# 用于计算树高度的递归函数
# node为当前节点，cur_depth为当前高度
def dfs_cal_height(node, cur_depth):
    if node == None:
        return
    global ans
    ans = max(cur_depth, ans)
    dfs_cal_height(node.left, cur_depth+1)
    dfs_cal_height(node.mid, cur_depth+1)
    dfs_cal_height(node.right, cur_depth+1)


# 输入节点数目n
n = int(input())
# 输入节点值数组vals
vals = list(map(int, input().split()))
# 构建根节点，根节点的值一定为vals数组中的第一个元素
root = Node(vals[0])

# 遍历除了根节点以外的其他节点的值val
# 这个值对应插入节点insert_node
for val in vals[1:]:
    # 对于每一个节点的值val，都调用dfs函数
    # 递归入口传入根节点root，插入新的值为val的节点
    dfs(root, val)


ans = 1
# 计算树的高度的函数，递归调用一次即可，传入节点为根节点和起始高度1
dfs_cal_height(root, 1)

print(ans)

java

import java.util.Scanner;

class Main {
    static class Node {
        int val;
        Node left, mid, right;

        Node(int val) {
            this.val = val;
        }
    }

    static int ans = 1;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int[] vals = new int[n];
        for (int i = 0; i < n; i++) {
            vals[i] = scanner.nextInt();
        }

        Node root = new Node(vals[0]);

        for (int i = 1; i < n; i++) {
            dfs(root, vals[i]);
        }

        dfs_cal_height(root, 1);

        System.out.println(ans);
    }

    static void dfs(Node curNode, int val) {
        if (curNode.val - val < -500) {
            if (curNode.left == null) {
                curNode.left = new Node(val);
                return;
            }
            dfs(curNode.left, val);
        } else if (curNode.val - val > 500) {
            if (curNode.right == null) {
                curNode.right = new Node(val);
                return;
            }
            dfs(curNode.right, val);
        } else {
            if (curNode.mid == null) {
                curNode.mid = new Node(val);
                return;
            }
            dfs(curNode.mid, val);
        }
    }

    static void dfs_cal_height(Node node, int curDepth) {
        if (node == null) {
            return;
        }
        ans = Math.max(curDepth, ans);
        dfs_cal_height(node.left, curDepth + 1);
        dfs_cal_height(node.mid, curDepth + 1);
        dfs_cal_height(node.right, curDepth + 1);
    }
}

cpp

#include 
#include 
using namespace std;

class Node {
public:
    int val;
    Node* left;
    Node* mid;
    Node* right;

    Node(int val) {
        this->val = val;
        left = nullptr;
        mid = nullptr;
        right = nullptr;
    }
};

int ans = 1;

void dfs(Node* curNode, int val) {
    if (curNode->val - val < -500) {
        if (curNode->left == nullptr) {
            curNode->left = new Node(val);
            return;
        }
        dfs(curNode->left, val);
    } else if (curNode->val - val > 500) {
        if (curNode->right == nullptr) {
            curNode->right = new Node(val);
            return;
        }
        dfs(curNode->right, val);
    } else {
        if (curNode->mid == nullptr) {
            curNode->mid = new Node(val);
            return;
        }
        dfs(curNode->mid, val);
    }
}

void dfs_cal_height(Node* node, int curDepth) {
    if (node == nullptr) {
        return;
    }
    ans = max(curDepth, ans);
    dfs_cal_height(node->left, curDepth + 1);
    dfs_cal_height(node->mid, curDepth + 1);
    dfs_cal_height(node->right, curDepth + 1);
}

int main() {
    int n;
    cin >> n;
    vector<int> vals(n);

    for (int i = 0; i < n; i++) {
        cin >> vals[i];
    }

    Node* root = new Node(vals[0]);

    for (int i = 1; i < n; i++) {
        dfs(root, vals[i]);
    }

    dfs_cal_height(root, 1);

    cout << ans << endl;

    return 0;
}

时空复杂度

时间复杂度：O(NlogN)。建树的时间复杂度。

空间复杂度：O(N)。树所占空间。

---

华为OD算法/大厂面试高频题算法练习冲刺训练

• 华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名！目前已服务100+同学成功上岸！

• 课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化

• 每期人数维持在20人内，保证能够最大限度地满足到每一个同学的需求，达到和1v1同样的学习效果！

• 60+天陪伴式学习，40+直播课时，300+动画图解视频，300+LeetCode经典题，200+华为OD真题/大厂真题，还有简历修改、模拟面试、专属HR对接将为你解锁

• 可上全网独家的欧弟OJ系统练习华子OD、大厂真题

• 可查看链接 大厂真题汇总 & OD真题汇总(持续更新)

• 绿色聊天软件戳 od1336了解更多