LeetCode解法汇总1631. 最小体力消耗路径

 目录链接：

力扣编程题-解法汇总_分享+记录-CSDN博客

GitHub同步刷题项目：

https://github.com/September26/java-algorithms

原题链接：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

描述：

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

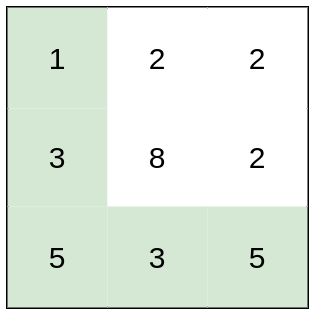
示例 1：

输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

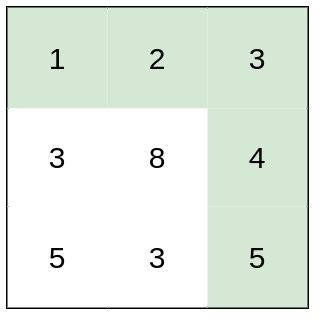
示例 2：

输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

解题思路：

典型的贪心算法。构建一个priority_queue队列，队列中排序靠前的是差值较小的。队列中的位置，代表是贪心算法还未遍历到的额位置，如果遍历到某个位置，则把对应位置设置为差值，比如dp[y][x]=10这样。

然后选择从这个位置可以到达到的所有位置（如果已经达到过则跳过，因为该位置已经不属于最优解了），并且计算出差值，加入到队列中。直到遍历到终点结束。

代码：

bool cmp(pair> &a, pair> &b)
{
    return a.first > b.first;
}

class Solution {
private:
    static constexpr int forwards[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};


public:
    bool getMinHeight(int fx, int fy, int x, int y, vector> &dp, vector> &heights)
    {
        if (x < 0 || x == heights[0].size())
        {
            return false;
        }
        if (y < 0 || y == heights.size())
        {
            return false;
        }
        if (dp[y][x] >= 0)
        {
            return false;
        }
        return true;
    }

    int minimumEffortPath(vector> &heights)
    {
        int ySize = heights.size();
        int xSize = heights[0].size();
        vector> dp(ySize);
        for (int i = 0; i < ySize; i++)
        {
            for (int j = 0; j < xSize; j++)
            {
                dp[i].push_back(-1);
            }
        }

        // 使用函数指针作为比较函数
        priority_queue>, vector>>, decltype(&cmp)> queue(cmp);
        queue.push({0, {0, 0}});
        dp[0][0] = 0;
        vector> forwards = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        while (!queue.empty())
        {
            pair> top = queue.top();
            int x = top.second.first;
            int y = top.second.second;
            int value = top.first;
            dp[y][x] = top.first;
            queue.pop();
            if (x == xSize - 1 && y == ySize - 1)
            {
                break;
            }
            if (x == 2 && y == 1)
            {
                cout << "1" << endl;
            }
            for (vector forward : forwards)
            {
                int newX = x + forward[0];
                int newY = y + forward[1];
                if (getMinHeight(x, y, newX, newY, dp, heights))
                {
                    pair> nextNode = make_pair(max(value, abs(heights[newY][newX] - heights[y][x])), make_pair(newX, newY));
                    queue.push(nextNode);
                }
            }
        }
        return dp[ySize - 1][xSize - 1];
    }
};