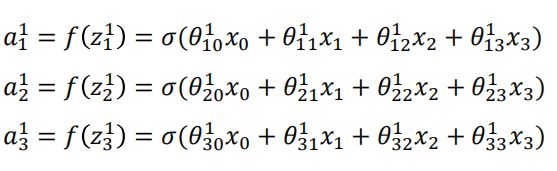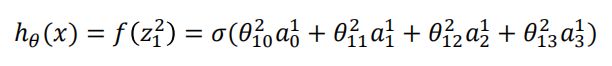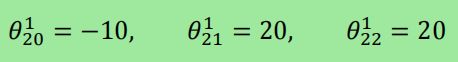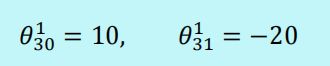Neural Network——神经网络

1.feature reusing——特征复用

1.1 什么是特征复用

        回顾我们之前所学习的模型，本质上都是基于线性回归，但却都可以运用于非线性相关的数据，包括使用了如下方法

• 增加更多的特征
• 产生新的特征（多项式回归）
• 核函数

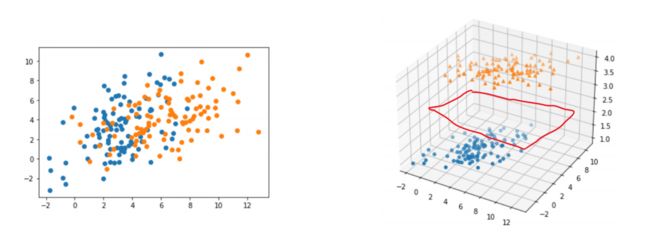
        在本身的维度找不到线性决策边界，但通过非线性转换将特征映射到高维空间在某个高纬度空间可以找到一个线性决策边界，同时它对应着其本身的维度的非线性决策边界。如下图示例

        我们可以多次进行这样的转换，以实现更好（更稳健）的决策边界，这种技术称为特征复用，神经网络就是特征重用思想的一种实例化。

1.2 为什么需要特征复用

        假设我们希望训练一个模型来识别识别一张图片上是否是一辆汽车，一种方法是我们利用很多汽车的图片和很多非汽车的图片，然后利用这些图片上一个个像素的值来作为特征。

        假如我们只选用灰度图片，每个像素则只有一个值，我们可以选取图片上的两个不同位置上的两个像素，然后训练一个逻辑回归算法利用这两个像素的值来判断图片上是否是汽车

        假使我们采用的都是50x50像素的小图片，则会有2500个特征，如果我们要进一步将两两特征组合构成一个多项式模型，则会有约25002/2个（接近3百万个）特征。普通的逻辑回归模型，不能有效地处理这么多的特征，计算量非常的大。

        

问题：

• 特征很敏感，例如同一辆汽车，一张照片在不同时间、不同环境下拍摄出来的照片都不一样；这样导致模型不具有鲁棒性
• 特征维度过高，计算量非常的大

鲁棒性（Robustness）指的是一个模型对于数据中的噪声、异常值或其他干扰因素的抵抗能力，可以理解为低方差

通过特征复用，可以让特征不会处于如此高维空间，而且具有更好鲁棒性

2.Neural Network

2.1 神经网络的结构

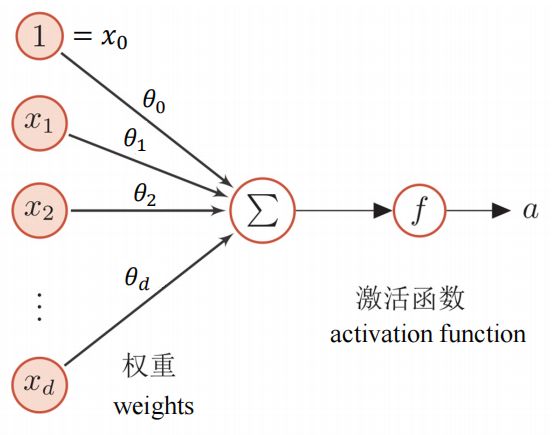
       特征向量X进入一个神经元后，先经过一次线性变换，然后再通过一个激活函数（activation function）进行非线性变换得到输出

        回顾逻辑回归的结构，（Sigmoid就是逻辑回归的激活函数）

        

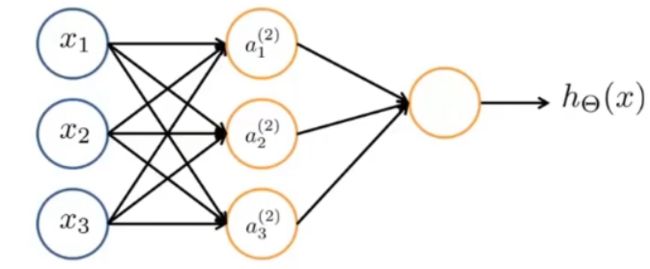
        相当于只有一个神经元，于是我们将其拓展，使用更多的神经元，，并且输入数据与每个神经元都进行连接，我们就可以得到一个简单的三层神经网络，这就是它比线性回归和逻辑回归强的原因

                

        

        这个神经网络共有三层，第一层也叫输入层，第二层也叫隐藏层(除了输入层和输出层都叫隐藏层，因为在训练时我们只能看见输入和输出)，最后一层为输出层。

        输入的每一个x均和每个神经元进行连接，故这种结构的隐藏层也叫全连接层。也叫原始输入数据的特征向量。像这种传输从输入到输出单方向的神经网络也叫前馈神经网络（feedforward network）

        如今的神经网络包含若干隐藏层，每个隐藏层都包含若干个神经元，输出层的大小也和想要实现的任务有关。越深层的网络能拟合越复杂的函数，学习到对象更本质的特征。

2.2 前向传播（forward propaganda）的计算过程

        以这个网络结构为例

        其中的值恒为1，相当于偏置项，其中的值恒为1,相当于偏置神经元，则其不参与这层的输入计算，不画出也可以，那么偏置参数b向量就和权重参数在同一个神经元里。

        根据逻辑回归的模型来说，如果（）连接一个神经元就会对应有四个权重（其中一个与相乘为偏置项），这些参数存储在神经元中，如果对应的为，那么我们就可以得到隐藏层权重如下表示，隐藏层输入为1×3，输出为3×3，所以权重矩阵大小为3×3

                                

        第i列分别对应着

        假设激活函数用()表示，我们可以得到隐藏层的输出

        

        如果写成矩阵的形式

        

• 通常只有一行的行向量都会写成列向量
• 通常是参数矩阵转置后与输入相乘

        接着对于输入层输入来说，也有权重矩阵，输入为4×1（这里加上了偏置神经元），输出为1×1，所以权重矩阵大小为4×1（转置后变成行向量1×4与输入相乘）

        

        于是我们可以得到这个神经网络最终输出

        

…………………………………………………………………………………………………………………

来看一个更复杂的网络结构       

        这是一个实现手写体数字识别神经网络，包含二个隐藏层，都为全连接结构，神经元个数分别为1000，2000，最后输出层为大小为10，对应给出10个数字概率

        输入手写体数字图片大小为28*28（这是一个黑白图，所以只有一个颜色通道），该图片会展平成784*1作为输入。那么根据输入大小与输出大小还有矩阵乘法我们可以得到，第一个隐藏层权重矩阵大小为784*1000

        

        同样的第二个隐藏层权重矩阵大小为1000*2000

        输出层权重矩阵大小为1000*10，此外为了实现多分类，在最后使用了Softmax函数

        假设网络预测这个输入为数字“9”，那么最终的输出≈[0,0,0,0,0,0,0,0,1]（相当于one-hot编码）

2.3 为什么神经网络可以拟合非线性数据

        假设我们有这样一个异或问题（XOR），输入数据为一对二进制编码，相异输出1，相同输出0，如下图。异或问题就是一个经典的非线性问题，我们无法使用一个直线来完全分开这两类数据

                                

        当然我们可以使用曲线将其分开

                        

        当然同或（XNOR）是类似的，同或会在输入相同才输出1，相异输出0

        接下来我们使用一个简单神经网络就可以解决这个问题，在解决异或问题先，我们先解决别的问题

1.与（and）操作

        与操作只有当输入都为1时，才会输出1，否则为0  

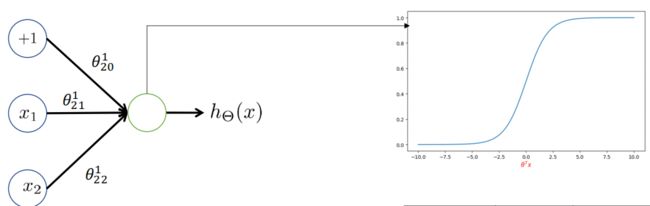
        我们可以构建这样一个结构就可以实现与操作，使用sigmoid作为激活函数，假设网络通过学习得到了参数组为

        

        

        输入不同的组合，可以看到是正确的

        

2.或（or）操作

        或操作只要输入有一个1，那么就会输出1

        同样的

        假设网络通过学习得到了参数组为

        

                

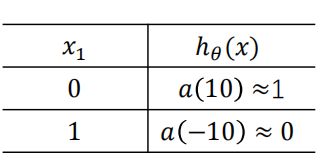
3.非（not）操作

        非操作会将输入置反

         假设网络通过学习得到了参数组为

        

                        

4.异或

        我们可以将这几个结构进行组合

        构建一个两层的神经网络

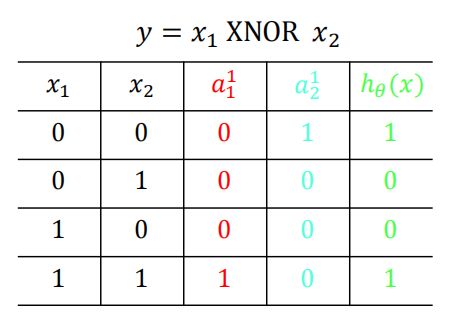
        假设通过学习得到了图上的参数，我们就可以解决同或问题

        

        对于异或结构是一样的，在学习时改变输入对应输出的标签就行，学习到不一样的参数组。

                ​​​​​​​        ​​​​​​​        ​​​​​​​        

2.4 反向传播（backpropagation）

        神经网络中的参数并不是随机的，而是和之前学习的模型一样需要通过训练数据学习，这样这些参数才有意义。为此我们需要计算各参数梯度，神经网络通过前向传播从输入到输出，通过反向传播从后往前计算传回参数梯度。

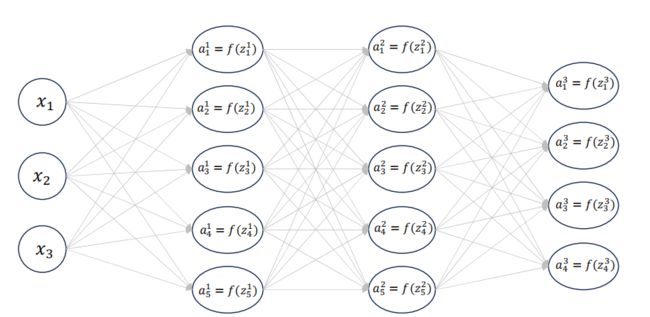
        假设我们有这样一个网络结构

        ​​​​​​​                ​​​​​​​

        各层输入输出如下

                ​​​​​​​

反向传播基于链式求导法则

        假设损失函数表示为，激活函数为sigmoid

（待更新）

2.5 激活函数

        引入非线性激活函数后，使网络可以逼近任意非线性函数。如果不加上激活函数，虽然有多层网络，多神经元，但所有线性变换的叠加仍然是线性函数。

常见的激活函数有：Relu函数、sigmoid函数以及tanh函数。

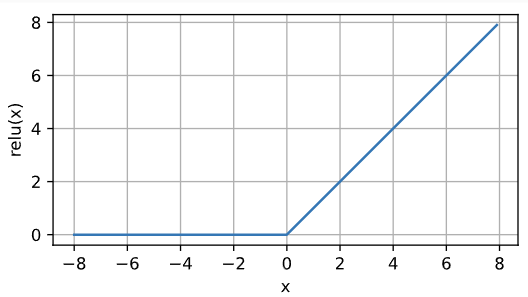
1. Relu函数

        

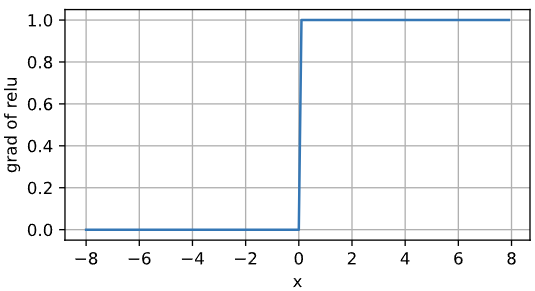
Relu(x) = max(x,0)，计算非常简单

其导函数图像为：

        

不存在梯度消失现象。因此ReLU比起其他几个更常用

2. Sigmoid函数

    

Sigmoid函数可以将输入的任何值映射到（0，1）。注意，当输入接近0时，sigmoid函数接近线性变换

导函数图像如下：

               

        当输入为0时，sigmoid函数的导数达到最大值0.25； 而输入在任一方向上越远离0点时，导数越接近0（饱和区梯度消失现象）,此时不利于参数更新。

3. tanh函数（双曲正切函数）

                        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

tanh函数可以将输入的任何值映射到（-1，1）

        ​​​​​​​    

        注意，当输入在0附近时，tanh函数接近线性变换。 函数的形状类似于sigmoid函数， 不同的是tanh函数关于坐标系原点中心对称

导函数图像如下图所示：

        ​​​​​​​      

        当输入接近0时，tanh函数的导数接近最大值1。同样存在饱和区梯度消失现象。