课题学习(十六)----阅读《Continuous Wellbore Surveying While Drilling Utilizing MEMS Gyroscopes Based...》论文

   论文全称：《Continuous Wellbore Surveying While Drilling Utilizing MEMS Gyroscopes
Based on Kalman Filtering 》
摘要：

   目前在钻井过程中计算井筒的方法是基于在所需位置的固定测量。这是通过测量当前和先前测量站之间钻孔的倾角和方位角来完成的。利用基于钻孔形状假设的数学模型，可以推导出井眼坐标。目前的方法忽略了两个测量站之间的实际轨迹。
   勘探和生产公司需要具有成本效益的钻井作业。因此，对捕捉固定测量站之间实际轨迹的连续测量的需求一直在上升。这提供了沿井眼轨迹“狗腿”曲率的实际估计。此外，这可以更好地估计井眼的套管和固井情况。因此，在此开发中，使用三个加速度计和三个MEMS陀螺仪连续测量两个测量站之间的井眼轨迹。计算算法基于捷联惯导系统力学编排和卡尔曼滤波。
   连续钻井测量系统的输入是加速度计和陀螺仪测量值，输出是钻头的位置、工具面、倾角和方位角。如果没有外部观测来更新测量系统，该井眼测量系统的位置和方位角误差会无限增长。两个外部更新方案可以在钻孔时限制这种错误的增长。第一种方法是基于钻杆长度测量的连续源，第二种方法是零速度更新。卡尔曼滤波连续测量系统成功地应用于钻井试验。
   利用钻杆长度的外部更新来减小测量误差漂移。当钻井过程停止连接新的钻杆架时，卡尔曼滤波器采用零速度更新。

一、论文内容介绍

1.1 方法

   当在MWD工具内安装MEMS陀螺仪和加速度计时，加速度计三位一体测量钻头在三个正交方向上的加速度，加速度计的敏感轴方向与MWD工具的轴方向重合。在这个阶段，所有的测量都将参考这些轴，这些轴被称为载体系。
   除了加速度计测量外，陀螺仪测量对于确定钻头相对于导航系的方向也是必不可少的。这是通过整合陀螺仪测量和初始姿态角的知识来实现的，这些姿态角包括俯仰、滚动和方位角。为了将加速度计的测量值从载体系转换到导航系（b–>n），需要知道姿态角。如果已知钻头在三个正交方向上的初始速度，则可以通过变换后的每个加速度分量的时间积分来确定导航系中的连续速度。第二积分导出相对于初始位置的导航系中的钻头位置。
   加速度计的读数受到地球引力场的影响。重力加速度被加到加速度计的测量值中。因此，知道加速度计所在位置的地球重力加速度是至关重要的。这将分离由地球引力引起的加速度和由钻柱运动引起的加速度。

1.2 坐标系间的变换

   加速度计和陀螺仪传感器安装在MWD工具内，其敏感轴分别垂直于xy平面的正方向(Forward Direction -->y)、横方向(Transverse–>x)和z(up/dowm Direction)方向。这三个轴构成了载体系(b系)。MWD工具内的b系如下所示：

   因此，原来的加速度计和陀螺仪测量值表示b系中的线加速度和角速度。然而，为了提供移动钻头和钻铤的位置、速度和姿态，测量结果通常会转换为导航参考系。选择n系的主要好处是，钻铤的方位角、倾角和工具面角直接作为n系中惯导系统力学编排的输出。使用n系的另一个优点是东北面导航参数的计算误差被限制，在那里它们耦合并产生舒勒循环。这些误差以1/ 5000hz的舒勒频率振荡。
  加速度计和陀螺仪测量在载体系(b系)中进行。矩阵$R_b^n$用于将这些测量值转换为导航系。$R_b^n$是方位角(ψ)，俯仰角(θ)和工具面角(ξ)的组合;表述如下:
R b n = ( c o s Ψ c o s ξ + s i n Ψ s i n θ s i n ξ s i n Ψ c o s θ c o s Ψ c o s ξ − s i n Ψ s i n θ c o s ξ − s i n Ψ c o s ξ + c o s Ψ s i n θ s i n ξ c o s Ψ c o s θ − s i n Ψ s i n ξ − c o s Ψ s i n θ c o s ξ − c o s θ s i n ξ s i n θ c o s θ c o s ξ ) R_b^n=\begin{pmatrix} cos\Psi cos\xi+sin\Psi sin\theta sin\xi &sin\Psi cos\theta &cos\Psi cos\xi-sin\Psi sin\theta cos\xi \\ -sin\Psi cos\xi+cos\Psi sin\theta sin\xi &cos\Psi cos\theta &-sin\Psi sin\xi-cos\Psi sin\theta cos\xi \\ -cos\theta sin\xi &sin\theta &cos\theta cos\xi \end{pmatrix} Rbn​= ​cosΨcosξ+sinΨsinθsinξ−sinΨcosξ+cosΨsinθsinξ−cosθsinξ​sinΨcosθcosΨcosθsinθ​cosΨcosξ−sinΨsinθcosξ−sinΨsinξ−cosΨsinθcosξcosθcosξ​ ​
  因此，测量值从n系到b系的变换可以通过变换矩阵$R_b^n$的逆来实现。

1.3 力学编排

   惯性测量单元提供了在工具体框架内测量的三个角速度${\omega }_{ib}^b={\left(\begin{array}{ccc}{\omega }_x& {\omega }_y& {\omega }_z\end{array}\right)}^T$和三个加速度$f^b={\left(\begin{array}{ccc}{f}_x& f_y& f_z\end{array}\right)}^T$。然后使用旋转(方向余弦)矩阵将比力$f^b$投影到导航框架上。然后，角增量${\theta }_{ib}^b={\left(\begin{array}{ccc}\Delta {\theta }_x& \Delta {\theta }_y& \Delta {\theta }_z\end{array}\right)}^T$可以用角速度测量来确定。线速度增量$\left(\begin{array}{ccc}\Delta V_x& \Delta V_y& \Delta V_z\end{array}\right)$用三轴加速度测量得到。
  所导出的角增量捕获除了地球自转和导航系相对于地球系的方向变化之外的钻铤角增量。最后两种影响必须考虑在内。它们的表达式${\omega }_{in}^b$中的表达式由方程2推导出来。然后可以将给定时间$t_k$的角增量表示为下式:
θ i n b ( t k ) = ω i n b ( t k ) Δ t = R n b ( t k ) ( − V n ( t k ) M + h V e ( t k ) N + h + ω e c o s ϕ V e ( t k ) t a n ϕ N + h + ω e s i n ϕ ) Δ t \theta_{in}^b(t_k)=\omega_{in}^b(t_k)\Delta t=R_n^b(t_k)\begin{pmatrix}\frac{-V^n(t_k)}{M+h}\\ \frac{V^e(t_k)}{N+h}+\omega^ecos\phi \\ \frac{V^e(t_k)tan\phi}{N+h}+\omega^esin\phi \end{pmatrix}\Delta t θinb​(tk​)=ωinb​(tk​)Δt=Rnb​(tk​) ​M+h−Vn(tk​)​N+hVe(tk​)​+ωecosϕN+hVe(tk​)tanϕ​+ωesinϕ​ ​Δt
  在此说明一下：$M+h$记作$R_M$，为沿子午圈的曲率半径，$N+h$记作$R_N$ ，为沿卯酉圈的曲率半径 。具体可参考秦永元老师《惯性导航》第七章。
  现在可以通过从原始的${\theta }_{ib}^b(t_k)$中减去并补偿${\theta }_{in}^b(t_k)$来确定给定时间${\theta }_{nb}^b(t_k)$钻柱的实际角增量，如下所示: θ n b b ( t k ) = θ i b b ( t k ) − θ i n b ( t k ) = ( Δ θ x Δ θ y Δ θ z ) \theta_{nb}^b(t_k)=\theta_{ib}^b(t_k)-\theta_{in}^b(t_k)=\begin{pmatrix}\Delta\theta_x \\ \Delta\theta_y \\\Delta\theta_z\end{pmatrix} θnbb​(tk​)=θibb​(tk​)−θinb​(tk​)= ​Δθx​Δθy​Δθz​​ ​
  下面的步骤更新四元数向量。初始四元数向量$Q(t_0)$是使用初始旋转矩阵$R_N^b(t_0)$来计算的，该矩阵是由平稳周期内的初始对齐导出的。四元数向量通过使用下面的公式更新为:
( q 1 ( t k + 1 ) q 2 ( t k + 1 ) q 3 ( t k + 1 ) q 4 ( t k + 1 ) ) = ( q 1 ( t k ) q 2 ( t k ) q 3 ( t k ) q 4 ( t k ) ) + 1 2 ( 0 Δ θ z − Δ θ y Δ θ x − Δ θ z 0 Δ θ x Δ θ y Δ θ y − Δ θ x 0 Δ θ z − Δ θ x − Δ θ y − Δ θ z 0 ) ( q 1 ( t k ) q 2 ( t k ) q 3 ( t k ) q 4 ( t k ) ) \begin{pmatrix}q_1(t_{k+1}) \\ q_2(t_{k+1})\\q_3(t_{k+1})\\q_4(t_{k+1})\end{pmatrix}= \begin{pmatrix}q_1(t_{k}) \\ q_2(t_{k})\\q_3(t_{k})\\q_4(t_{k})\end{pmatrix}+\frac{1}{2}\begin{pmatrix} 0&\Delta\theta_z&-\Delta\theta_y&\Delta\theta_x \\ -\Delta\theta_z&0&\Delta\theta_x&\Delta\theta_y\\ \Delta\theta_y&-\Delta\theta_x&0&\Delta\theta_z\\ -\Delta\theta_x&-\Delta\theta_y&-\Delta\theta_z&0\end{pmatrix}\begin{pmatrix}q_1(t_{k}) \\ q_2(t_{k})\\q_3(t_{k})\\q_4(t_{k})\end{pmatrix} ​q1​(tk+1​)q2​(tk+1​)q3​(tk+1​)q4​(tk+1​)​ ​= ​q1​(tk​)q2​(tk​)q3​(tk​)q4​(tk​)​ ​+21​ ​0−Δθz​Δθy​−Δθx​​Δθz​0−Δθx​−Δθy​​−Δθy​Δθx​0−Δθz​​Δθx​Δθy​Δθz​0​ ​ ​q1​(tk​)q2​(tk​)q3​(tk​)q4​(tk​)​ ​
  更新后的旋转矩阵$R_n^b$由与上面公式中更新后的四元数向量的直接关系确定。最后，钻柱的方位角(ψ)、工具面角(ξ)和倾斜角(θ(90°-倾角I))可以用前一节解释的关系推导出来。因此，可以使用以下表达式获得它们: $$\Psi =arctan(\frac{-r_{12}}{r_{22}})$$
$$\xi =arctan(\frac{r_{31}}{r_{33}})$$
$$I=90-\theta =90-arctan(\frac{r_{32}}{\sqrt{r_{12}^2+r_{22}^2}})$$
  下面的步骤更新$t_{k+1}$的速度分量。这可以通过下式来确定沿导航系的钻柱速度变化，如下所示:
$$\Delta V^n(t_{k+1})=R_n^b\Delta v^b-(2{\Omega }_{ie}^n+{\Omega }_{en}^n)V^n\Delta t+g^n\Delta t$$
  最终，更新后的$t_{k+1}$时刻的速度分量$V^n=\left(\begin{array}{ccc}{V}^{east}& V^{north}& V^{up}\end{array}\right)$可用下式得到：
$$V^n(t_{k+1})=V^n(t_k)+\frac{1}{2}(\Delta V^n(t_k)+\Delta V^n(t_{k+1}))$$
  使用修正的欧拉公式计算$t_{k+1}$时钻柱的更新位置(纬度φ、经度λ和真垂直深度h)。h是用方程9中速度矢量垂直分量的关系计算的。表示为:

   在不考虑误差的情况下，利用三轴加速度计和三轴陀螺仪的测量值计算钻柱位置、速度和姿态角的持续更新。然而，由于加速度计和陀螺仪传感器误差和计算误差的综合影响，长期精度会下降。

1.4 钻头合成姿态角

   在静止模式下，根据加速度计测量矢量$f_b$与重力矢量$g^n$之间的关系，仅使用加速度计测量就可以推导出钻头的倾角(90°斜度)和工具面:
f b = ( f x f y f z ) = R n b g n = R n b ( 0 0 − g ) f^b=\begin{pmatrix}f^x\\ f^y\\f^z\end{pmatrix}=R_n^bg^n=R_n^b\begin{pmatrix}0\\ 0\\-g\end{pmatrix} fb= ​fxfyfz​ ​=Rnb​gn=Rnb​ ​00−g​ ​
  其中重力矢量$g^n$由正常重力模型导出。旋转矩阵$R_n^b$将n坐标系中定义的重力向量变换为b坐标系，表示为式1。根据下图的式子，可得到$\theta 、\xi$：

  上式只适用于钻具停止或者钻进速度很慢时。

1.5 基于线性状态方程的测量误差建模

   测量误差必须估计到一定的水平，以达到可接受的系统性能。给定系统的非线性性质，对系统进行摄动，以导出一组线性微分方程。这是使用非线性动态系统的线性化方法完成的。
  可以推导出坐标误差$\left(\begin{array}{ccc}\delta \varphi & \delta \lambda & \delta h\end{array}\right)$、速度误差$\left(\begin{array}{ccc}\delta V^e& \delta V^n& \delta V^u\end{array}\right)$和姿态误差$\left(\begin{array}{ccc}\delta \Psi & \delta \theta & \delta \xi \end{array}\right)$的测量误差。MEMS惯性传感器测量包含偏差和恒定漂移，它们被定义为确定性部分，由校准确定。其余误差被认为是随机的，并被建模为随机过程，其中这些误差随时间相关，并被建模为一阶高斯-马尔可夫(GM)过程或白噪声。在没有外部测量更新的情况下，MEMS惯性传感器的测量误差会随时间漂移。通过应用最优估计工具，如卡尔曼滤波，可以限制这种误差的增长。

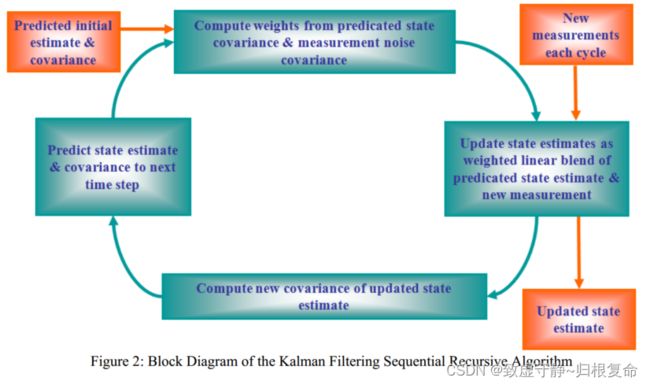
1.6 卡尔曼滤波算法

   卡尔曼滤波是一种计算算法，它通过考虑系统的动力学、系统噪声的特征、测量误差和初始条件信息，推导出系统状态的最小误差估计。将MEMS惯性传感器误差与测量误差相结合，形成$t_k$时刻的误差状态向量${\chi }_k$:
$${\chi }_k=\left(\begin{array}{ccccccccccccccc}\delta \varphi & \delta \lambda & \delta h& \delta V^e& \delta V^n& \delta V^u& \delta \theta & \delta \xi & \delta \Psi & \delta {\omega }_x& \delta {\omega }_y& \delta {\omega }_z& \delta f_x& \delta f_y& \delta f_z\end{array}\right)$$
  最优误差状态最小均方差估计的卡尔曼滤波序贯递推算法如下图所示:

1.7 卡尔曼滤波的钻井观测更新

   如果没有外部观测来更新测量系统，所提出的钻井测量系统将显示出无限增长的位置、速度和姿态误差。两种外部更新方案可以限制MEMS惯性传感器钻孔测量误差的增长。第一种方法是基于连续的钻杆长度测量，可以用来确定钻头的钻进速度。这可以进一步转化为连续速度测量对惯性传感器测量的更新。此外，基于MCM计算的位置应用连续位置。第二种外部更新方案是基于钻井作业定期停止连接新管道时所进行的固定测量。静止更新包括零速度更新(ZUPT)，静止MCM位置更新，以及可用时的磁航向角更新。
  通过卡尔曼滤波算法对MEMS惯性传感器测量和观测更新进行处理，得到测量参数的最优估计，如下图所示。这些观测数据更新的效率取决于这些观测数据的准确性和它们出现的频率。

1.7.1钻井时连续测量观测更新

  通过利用钻杆的长度和时间信息，可以连续地获得钻头的钻进速度。钻杆长度的测量是基于对钻线运动的测量，通过监测转速来记录钻柱的增量增量。这是通过安装的光学编码器来完成的。编码器测量的每英尺脉冲在绘制工程上的每一层都不同。当块被拉起时，通过将每次包裹的脉冲总数校准为相应的深度变化来补偿这一点。只有当钻杆移动时，深度才会增加。当钻柱处于静止状态下进行连接时，深度更新停止。仅依靠钻杆长度和钻井时间来测量钻头的钻速是具有挑战性的。因此，需要替代使用其他独立源。
  从INS得到的速度$\left(\begin{array}{ccc}{V}_{INS}^e& V_{INS}^n& V_{INS}^u\end{array}\right)$与钻头钻速$\left(\begin{array}{ccc}{V}_{update}^e& V_{update}^n& V_{update}^u\end{array}\right)$进行比较。连续的MCM位置$\left(\begin{array}{ccc}{\varphi }_{update}& {\lambda }_{update}& h_{update}\end{array}\right)$是基于一个有效的假设，即两个测量站之间的井眼轨迹位于圆弧上，位置计算基于最小曲率法。根据这些信息，卡尔曼滤波器估计出INS输出中的随机误差。反过来，它通过消除MEMS惯性传感器测量中的估计误差来提高测量系统在钻井时的性能。观测向量$Z_k$表示为:
Z k = ( ϕ I N S − ϕ u p d a t e λ I N S − λ u p d a t e h I N S − h u p d a t e V I N S e − V u p d a t e e V I N S n − V u p d a t e n V I N S u − V u p d a t e u ) Z_k=\begin{pmatrix} \phi_{INS}-\phi_{update} \\ \lambda_{INS}-\lambda_{update} \\ h_{INS}-h_{update}\\ V_{INS}^e-V_{update}^e\\ V_{INS}^n-V_{update}^n\\ V_{INS}^u-V_{update}^u \end{pmatrix} Zk​= ​ϕINS​−ϕupdate​λINS​−λupdate​hINS​−hupdate​VINSe​−Vupdatee​VINSn​−Vupdaten​VINSu​−Vupdateu​​ ​
  表示观测向量$Z_k$与误差状态向量${\chi }_k$之间无噪声关系的设计矩阵$H_k$表示为:
H k = ( ( 1 0 0 0 1 0 0 0 1 ) 0 3 × 3 0 3 × 3 0 3 × 3 0 3 × 3 0 3 × 3 ( 1 0 0 0 1 0 0 0 1 ) 0 3 × 3 0 3 × 3 0 3 × 3 ) H_k=\begin{pmatrix}\begin{pmatrix} 1 & 0&0\\0&1&0\\0&0&1 \end{pmatrix}&0_{3×3}&0_{3×3}&0_{3×3}&0_{3×3}\\ 0_{3×3}&\begin{pmatrix} 1 & 0&0\\0&1&0\\0&0&1 \end{pmatrix}&0_{3×3}&0_{3×3}&0_{3×3} \end{pmatrix} Hk​= ​ ​100​010​001​ ​03×3​​03×3​ ​100​010​001​ ​​03×3​03×3​​03×3​03×3​​03×3​03×3​​ ​
  观测向量$Z_k$和设计矩阵$H_k$的值提供了钻头钻速和MCM位置的卡尔曼滤波测量更新方程:
( ϕ I N S − ϕ u p d a t e λ I N S − λ u p d a t e h I N S − h u p d a t e V I N S e − V u p d a t e e V I N S n − V u p d a t e n V I N S u − V u p d a t e u ) 6 × 1 = ( ( 1 0 0 0 1 0 0 0 1 ) 0 3 × 3 0 3 × 3 0 3 × 3 0 3 × 3 0 3 × 3 ( 1 0 0 0 1 0 0 0 1 ) 0 3 × 3 0 3 × 3 0 3 × 3 ) 6 × 15 ( δ ϕ δ λ δ h δ V e δ V n δ V u δ θ δ ξ δ Ψ δ ω x δ ω y δ ω z δ f x δ f y δ f z ) 15 × 1 + v 6 × 1 \begin{pmatrix} \phi_{INS}-\phi_{update} \\ \lambda_{INS}-\lambda_{update} \\ h_{INS}-h_{update}\\ V_{INS}^e-V_{update}^e\\ V_{INS}^n-V_{update}^n\\ V_{INS}^u-V_{update}^u \end{pmatrix}_{6×1}= \begin{pmatrix} \begin{pmatrix} 1 & 0&0\\0&1&0\\0&0&1 \end{pmatrix}&0_{3×3}&0_{3×3}&0_{3×3}&0_{3×3}\\ 0_{3×3}&\begin{pmatrix} 1 & 0&0\\0&1&0\\0&0&1 \end{pmatrix}&0_{3×3}&0_{3×3}&0_{3×3} \end{pmatrix}_{6×15}\begin{pmatrix} \delta \phi \\ \delta \lambda \\ \delta h \\ \delta V^e\\\delta V^n\\\delta V^u\\ \delta \theta\\\delta \xi\\\delta \Psi\\ \delta \omega_x\\\delta \omega_y\\\delta \omega_z\\ \delta f_x\\\delta f_y\\\delta f_z \end{pmatrix}_{15×1}+v_{6×1} ​ϕINS​−ϕupdate​λINS​−λupdate​hINS​−hupdate​VINSe​−Vupdatee​VINSn​−Vupdaten​VINSu​−Vupdateu​​ ​6×1​= ​ ​100​010​001​ ​03×3​​03×3​ ​100​010​001​ ​​03×3​03×3​​03×3​03×3​​03×3​03×3​​ ​6×15​ ​δϕδλδhδVeδVnδVuδθδξδΨδωx​δωy​δωz​δfx​δfy​δfz​​ ​15×1​+v6×1​

1.7.2 静止测量观测更新

  在大型钻机中，钻井必须每隔30米停止至少5-10分钟，以便连接新的钻杆架。在较小的钻井平台上，为了同样的目的，每隔10米就会停止钻探。在此期间，平稳测量作为观测值更新应用于国际惯性系统。
  第一个平稳更新是零速度更新(ZUPT)。实际上，钻柱是静止的;惯性测量系统的任何速度输出都是加速度计的偏置误差。将这些信息输入到卡尔曼滤波器中，以估计和消除速度误差。观测更新方程的设计矩阵$H_k$如下式所示：
H k = ( 0 3 × 3 ( 1 0 0 0 1 0 0 0 1 ) 0 3 × 3 0 3 × 3 0 3 × 3 ) H_k=\begin{pmatrix} 0_{3×3}&\begin{pmatrix} 1 & 0&0\\0&1&0\\0&0&1 \end{pmatrix}&0_{3×3}&0_{3×3}&0_{3×3} \end{pmatrix} Hk​= ​03×3​​ ​100​010​001​ ​​03×3​​03×3​​03×3​​ ​
   观测向量如下式所示：
Z k = ( V I N S e − V Z U P T e V I N S n − V Z U P T n V I N S u − V Z U P T u ) = ( V I N S e − 0 V I N S n − 0 V I N S u − 0 ) Z_k=\begin{pmatrix} V_{INS}^e-V_{ZUPT}^e\\ V_{INS}^n-V_{ZUPT}^n\\ V_{INS}^u-V_{ZUPT}^u \end{pmatrix}= \begin{pmatrix} V_{INS}^e-0\\ V_{INS}^n-0\\ V_{INS}^u-0 \end{pmatrix} Zk​= ​VINSe​−VZUPTe​VINSn​−VZUPTn​VINSu​−VZUPTu​​ ​= ​VINSe​−0VINSn​−0VINSu​−0​ ​
  钻柱航向观测是在可用的情况下通过磁力计测量获得的。这些测量只在钻柱静止(更新$\Psi$)时提供航向观测。磁航向参考磁北，陀螺仪航向参考真北，因此，磁航向在与陀螺仪得出的航向进行比较之前，必须首先校正为参考真北。这是通过对磁航向进行磁偏角校正来实现的。磁偏角被定义为从真北测得的真北与磁北之间的夹角。其值取决于应用校正的位置和时间;校正可由英国地质调查局全球地磁(BGGM)模型得到。
  参考真北更新${\Psi }_{update}$后的航向观测作为卡尔曼滤波中的直接观测更新来估计惯性衍生航向${\Psi }_{INS}$测量中的随机误差。观测向量$Z_k$与误差状态向量${\chi }_k$之间的关系包含在设计矩阵$H_k$中为:
$$H_k=\left(\begin{array}{ccccccc}{0}_{1\times 3}& 0_{1\times 3}& 0& 0& 1& 0_{1\times 3}& 0_{1\times 3}\end{array}\right)$$
  除了利用航向观测作为直接更新外，它还与固定期间钻柱的倾角一起使用，以类似于连续MCM位置更新的方式计算钻柱的位置坐标。然而，在静止期间，每当钻井停止添加新的管架时，就会计算MCM $\left(\begin{array}{ccc}{\varphi }_{update}& {\lambda }_{update}& h_{update}\end{array}\right)$。表达观测向量$Z_k$与误差状态向量${\chi }_k$关系的设计矩阵$H_k$为:
H k = ( ( 1 0 0 0 1 0 0 0 1 ) 0 3 × 3 0 3 × 3 0 3 × 3 0 3 × 3 ) H_k=\begin{pmatrix} \begin{pmatrix} 1 & 0&0\\0&1&0\\0&0&1 \end{pmatrix}&0_{3×3}&0_{3×3}&0_{3×3}&0_{3×3}\end{pmatrix} Hk​= ​ ​100​010​001​ ​​03×3​​03×3​​03×3​​03×3​​ ​
  卡尔曼滤波器对MEMS惯性传感器测量的随机误差进行估计。这反过来又提高了测量系统在固定时和连接后开始钻井之前的性能。更新时，静止时MCM位置、ZUPT、航向、观测向量$Z_k$、更新表达式如下:
( ϕ I N S − ϕ u p d a t e λ I N S − λ u p d a t e h I N S − h u p d a t e V I N S e − V u p d a t e e V I N S n − V u p d a t e n V I N S u − V u p d a t e u Ψ I N S − Ψ u p d a t e ) 7 × 1 = ( ( 1 0 0 0 1 0 0 0 1 ) 0 3 × 3 0 3 × 3 0 3 × 3 0 3 × 3 0 3 × 3 ( 1 0 0 0 1 0 0 0 1 ) 0 3 × 3 0 3 × 3 0 3 × 3 ( 0 0 0 ) ( 0 0 0 ) ( 0 0 1 ) 0 1 × 3 0 1 × 3 ) 7 × 15 ( δ ϕ δ λ δ h δ V e δ V n δ V u δ θ δ ξ δ Ψ δ ω x δ ω y δ ω z δ f x δ f y δ f z ) 15 × 1 + v 7 × 1 \begin{pmatrix} \phi_{INS}-\phi_{update} \\ \lambda_{INS}-\lambda_{update} \\ h_{INS}-h_{update}\\ V_{INS}^e-V_{update}^e\\ V_{INS}^n-V_{update}^n\\ V_{INS}^u-V_{update}^u\\ \Psi_{INS}-\Psi_{update} \end{pmatrix}_{7×1}= \begin{pmatrix} \begin{pmatrix} 1 & 0&0\\0&1&0\\0&0&1 \end{pmatrix}&0_{3×3}&0_{3×3}&0_{3×3}&0_{3×3}\\ 0_{3×3}&\begin{pmatrix} 1 & 0&0\\0&1&0\\0&0&1 \end{pmatrix}&0_{3×3}&0_{3×3}&0_{3×3}\\ \begin{pmatrix} 0 & 0&0 \end{pmatrix}& \begin{pmatrix} 0 & 0&0 \end{pmatrix}& \begin{pmatrix} 0 & 0&1 \end{pmatrix}&0_{1×3}&0_{1×3} \end{pmatrix}_{7×15}\begin{pmatrix} \delta \phi \\ \delta \lambda \\ \delta h \\ \delta V^e\\\delta V^n\\\delta V^u\\ \delta \theta\\\delta \xi\\\delta \Psi\\ \delta \omega_x\\\delta \omega_y\\\delta \omega_z\\ \delta f_x\\\delta f_y\\\delta f_z \end{pmatrix}_{15×1}+v_{7×1} ​ϕINS​−ϕupdate​λINS​−λupdate​hINS​−hupdate​VINSe​−Vupdatee​VINSn​−Vupdaten​VINSu​−Vupdateu​ΨINS​−Ψupdate​​ ​7×1​= ​ ​100​010​001​ ​03×3​(0​0​0​)​03×3​ ​100​010​001​ ​(0​0​0​)​03×3​03×3​(0​0​1​)​03×3​03×3​01×3​​03×3​03×3​01×3​​ ​7×15​ ​δϕδλδhδVeδVnδVuδθδξδΨδωx​δωy​δωz​δfx​δfy​δfz​​ ​15×1​+v7×1​

1.8 测试结果

二、往期回顾

课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法（基于磁场的测量系统）
课题学习(三)----倾角和方位角的动态测量方法（基于陀螺仪的测量系统）
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法
课题学习(八)----卡尔曼滤波动态求解倾角、方位角
课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记
课题学习(十)----阅读《基于数据融合的近钻头井眼轨迹参数动态测量方法》论文笔记
课题学习(十一)----阅读《Attitude Determination with Magnetometers and Accelerometers to Use in Satellite》
课题学习(十二)----阅读《Extension of a Two-Step Calibration Methodology to Include Nonorthogonal Sensor Axes》
课题学习(十三)----阅读《Calibration of Strapdown Magnetometers in Magnetic Field Domain》论文笔记
课题学习(十四)----三轴加速度计+三轴陀螺仪传感器-ICM20602
课题学习(十五)----阅读《测斜仪旋转姿态测量信号处理方法》论文