带残差连接的ResNet18

目录

1 模型构建

        1.1 残差单元

        1.2 残差网络的整体结构

        2 没有残差连接的ResNet18

        2.1 模型训练

        2.2 模型评价

3 带残差连接的ResNet18

        3.1 模型训练

         3.2 模型评价

4 与高层API实现版本的对比实验

        总结

---

残差网络（Residual Network，ResNet）是在神经网络模型中给非线性层增加直连边的方式来缓解梯度消失问题，从而使训练深度神经网络变得更加容易。

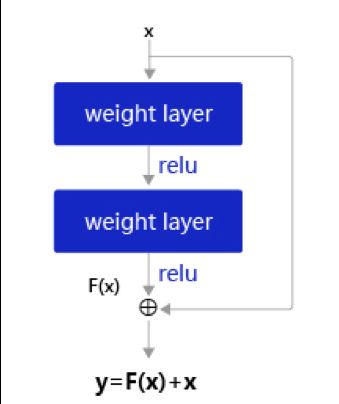
在残差网络中，最基本的单位为残差单元。

假设为一个或多个神经层，残差单元在$f()$的输入和输出之间加上一个直连边。

不同于传统网络结构中让网络去逼近一个目标函数，在残差网络中，将目标函数拆为了两个部分：恒等函数和残差函数

其中为可学习的参数。

一个典型的残差单元如图所示，由多个级联的卷积层和一个跨层的直连边组成。

残差单元结构

 一个残差网络通常有很多个残差单元堆叠而成。下面我们来构建一个在计算机视觉中非常典型的残差网络：ResNet18，并重复上一节中的手写体数字识别任务。

1 模型构建

在本节中，我们先构建ResNet18的残差单元，然后在组建完整的网络。

        1.1 残差单元

这里，我们实现一个算子ResBlock来构建残差单元，其中定义了use_residual参数，用于在后续实验中控制是否使用残差连接。

残差单元包裹的非线性层的输入和输出形状大小应该一致。如果一个卷积层的输入特征图和输出特征图的通道数不一致，则其输出与输入特征图无法直接相加。为了解决上述问题，我们可以使用大小的卷积将输入特征图的通道数映射为与级联卷积输出特征图的一致通道数。

卷积：与标准卷积完全一样，唯一的特殊点在于卷积核的尺寸是，也就是不去考虑输入数据局部信息之间的关系，而把关注点放在不同通道间。通过使用卷积，可以起到如下作用：

•  实现信息的跨通道交互与整合。考虑到卷积运算的输入输出都是3个维度（宽、高、多通道），所以卷积实际上就是对每个像素点，在不同的通道上进行线性组合，从而整合不同通道的信息；
•  对卷积核通道数进行降维和升维，减少参数量。经过卷积后的输出保留了输入数据的原有平面结构，通过调控通道数，从而完成升维或降维的作用；
•  利用卷积后的非线性激活函数，在保持特征图尺寸不变的前提下，大幅增加非线性。

class ResBlock(nn.Module):
    def __init__(self, in_channels, out_channels, stride=1, use_residual=True):

        super(ResBlock, self).__init__()
        self.stride = stride
        self.use_residual = use_residual
        # 第一个卷积层，卷积核大小为3×3，可以设置不同输出通道数以及步长
        self.conv1 = nn.Conv2d(in_channels, out_channels, 3, padding=1, stride=self.stride)
        # 第二个卷积层，卷积核大小为3×3，不改变输入特征图的形状，步长为1
        self.conv2 = nn.Conv2d(out_channels, out_channels, 3, padding=1)

        # 如果conv2的输出和此残差块的输入数据形状不一致，则use_1x1conv = True
        # 当use_1x1conv = True，添加1个1x1的卷积作用在输入数据上，使其形状变成跟conv2一致
        if in_channels != out_channels or stride != 1:
            self.use_1x1conv = True
        else:
            self.use_1x1conv = False
        # 当残差单元包裹的非线性层输入和输出通道数不一致时，需要用1×1卷积调整通道数后再进行相加运算
        if self.use_1x1conv:
            self.shortcut = nn.Conv2d(in_channels, out_channels, 1, stride=self.stride)

        # 每个卷积层后会接一个批量规范化层，批量规范化的内容在7.5.1中会进行详细介绍
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.bn2 = nn.BatchNorm2d(out_channels)
        if self.use_1x1conv:
            self.bn3 = nn.BatchNorm2d(out_channels)

    def forward(self, inputs):
        y = F.relu(self.bn1(self.conv1(inputs)))
        y = self.bn2(self.conv2(y))
        if self.use_residual:
            if self.use_1x1conv:  # 如果为真，对inputs进行1×1卷积，将形状调整成跟conv2的输出y一致
                shortcut = self.shortcut(inputs)
                shortcut = self.bn3(shortcut)
            else:  # 否则直接将inputs和conv2的输出y相加
                shortcut = inputs
            y = torch.add(shortcut, y)
        out = F.relu(y)
        return out

        1.2 残差网络的整体结构

        残差网络就是将很多个残差单元串联起来构成的一个非常深的网络。ResNet18 的网络结构如图所示。

其中为了便于理解，可以将ResNet18网络划分为6个模块：

•  第一模块：包含了一个步长为2，大小为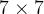的卷积层，卷积层的输出通道数为64，卷积层的输出经过批量归一化、ReLU激活函数的处理后，接了一个步长为2的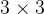的最大汇聚层；
•  第二模块：包含了两个残差单元，经过运算后，输出通道数为64，特征图的尺寸保持不变；
•  第三模块：包含了两个残差单元，经过运算后，输出通道数为128，特征图的尺寸缩小一半；
•  第四模块：包含了两个残差单元，经过运算后，输出通道数为256，特征图的尺寸缩小一半；
•  第五模块：包含了两个残差单元，经过运算后，输出通道数为512，特征图的尺寸缩小一半；
•  第六模块：包含了一个全局平均汇聚层，将特征图变为的大小，最终经过全连接层计算出最后的输出。

ResNet18模型的代码实现如下：

         定义模块一

def make_first_module(in_channels):
    m1 = nn.Sequential(nn.Conv2d(in_channels, 64, 7, stride=2, padding=3), nn.BatchNorm2d(64), nn.ReLU(),
                       nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
    return m1

        定义模块二到模块五

def resnet_module(input_channels, out_channels, num_res_blocks, stride=1, use_residual=True):
    blk = []
    for i in range(num_res_blocks):
        if i == 0:
            blk.append(ResBlock(input_channels, out_channels, stride=stride, use_residual=use_residual))
        else:
            blk.append(ResBlock(out_channels, out_channels, use_residual=use_residual))
    return blk

        封装模块二到模块五

def make_modules(use_residual):
    # 模块二：包含两个残差单元，输入通道数为64，输出通道数为64，步长为1，特征图大小保持不变
    m2 = nn.Sequential(*resnet_module(64, 64, 2, stride=1, use_residual=use_residual))
    # 模块三：包含两个残差单元，输入通道数为64，输出通道数为128，步长为2，特征图大小缩小一半。
    m3 = nn.Sequential(*resnet_module(64, 128, 2, stride=2, use_residual=use_residual))
    # 模块四：包含两个残差单元，输入通道数为128，输出通道数为256，步长为2，特征图大小缩小一半。
    m4 = nn.Sequential(*resnet_module(128, 256, 2, stride=2, use_residual=use_residual))
    # 模块五：包含两个残差单元，输入通道数为256，输出通道数为512，步长为2，特征图大小缩小一半。
    m5 = nn.Sequential(*resnet_module(256, 512, 2, stride=2, use_residual=use_residual))
    return m2, m3, m4, m5

        定义完整网络

class Model_ResNet18(nn.Module):
    def __init__(self, in_channels=3, num_classes=10, use_residual=True):
        super(Model_ResNet18, self).__init__()
        m1 = make_first_module(in_channels)
        m2, m3, m4, m5 = make_modules(use_residual)
        self.net = nn.Sequential(m1, m2, m3, m4, m5, nn.AdaptiveAvgPool2d(1), nn.Flatten(), nn.Linear(512, num_classes))

    def forward(self, x):
        return self.net(x)

        这里同样可以使用torchsummary.summary统计模型的参数量。

from torchsummary import summary

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")  # PyTorch v0.4.0
model = Model_ResNet18(in_channels=1, num_classes=10, use_residual=True).to(device)
summary(model, (1, 32, 32))

         实验结果：

        使用thop.profile统计模型的计算量

from thop import profile

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")  # PyTorch v0.4.0
model = Model_ResNet18(in_channels=1, num_classes=10, use_residual=True).to(device)
dummy_input = torch.randn(1, 1, 32, 32).to(device)

flops, params = profile(model, (dummy_input,))
print(flops)

        为了验证残差连接对深层卷积神经网络的训练可以起到促进作用，接下来先使用ResNet18（use_residual设置为False）进行手写数字识别实验，再添加残差连接（use_residual设置为True），观察实验对比效果。 

        2 没有残差连接的ResNet18

为了验证残差连接的效果，先使用没有残差连接的ResNet18进行实验。

        2.1 模型训练

        使用训练集和验证集进行模型训练，共训练5个epoch。在实验中，保存准确率最高的模型作为最佳模型。代码实现如下

# 固定随机种子
random.seed(0)
# 学习率大小
lr = 0.005
# 批次大小
batch_size = 64
# 加载数据
train_loader = data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = data.DataLoader(dataset=dev_dataset, batch_size=batch_size)
test_loader = data.DataLoader(dataset=test_dataset, batch_size=batch_size)
# 定义网络，不使用残差结构的深层网络
model = Model_ResNet18(in_channels=1, num_classes=10, use_residual=False)
# 定义优化器
optimizer = opt.SGD(lr=lr, params=model.parameters())
# 定义损失函数
loss_fn = F.cross_entropy
# 定义评价指标
metric = Accuracy(is_logist=True)
# 实例化RunnerV3
runner = RunnerV3(model, optimizer, loss_fn, metric)
# 启动训练
log_steps = 15
eval_steps = 15
runner.train(train_loader, dev_loader, num_epochs=5, log_steps=log_steps,
             eval_steps=eval_steps, save_path="best_model.pdparams")
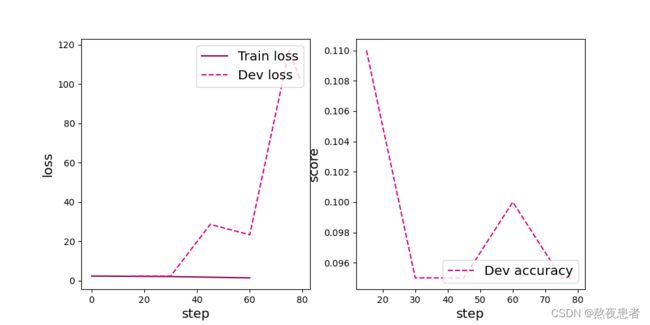
# 可视化观察训练集与验证集的Loss变化情况
plot(runner, 'cnn-loss2.pdf')

 

        2.2 模型评价

        使用测试数据对在训练过程中保存的最佳模型进行评价，观察模型在测试集上的准确率以及损失情况。代码实现如下 

3 带残差连接的ResNet18

        3.1 模型训练

使用带残差连接的ResNet18重复上面的实验，代码实现如下：

random.seed(0)
# 加载 mnist 数据集
train_dataset = MNIST_dataset(dataset=train_set, transforms=transforms, mode='train')
test_dataset = MNIST_dataset(dataset=test_set, transforms=transforms, mode='test')
dev_dataset = MNIST_dataset(dataset=dev_set, transforms=transforms, mode='dev')
# 学习率大小
lr = 0.01
# 批次大小
batch_size = 128
# 加载数据
train_loader = data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = data.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = data.DataLoader(test_dataset, batch_size=batch_size)
# 定义网络，通过指定use_residual为True，使用残差结构的深层网络
model = Model_ResNet18(in_channels=1, num_classes=10, use_residual=True)
# 定义优化器
optimizer = opt.SGD(lr=lr, params=model.parameters())
# 定义损失函数
loss_fn = F.cross_entropy
# 定义评价指标
metric = Accuracy(is_logist=True)
# 实例化RunnerV3
runner = RunnerV3(model, optimizer, loss_fn, metric)
# 启动训练
log_steps = 15
eval_steps = 15
runner.train(train_loader, dev_loader, num_epochs=5, log_steps=log_steps,
             eval_steps=eval_steps, save_path="best_model.pdparams")
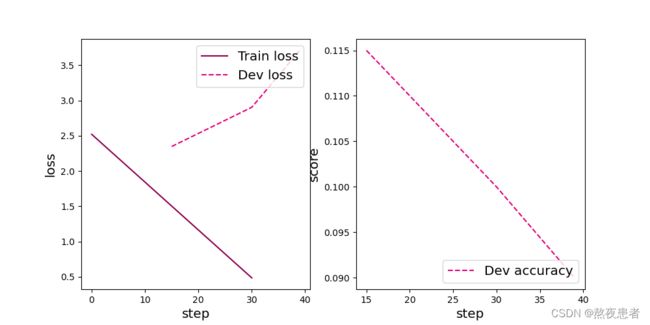
# 可视化观察训练集与验证集的Loss变化情况
plot(runner, 'cnn-loss3.pdf')

         3.2 模型评价

        使用测试数据对在训练过程中保存的最佳模型进行评价，观察模型在测试集上的准确率以及损失情况。

# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))

4 与高层API实现版本的对比实验

对于Reset18这种比较经典的图像分类网络，pytorch中都为大家提供了实现好的版本，大家可以不再从头开始实现。这里为高层API版本的resnet18模型和自定义的resnet18模型赋予相同的权重，并使用相同的输入数据，观察输出结果是否一致。

import torchvision.models as models
from collections import OrderedDict
import warnings

warnings.filterwarnings("ignore")

# 使用飞桨HAPI中实现的resnet18模型，该模型默认输入通道数为3，输出类别数1000
hapi_model = models.resnet18()
# 自定义的resnet18模型
model = Model_ResNet18(in_channels=3, num_classes=1000, use_residual=True)

# 获取网络的权重
params = hapi_model.state_dict()

# 用来保存参数名映射后的网络权重
new_params = {}
# 将参数名进行映射
for key in params:
    if 'layer' in key:
        if 'downsample.0' in key:
            new_params['net.' + key[5:8] + '.shortcut' + key[-7:]] = params[key]
        elif 'downsample.1' in key:
            new_params['net.' + key[5:8] + '.bn3.' + key[22:]] = params[key]
        else:
            new_params['net.' + key[5:]] = params[key]
    elif 'conv1.weight' == key:
        new_params['net.0.0.weight'] = params[key]
    elif 'conv1.bias' == key:
        new_params['net.0.0.bias'] = params[key]
    elif 'bn1' in key:
        new_params['net.0.1' + key[3:]] = params[key]
    elif 'fc' in key:
        new_params['net.7' + key[2:]] = params[key]
    new_params['net.0.0.bias'] = torch.zeros([64])
# 将飞桨HAPI中实现的resnet18模型的权重参数赋予自定义的resnet18模型，保持两者一致
model.load_state_dict(OrderedDict(new_params))

# 这里用np.random创建一个随机数组作为测试数据
inputs = np.random.randn(*[3, 3, 32, 32])
inputs = inputs.astype('float32')
x = torch.tensor(inputs)

output = model(x)
hapi_out = hapi_model(x)

# 计算两个模型输出的差异
diff = output - hapi_out
# 取差异最大的值
max_diff = torch.max(diff)
print(max_diff)

        注意这里代码跑不通显示如下:

Traceback (most recent call last): File "C:\Users\29134\PycharmProjects\pythonProject\DL\实验12\ResNet.py", line 236, in model.load_state_dict(OrderedDict(new_params)) File "C:\ANACONDA\envs\pytorch\Lib\site-packages\torch\nn\modules\module.py", line 2041, in load_state_dict raise RuntimeError('Error(s) in loading state_dict for {}:\n\t{}'.format( RuntimeError: Error(s) in loading state_dict for Model_ResNet18: Missing key(s) in state_dict: "net.0.0.bias", "net.1.0.conv1.bias", "net.1.0.conv2.bias", "net.1.1.conv1.bias", "net.1.1.conv2.bias", "net.2.0.conv1.bias", "net.2.0.conv2.bias", "net.2.0.shortcut.bias", "net.2.1.conv1.bias", "net.2.1.conv2.bias", "net.3.0.conv1.bias", "net.3.0.conv2.bias", "net.3.0.shortcut.bias", "net.3.1.conv1.bias", "net.3.1.conv2.bias", "net.4.0.conv1.bias", "net.4.0.conv2.bias", "net.4.0.shortcut.bias", "net.4.1.conv1.bias", "net.4.1.conv2.bias".

         找了很多资料但是依旧没找到怎么解决，同班同学的代码也跑不通，结论怎么出来的疑惑，这两天时间不太充裕全是结课论文，过两天会回来再次尝试解决这个问题的

        总结

首先，使用带残差连接的ResNet模型相比于不带残差的模型，在训练过程中表现出更好的性能。带残差的模型具有更快的收敛速度、更低的损失和更高的准确率。这证明了残差块确实能够为网络带来性能提升，而无脑堆砌网络层并不能有效地提高模型的性能。这个结果也打破了我一直都认为神经网络越深性能越好的理论认知，同时通过学长的博客我认识到残差连接能够有效地缓解梯度消失问题，减少训练难度，并提高了网络的深度和表达能力。这也算一个小小的收获吧(那一大堆推导我真没看懂！！哭）

放上学长的博客:

NNDL 实验六 卷积神经网络（4）ResNet18实现MNIST-CSDN博客