湖南科技大学计算智能课设（一）基于感知机的鸢尾花分类

基于感知机的鸢尾花分类

写在前面

这篇文章是课设的相关记录，有些地方可能会写的不对，欢迎大家指正。如果我有哪里写的不清楚也可以私信与我沟通，各位写课设的学弟学妹加油～

实验目的

利用感知机算法对鸢尾花种类进行分类，要求熟悉感知机算法，掌握利用Python实现机器学习算法的一般流程，了解 scikit-learn 机器学习库的使用。

背景知识

植物的分类与识别是植物学研究和农林业生产经营中的重要基础工作,对于区分植物种类、探索植物间的亲缘关系、阐明植物系统的进化规律具有重要意义。传统识别植物的方法主要依靠人工，需要丰富的专业知识，工作量大，效率不高，而且难以保证分类的客观性和精确性。随着信息技术飞速发展，将计算机视觉、模式识别、数据库等技术应用于植物种类识别，使得识别更加简单、准确、易行。相对于植物的其它部分，其花朵图像更容易获取，花朵的颜色和形状等都可作为分类依据。本案例在提取花朵形态特征的基础上,利用感知机算法进行分类与识别。
鸢尾花有三个主要类型(种属): tosa 山鸢尾、 Versicolour 变色鸢尾 和 Virginica 维吉尼亚鸢尾，其主要区别是萼片长度、萼片宽度、花瓣长度和花瓣宽度。

鸢尾花数据集：scikit-learn 是基于 Python 的机器学习库，其默认安装包含了几个小型的数据集，并提供了读取这些数据集的接口。 其中 sklearn.datasets.load_iris()用于读取鸢尾花数据集。

感知机（perceptron） 是神经网络的基本组成单元，也被称为神经元，由美国学者 Frank Rosenblatt 于 1957 年提出。下图为一个有三个输入的感知器的结构图。其中 x₁、x₂、x₃ 为输入，w₁、w₂、w₃ 为相应的权值，b 为偏置，f 为激活函数，y 为神经元的输出。偏置 b 也可视为输入恒为1 的边的权值，记为 w₀。

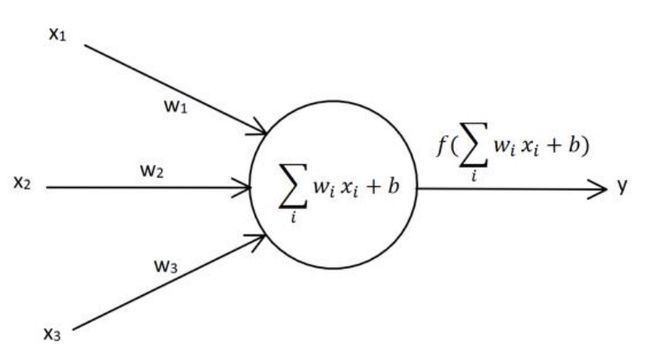
Rosenblatt 在其感知机论文中使用的激活函数是 sign(x)，该函数用来描述一个实数的符号，当 x＞0 时，输出值为 +1；当 x＝ 0 时，输出值为 0；当 x＜0 时，输出值为 -1。

感知器的学习规则，即感知器中的权值参数训练的方法，公式为：$\Delta \mathbf{wi}=\mathbf{lr}(\mathbf{t}-\mathbf{y})\mathbf{xi}$ ，其中 $\Delta \mathbf{wi}$ 表示 第 $\mathbf{i}$ 个权值应该在原基础上变化的值，$\mathbf{lr}$ 表示 学习率(Learning Rate)，用来调节每一次权值变化的速率；$\mathbf{t}$ 是 真值（即目标值target），$\mathbf{y}$ 为神经元的输出，$\mathbf{xi}$ 是 输入。

完整代码

# 加载用到的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris #仅用于加载数据集

iris = load_iris() #加载数据集

## 鸢尾花数据集
# scikit-learn是基于Python的机器学习库，其默认安装包含了几个小型的数据集，并提供了读取这些数据集的接口。
# 其中sklearn.datasets.load_iris()用于读取鸢尾花数据集，该数据集有150组3种类型鸢尾花的4种属性:萼片长度sepal length、萼片宽度sepal width、花瓣长度petal length和花瓣宽度petal width，样本编号与类型的关系是：样本编号0至49为 Setosa ,50至99为 Versicolour ,100至149为 Virginica。

# 通过画图了解三种鸢尾花的分布
# 画图时的中文支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 通过萼片了解三种鸢尾花的分布
plt.figure(dpi=300, figsize=(10,6.5))
plt.clf()
plt.xlim(0, 7)# x轴上的最小值和最大值
plt.ylim(0, 4)
plt.title(u'iris数据集 萼片', fontsize=15)
X=iris.data[:,0:2]

plt.xlabel('petal length 萼片长度', fontsize=13)
plt.ylabel('petal width 萼片宽度', fontsize=13)
plt.plot(X[:50, 0], X[:50, 1], 'o', color='blue', label='Setosa山鸢尾')
plt.plot(X[50:100, 0], X[50:100, 1], 'o', color='orange', label='Versicolour变色鸢尾')
plt.plot(X[100:150, 0], X[100:150, 1], 'o', color='red', label='Virginica维吉尼亚鸢尾')
plt.legend()

plt.show()
plt.pause(3) 
# 从图中大致可以看出，萼片长度和萼片宽度与鸢尾花类型间呈现出非线性关系。

# 通过花瓣了解三种鸢尾花的分布
plt.figure(dpi=300, figsize=(10,6.5))
plt.clf()
plt.xlim(0, 7) # x轴上的最小值和最大值
plt.ylim(0, 3)
plt.title(u'iris数据集 花瓣', fontsize=15)
X=iris.data[:,2:4]

plt.xlabel('petal length 花瓣长度', fontsize=13)
plt.ylabel('petal width 花瓣宽度', fontsize=13)
plt.plot(X[:50, 0], X[:50, 1], 'o', color='blue', label='Setosa山鸢尾')
plt.plot(X[50:100, 0], X[50:100, 1], 'o', color='orange', label='Versicolour变色鸢尾')
plt.plot(X[100:150, 0], X[100:150, 1], 'o', color='red', label='Virginica维吉尼亚鸢尾')
plt.legend()

plt.show()
plt.pause(3) 
# 从图中大致可以看出，花瓣长度和花瓣宽度与鸢尾花类型间有较好的线性关系，使用花瓣数据来划分鸢尾花类型效果更好。

## 算法初始化
X=np.c_[np.ones(100),iris.data[:100,2:4]] # 输入 X（偏置+两个特征） 100*3
T=iris.target[:100].reshape(100,1) # 得到真值T，从数据集中得到真值（目标值） 100*1
T[T!=1] = -1 # 将T中所有不等于1的元素赋值为-1，以契合sign函数
W = np.array([[1], # 权值初始化，3行1列，即w0 w1 w2  
              [1],
              [1]])
lr = 1 # 学习率设置
Y = 0 # 神经网络输出

## 学习算法
# 训练感知机模型
# 更新一次权值
def train():
    global W # 使用全局变量W（权值）
    Y = np.sign(np.dot(X,W)) # 同时计算100个数据的预测值，Y的形状为(100,1)-100行1列，输出=权值(W)*输入(X) 100*3 * 3*1 = 100*1
    E = T - Y # T - Y得到100个的标签值与预测值的误差E，形状为(100,1)，T是目标值，E是目标值-输出 100*1
    # X的形状为(100,3)
    # X.T表示X的转置矩阵，形状为(3,100)
    # 我们一共有100个数据，每个数据3个特征的值。定义第i个数据的第j个特征值为xij
    # 如第1个数据，第2个值为x12
    # X.T.dot(E)为一个3行1列的数据：
    # 第1行等于：x0_0×e0+x1_0×e1+x2_0×e2+x3_0×e3+...+x99_0×e99，它会调整权值W0
    # 第2行等于：x0_1×e0+x1_1×e1+x2_1×e2+x3_1×e3+...+x99_1×e99，它会调整权值W1
    # 第3行等于：x0_2×e0+x1_2×e1+x2_2×e2+x3_2×e3+...+x99_2×e99，它会调整权值W2
    # X.shape表示X的形状X.shape[0]得到X的行数，表示有多少个数据
    # X.shape[1]得到列数，表示每个数据有多少个特征值。
    delta_W = lr * (X.T.dot(E)) / X.shape[0] # 学习率*（x转制*E）/ 100 即 = ( − )
    W = W + delta_W # 更新权值

## 画图函数
def draw():
    plt.clf()
    plt.xlim(0, 6)#x轴上的最小值和最大值
    plt.ylim(0, 2)#y轴上的最小值和最大值
    plt.title(u'Perceptron感知器 epoch:%d\n W0:%f W1:%f W2:%f' %(i+1,W[0],W[1],W[2]), fontsize=15)
       
    plt.xlabel('petal length 花瓣长度', fontsize=13)
    plt.ylabel('petal width 花瓣宽度', fontsize=13)
    # 用红色的点来画出正样本
    plt.plot(X[:50, 1], X[:50, 2], 'o', color='red', label='Setosa山鸢尾')
    # 用蓝色的点来画出负样本
    plt.plot(X[50:100, 1], X[50:100, 2], 'o', color='blue', label='Versicolour变色鸢尾')
    plt.plot(2.5, 1, '+', color='black', label='待预测点')
    
    k = - W[1] / W[2]
    d =  -W[0] / W[2]
    # 设定两个点
    xdata = (0,6)
    # 通过两个点来确定一条直线，用黑色的线来画出分界线
    plt.plot(xdata,xdata * k + d,'black', linewidth=3)
    plt.legend()
    ######################################################以下绘制决策面两边的颜色，不要求掌握
    # 生成决策面 
    from matplotlib.colors import ListedColormap #绘制决策面两边的颜色，不要求掌握
    # 生成x,y的数据
    n = 256
    xx = np.linspace(0, 6, n)
    yy = np.linspace(0, 2, n)
    # 把x,y数据生成mesh网格状的数据，因为等高线的显示是在网格的基础上添加上高度值
    XX, YY = np.meshgrid(xx, yy)
    # 填充等高线
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')  
    cmap = ListedColormap(colors[:len(np.unique(np.sign(W[0]+W[1]*XX+W[2]*YY)))])  
    plt.contourf(XX, YY, np.sign(W[0]+W[1]*XX+W[2]*YY),8, alpha = 0.5, cmap=cmap)
    #######################################################以上绘制决策面两边的颜色，不要求掌握
    plt.pause(0.1)
    plt.show()

## 训练1000次
for i in range(1000):
    if(i==0):    #特地画出未经训练的初始图像，以方便理解
        draw()
        plt.pause(5)  #停留两秒，这是分类直线最初的位置，取决于W的初始值，是人为决定的超参数
    train()      #更新一次权值
    draw()       #画出更新一次权值后的图像
    Y = np.sign(np.dot(X,W)) 
    # .all()表示Y中的所有值跟T中所有值都对应相等，结果才为真
    if(Y == T).all(): 
        print('Finished')
        # 跳出循环
        break

代码讲解

1）加载用到的库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris #仅用于加载数据集

2）加载鸢尾花数据集

iris = load_iris()

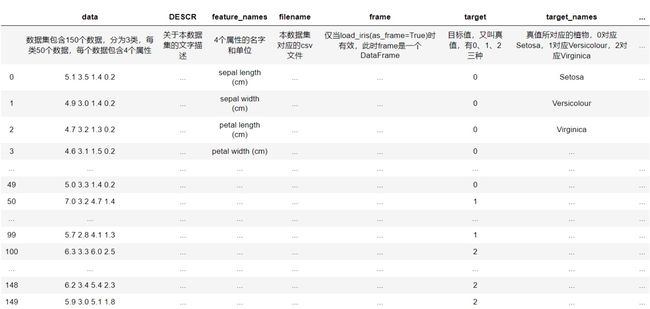
scikit-learn 提供了读取鸢尾花数据集的接口 sklearn.datasets.load_iris()，该数据集有 150 组 3 种类型鸢尾花的 4 种属性：萼片长度 sepal length、萼片宽度 sepal width、花瓣长度 petal length 和花瓣宽度 petal width，样本编号与类型的关系是：样本编号 0 至 49 为 Setosa ,50 至 99 为Versicolour ,100 至 149 为 Virginica。
代码 iris = load_iris()中得到的 iris 是一个字典，包含七个 “key-value” 对：

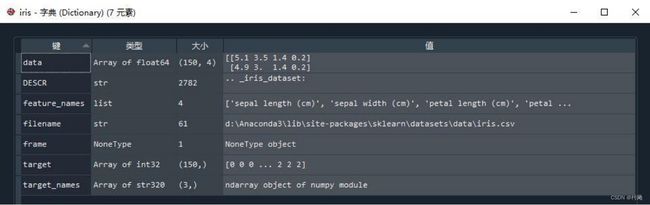
其中每一个 key 的意义和 value 说明如下：

3）通过画图了解三种鸢尾花的分布

# 画图时的中文支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 通过萼片了解三种鸢尾花的分布

plt.clf()
plt.xlim(0, 7)#x轴上的最小值和最大值
plt.ylim(0, 4)
plt.title(u'iris数据集 萼片', fontsize=15)
X=iris.data[:,0:2]

plt.xlabel('petal length 萼片长度', fontsize=13)
plt.ylabel('petal width 萼片宽度', fontsize=13)
plt.plot(X[:50, 0], X[:50, 1], 'o', color='blue', label='Setosa山鸢尾')
plt.plot(X[50:100, 0], X[50:100, 1], 'o', color='orange', label='Versicolour变色鸢尾')
plt.plot(X[100:150, 0], X[100:150, 1], 'o', color='red', label='Virginica维吉尼亚鸢尾')
plt.legend()

plt.show()
plt.pause(3) 

从图中大致可以看出，萼片长度和萼片宽度与鸢尾花类型间呈现出非线性关系。

# 通过花瓣了解三种鸢尾花的分布

plt.clf()
plt.xlim(0, 7)#x轴上的最小值和最大值
plt.ylim(0, 3)
plt.title(u'iris数据集 花瓣', fontsize=15)
X=iris.data[:,2:4]

plt.xlabel('petal length 花瓣长度', fontsize=13)
plt.ylabel('petal width 花瓣宽度', fontsize=13)
plt.plot(X[:50, 0], X[:50, 1], 'o', color='blue', label='Setosa山鸢尾')
plt.plot(X[50:100, 0], X[50:100, 1], 'o', color='orange', label='Versicolour变色鸢尾')
plt.plot(X[100:150, 0], X[100:150, 1], 'o', color='red', label='Virginica维吉尼亚鸢尾')
plt.legend()

plt.show()
plt.pause(3) 

从图中大致可以看出，花瓣长度和花瓣宽度与鸢尾花类型间有较好的线性关系，使用花瓣数据来划分鸢尾花类型效果更好。

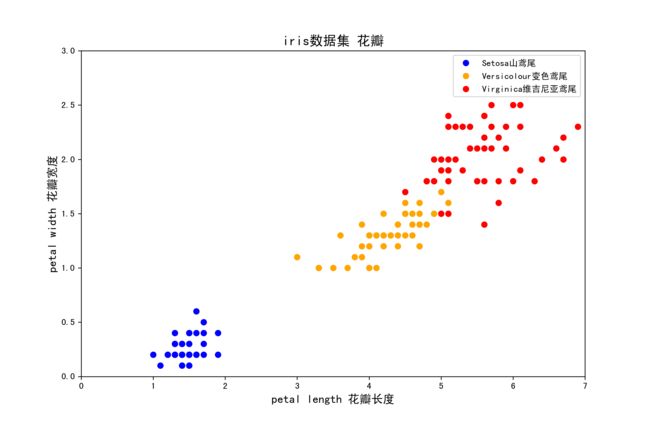
4）算法初始化

X=np.c_[np.ones(100),iris.data[:100,2:4]] # 输入 X（偏置+两个特征） 100*3
T=iris.target[:100].reshape(100,1) # 得到真值T，从数据集中得到真值（目标值） 100*1
T[T!=1] = -1 # 将T中所有不等于1的元素赋值为-1，以契合sign函数  
W = np.array([[1], # 权值初始化，3行1列，即w0 w1 w2
              [1],
              [1]])
lr = 1 # 学习率设置
Y = 0 # 神经网络输出

np.ones(100) 生成 100 行 1 列的 1，作为偏置的输入。
iris.data[:100,2:4] 得到前 100 行, 第 2 列和第 3 列的数据，作为两个特征(花瓣长度、花瓣宽度)的输入。
np.c_ 是 按行 连接两个矩阵，就是把两矩阵左右相连形成一个新矩阵，要求行数相等。
组合两个特征和偏置，形成最终的输入 X。
X=(x₀ x₁ x₂)，即偏置、花瓣长度、花瓣宽度。
真值 T 直接从数据集中得到，然后将 T 中所有不等于 1 的元素赋值为 -1，以契合接下来将要使用到的 sign 函数。

5）学习算法

# 训练感知机模型
# 更新一次权值
def train():
    global W # 使用全局变量W(权值)
    Y = np.sign(np.dot(X,W)) # 同时计算100个数据的预测值,Y的形状为(100,1)-100行1列,输出=权值(W)*输入(X) 100*3 * 3*1 = 100*1
    E = T - Y # T - Y 得到100个的标签值与预测值的误差E,形状为(100,1),T是目标值,E是目标值-输出 100*1
    # X的形状为(100,3)
    # X.T表示X的转置矩阵，形状为(3,100)
    # 我们一共有100个数据，每个数据3个特征的值。定义第i个数据的第j个特征值为xi_j
    # 如第1个数据，第2个特征值为x1_2
    # X.T.dot(E)为一个3行1列的数据：
    # 第1行等于：x0_0×e0+x1_0×e1+x2_0×e2+x3_0×e3+...+x99_0×e99，它会调整权值W0
    # 第2行等于：x0_1×e0+x1_1×e1+x2_1×e2+x3_1×e3+...+x99_1×e99，它会调整权值W1
    # 第3行等于：x0_2×e0+x1_2×e1+x2_2×e2+x3_2×e3+...+x99_2×e99，它会调整权值W2
    # X.shape表示X的形状X.shape[0]得到X的行数，表示有多少个数据
    # X.shape[1]得到列数，表示每个数据有多少个特征值。
    delta_W = lr * (X.T.dot(E)) / X.shape[0] # 学习率*（x转制*E）/ 100 即 = ( − )
    W = W + delta_W # 更新权值

6）画图函数

def draw():
    plt.clf()
    plt.xlim(0, 6)#x轴上的最小值和最大值
    plt.ylim(0, 2)#y轴上的最小值和最大值
    plt.title(u'Perceptron感知器 epoch:%d\n W0:%f W1:%f W2:%f' %(i+1,W[0],W[1],W[2]), fontsize=15)
       
    plt.xlabel('petal length 花瓣长度', fontsize=13)
    plt.ylabel('petal width 花瓣宽度', fontsize=13)
    # 用红色的点来画出正样本
    plt.plot(X[:50, 1], X[:50, 2], 'o', color='red', label='Setosa山鸢尾')
    # 用蓝色的点来画出负样本
    plt.plot(X[50:100, 1], X[50:100, 2], 'o', color='blue', label='Versicolour变色鸢尾')
    plt.plot(2.5, 1, '+', color='black', label='待预测点')
    
    k = - W[1] / W[2]
    d =  -W[0] / W[2]
    # 设定两个点
    xdata = (0,6)
    # 通过两个点来确定一条直线，用黑色的线来画出分界线
    plt.plot(xdata,xdata * k + d,'black', linewidth=3)
    plt.legend()
    ######################################################以下绘制决策面两边的颜色，不要求掌握
    # 生成决策面 
    from matplotlib.colors import ListedColormap #绘制决策面两边的颜色，不要求掌握
    # 生成x,y的数据
    n = 256
    xx = np.linspace(0, 6, n)
    yy = np.linspace(0, 2, n)
    # 把x,y数据生成mesh网格状的数据，因为等高线的显示是在网格的基础上添加上高度值
    XX, YY = np.meshgrid(xx, yy)
    # 填充等高线
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')  
    cmap = ListedColormap(colors[:len(np.unique(np.sign(W[0]+W[1]*XX+W[2]*YY)))])  
    plt.contourf(XX, YY, np.sign(W[0]+W[1]*XX+W[2]*YY),8, alpha = 0.5, cmap=cmap)
    #######################################################以上绘制决策面两边的颜色，不要求掌握
    plt.pause(0.1)
    plt.show()

7）主函数

## 训练1000次
for i in range(1000):
    if(i==0):    #特地画出未经训练的初始图像，以方便理解
        draw()
        plt.pause(5)  #停留两秒，这是分类直线最初的位置，取决于W的初始值，是人为决定的超参数
    train()      #更新一次权值
    draw()       #画出更新一次权值后的图像
    Y = np.sign(np.dot(X,W)) 
    # .all()表示Y中的所有值跟T中所有值都对应相等，结果才为真
    if(Y == T).all(): 
        print('Finished')
        # 跳出循环
        break

实验内容

1）考虑学习率的作用。修改示例代码，固定初始权值=(1,1,1)，将学习率分别设定为 1、0.5、0.1（组合 1~3），程序在 epoch 等于多少时实现分类？

这道题就是在“算法初始化”部分将lr这个参数修改成题目中的值，将w改成(1,1,1)后固定不变，然后分别运行一遍，epoch就是将最后运行出来的i的值+1（i是主函数里的），epoch也可以通过观察运行完后的最后一张图的右上方（标题右边）来获得，但是当权值更新次数太多时有可能会出现图片无法全部显示的情况，也就是说这种情况下你是看不到最后一张图片的（pycharm可能会出现这种情况）。

组合1:

W = np.array([[1], # 权值初始化，3行1列，即w0 w1 w2  
              [1],
              [1]])
lr = 1 # 学习率设置

组合2:

W = np.array([[1], # 权值初始化，3行1列，即w0 w1 w2  
              [1],
              [1]])
lr = 0.5 # 学习率设置

组合3:

W = np.array([[1], # 权值初始化，3行1列，即w0 w1 w2  
              [1],
              [1]])
lr = 0.1 # 学习率设置

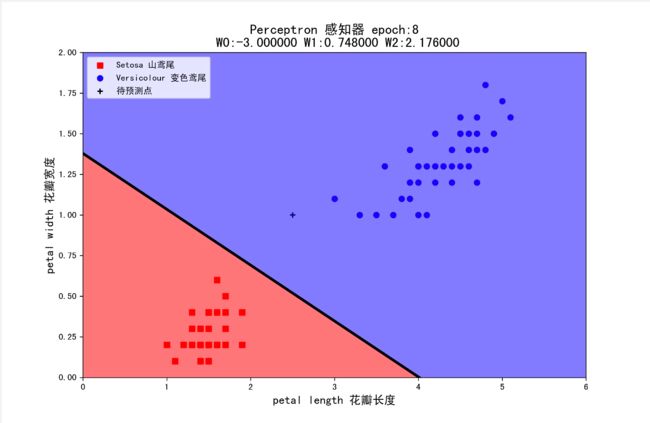
当学习率为 1 时，epoch 等于 8 时实现分类；
当学习率为 0.5 时，epoch 等于 9 时实现分类；
当学习率为 0.1 时，epoch 等于 181 时实现分类。
2）考虑初始权值的作用。修改示例代码，固定学习率=0.1，将初始权值分别设定为(-1,1,1)、 (+1,-1,-1)、(1,-1,+1) 、(-1,+1,-1) （组合 4~7），程序在 epoch 等于多少时实现分类？

这道题就是在“算法初始化“部分将w这个参数修改成题目中的值，将lr改成0.1后固定不变，然后分别运行一遍，epoch的获取方法与上题一致。

组合4:

W = np.array([[-1], # 权值初始化，3行1列，即w0 w1 w2  
              [1],
              [1]])
lr = 0.1 # 学习率设置

组合5:

W = np.array([[1], # 权值初始化，3行1列，即w0 w1 w2  
              [-1],
              [-1]])
lr = 0.1 # 学习率设置

其余组合就也按照这个方法改就行。

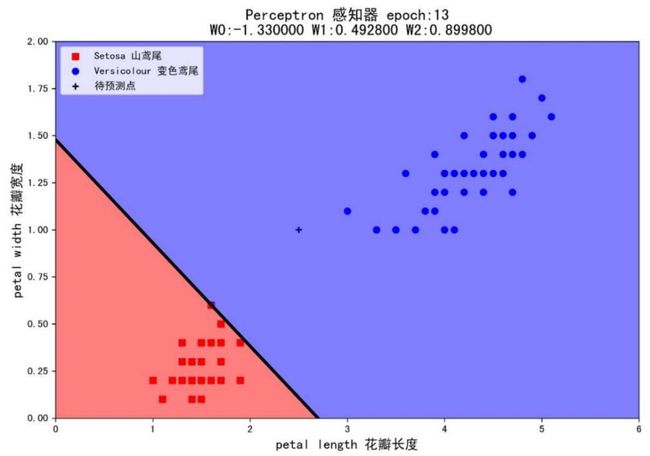
当初始权值为(-1,1,1)时，epoch 等于 13 时实现分类；
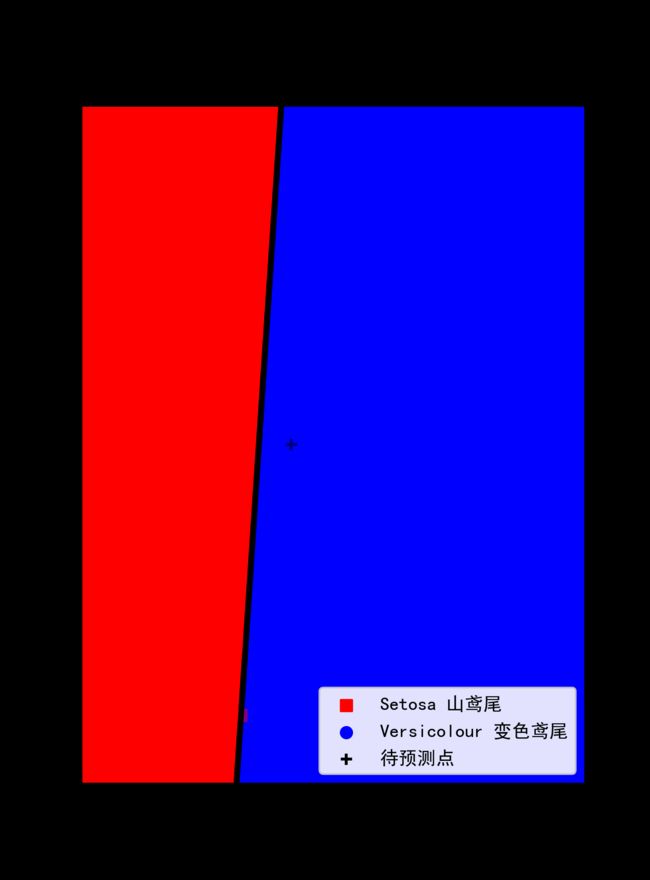
当初始权值为(+1,-1,-1)时，epoch 等于 33 时实现分类；
当初始权值为(1,-1,+1)时，epoch 等于 324 时实现分类；
当初始权值为(-1,+1,-1)时，epoch 等于 144 时实现分类。
3）示例程序使用的是离散感知机还是连续感知机？如何判断？
离散感知机和连续感知机根据激活函数是否连续来分类，激活函数离散则对应的感知器是离散感知器；激活函数连续则对应的感知器是连续感知器。连续单输出感知器的输出不是离散的值，而是连续的值。用公式 w = w + α (y - o) x 取代了上述离散单输出感知器算法中的 W = W + eX 。这样 y 与 o 之间的差别对 W 的影响由 α (y - o) x 表现出来，其中 α 为学习率。 本程序中使用的激活函数 sign 函数是连续的，并且目标值与输出之间的差别对权值的影响用 ∆wi = lr (t − y) xi来表现，所以本程序使用的感知机是连续的。
4）为什么在学习算法中要除以 X.shape[0] ？示例程序采用的是批量下降还是逐一下降？是否属于随机下降？是否属于梯度下降？
因为 lr * (X.T.dot(E)) 计算的是 100 个样本总共的∆wi = lr (t − y) xi，X.shape[0]代表样本个数，除以 X.shape[0]以取平均值，来作为本次计算出来的∆wi。
示例程序采用的是批量下降，因为在更新参数时，程序使用所有的样本来进行更新。
不属于随机下降。
属于梯度下降，梯度下降是连续感知机所使用的学习方法。
5）假设你在自然界找到了一朵鸢尾花，并测得它的花瓣长度为 2.5cm，花瓣宽度为 1cm，它属于哪一类？在 draw()中已用 plt.plot 画出这个‘待预测点’。请观察 1~7 这 7 种组合中，感知机的判断始终一致么？这说明它受到什么因素的影响？
由官方给出的数据画出的散点图可得，该鸢尾花可能属于山鸢尾，也可能属于变色鸢尾，属于后者的概率更大。

组合 1(lr=1,W=(1,1,1)):判断该花为变色鸢尾

组合 2(lr=0.5,W=(1,1,1)):判断该花为变色鸢尾

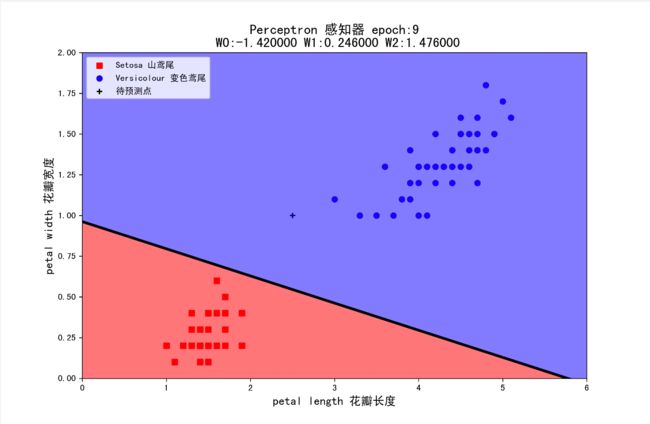
组合 3(lr=0.1,W=(1,1,1)):判断该花为变色鸢尾

组合 4(lr=0.1,W=(-1,1,1)):判断该花为变色鸢尾

组合 5(lr=0.1,W=(1,-1,-1)):判断该花为变色鸢尾

组合 6(lr=0.1,W=(1,-1,1)):判断该花为变色鸢尾

组合 7(lr=0.1,W=(-1,1,-1)):判断该花为山鸢尾

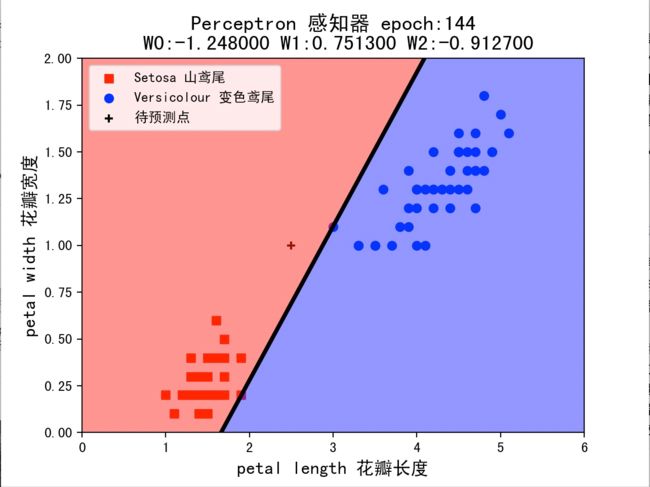
这 7 种组合中，组合 7 的判断与其余组不一致，花类别的判断可能受到初始权值的影响。
6）修改示例代码，将变色鸢尾的数据替换为维吉尼亚鸢尾，再进行分类。即横轴为花瓣长度，纵轴为花瓣宽度，数据为 Setosa 山鸢尾+ Virginica 维吉尼亚鸢尾。
将算法初始化部分的输入（X）和目标值（T）换成 Setosa 山鸢尾 + Virginica 维吉尼亚鸢尾的数据，其余部分不变，变动部分代码如下：

数据集中样本编号 0 至 49 为 Setosa ,50 至 99 为 Versicolour ,100 至 149 为 Virginica，所以要提取 Setosa 山鸢尾 + Virginica 维吉尼亚鸢尾的数据的话就是把0～49和100～149的部分拼接起来，data当作输入值X，target当作目标值T，因为原始数据集中 Virginica 维吉尼亚鸢尾的目标值是2， Setosa 山鸢尾的目标值是0，所以为了契合 sign 函数，就将为2的值改成了1，为0的值改成了 -1（问就是 sign 算出来的数只能是1或 -1，所以为了让代码通过调整后的权值来计算出来的输出与数据集中的目标值一致，所以原数据集中的目标值需要改值）。那为啥是 Virginica 维吉尼亚鸢尾的目标值改为1，而不是 Setosa 山鸢尾的目标值改为1捏，主要是因为权值与输入相乘后实际得到的值 Virginica 维吉尼亚鸢尾的输出都是正数，而 Setosa 山鸢尾的输出都是负数，所以为了顺应 sign 函数”取符号“这一点，就这样改了（注意这里必须这么改，不能调换过来）。np.vstack 是 按列 连接两个矩阵，就是把两矩阵上下拼接形成一个新矩阵，要求列数相等。

X=np.c_[np.ones(100),np.vstack((iris.data[:50,2:4],iris.data[100:150,2:4]))] #输入 X（偏置+两个特征） 100*3
T=np.vstack((iris.target[:50],iris.target[100:150])).reshape(100,1) #目标值 T 100*1
T[T==2] = 1 #将 2 用 1 表示，以契合 sign 函数
T[T==0] = -1 #将 0 用 -1 表示，以契合 sign 函数

以下是将组合1～7全都跑了一遍得出的结果：
组合1:学习率为1，初始权值为(1,1,1)

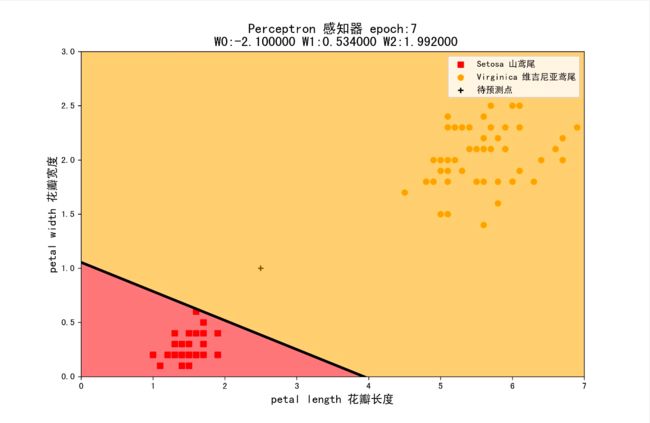
组合2:学习率为0.5，初始权值为(1,1,1)

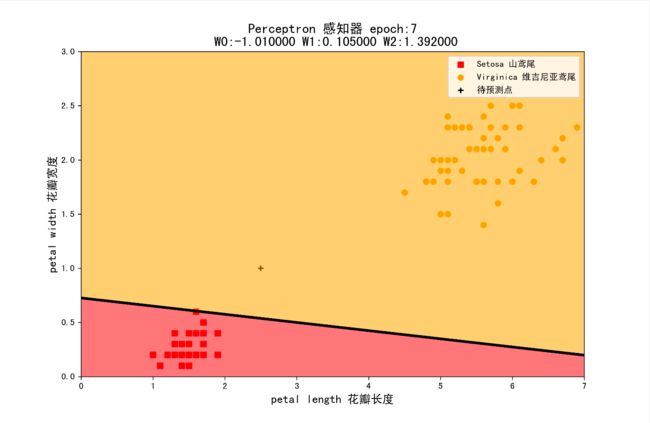
组合3:学习率为0.1，初始权值为(1,1,1)

组合4:学习率为0.1，初始权值为(-1,1,1)

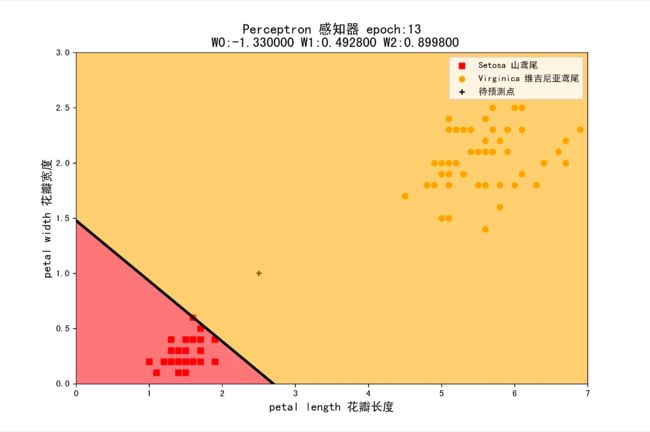
组合5:学习率为0.1，初始权值为(1,-1,-1)

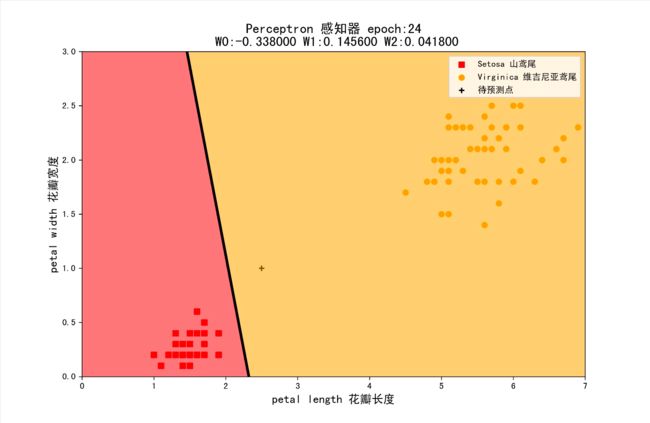
组合6:学习率为0.1，初始权值为(1,-1,1)

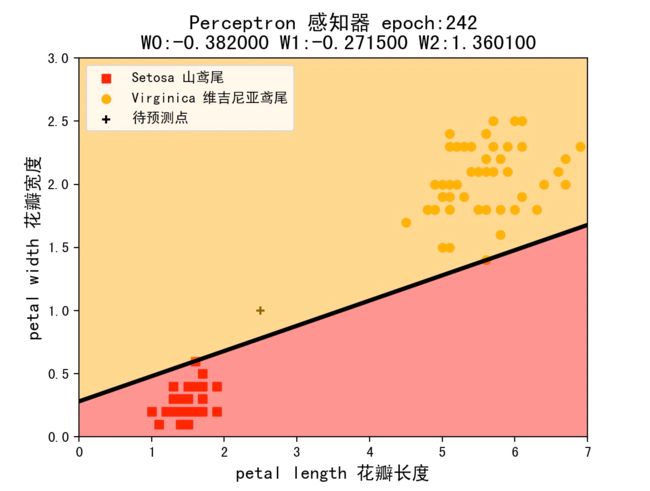
组合7:学习率为0.1，初始权值为(-1,1,-1)

7）【可选】目前感知机只有两个输入+偏置，如果有三个输入（比如增加萼片长度作为输入），程序应如何修改（可以不画图）？
这道题我是在上一题的基础上用 Setosa 山鸢尾和 Virginica 维吉尼亚鸢尾的数据做的，所以是在上一题的代码上继续修改的。只修改了算法初始化部分，其余部分不变。考虑到萼片长度在 Setosa 山鸢尾和 Virginica 维吉尼亚鸢尾两种类型中相差不大，不能很好地作为分类依据，所以将其做平方处理，以拉大两种类型中数字的差距。将偏置+三个特征拼成100行4列的数据，作为输出。目标值为了与 sign 函数契合，将值为2的变为1，值为0的变为 -1。将权值设为 (1,1,1,1)，学习率设为0.1，开始训练数据集。np.r_ 是 按列 连接两个矩阵，就是把两矩阵上下拼接形成一个新矩阵，要求列数相等。
改动的代码如下：

a1=np.r_[iris.data[:50,2:4],iris.data[100:150,2:4]] # 取Setosa山鸢尾和Virginica维吉尼亚鸢尾的花瓣长度、花瓣宽度上下拼接
a2=np.r_[iris.data[:50,0],iris.data[100:150,0]] # 取Setosa山鸢尾和Virginica维吉尼亚鸢尾的萼片长度上下拼接
a2=a2*a2 # 将萼片长度这一数据平方
a=np.c_[a1,a2] # 将Setosa山鸢尾和Virginica维吉尼亚鸢尾的花瓣长度、花瓣宽度、萼片长度三个特征左右拼接 100*3
X=np.c_[np.ones(100),a] # 输入 X（偏置+三个特征） 100*4
T=np.vstack((iris.target[:50],iris.target[100:150])).reshape(100,1) # 目标值 T 100*1
T[T==2] = 1 # 将 2 用 1 表示，以契合 sign 函数
T[T==0] = -1 # 将 0 用 -1 表示，以契合 sign 函数
W = np.array([[1], # 权值初始化，4 行 1 列，即 w0 w1 w2 w4 4*1
              [1],
              [1],
              [1]])
lr = 0.1 # 学习率设置
Y = 0 # 神经网络输出

当epoch为40，权值更新为 (-0.12, 5.0386, 3.1726, -0.4785) 时，数据可以进行很好地分类。
所得结果如下：
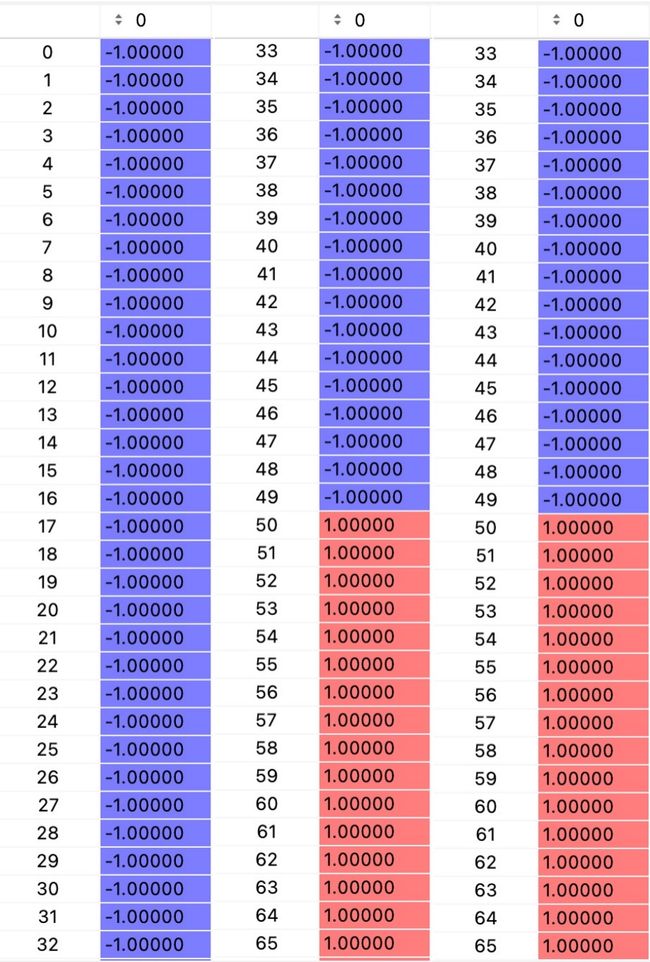
输入x权重（np.dot(X,W)）:

输出（Y）：

目标值（T）：

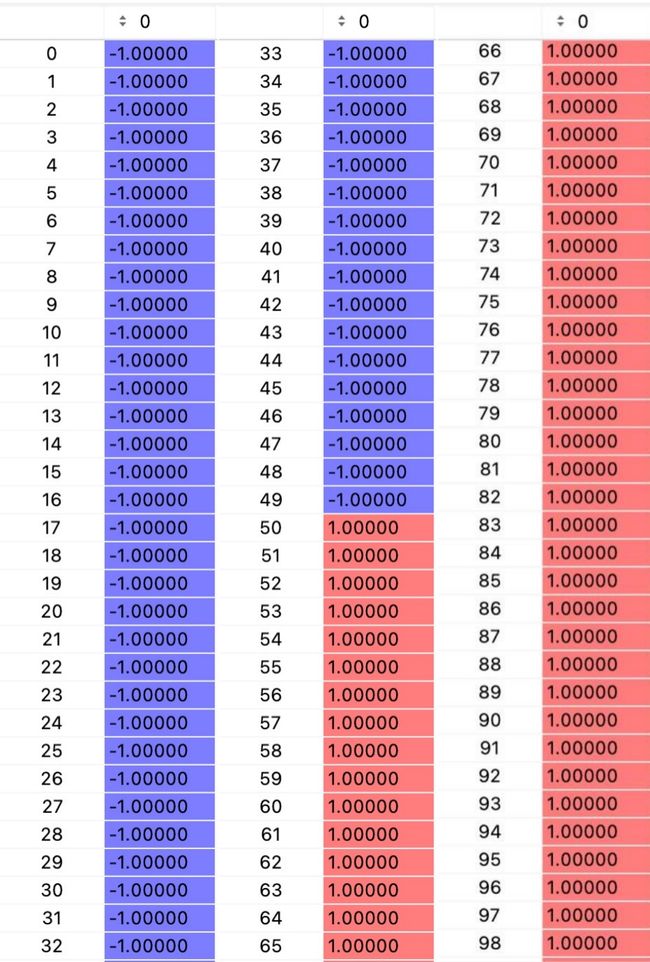
如图所示，可以准确的分类已知数据集（输出与目标值都对上了）。

实验结果与分析

感知机可以很好地用来对数据集进行分类，其中学习率和初始权重对分类所用时间和分类结果产生着一定的影响。
由1）、5）、6）小题可知，学习率主要对分类所用时间，即迭代次数epoch影响较大，学习率越大代表每次搜索正确答案时所迈的步子越大，所以其迭代次数epoch越小。由5）、6）题的前三组所画出的最后结果实验图可知，当学习率为0.1时，最后划分种类的分割线的位置发生了较大的改变，但最后划分的结果没有变，说明学习率可能也对结果产生着影响，只是比较微小的影响。在第5）题中当学习率为0.1时，其分类效果也不太好，存在着边界点分不开的情况。
由2）、5）、6）小题可知，初始权重对迭代次数和分类结果都有着较大的影响。当初始权重下对训练集的分类结果与最终分类结果差别较大时，往往可能造成迭代次数的增加或测试集分类结果不准确。
由6）、7）小题可知，当增加了一个特征时，可能对迭代次数和分类结果有正向的影响，6）题lr=0.1，W=（1，1，1）时，epoch=129，7）题lr=0.1，W=（1，1，1）时，epoch=40，对减少迭代次数有比较显著的影响。

实验小结

这个实验整体不难，想要看懂代码首先要理解感知机的运算逻辑即权重更新的那个公式，还要清楚每一步运算的矩阵的维度，这样才能清楚每一行代码都是干什么的。