湖南科技大学计算智能课设（四）遗传算法求解无约束单目标优化问题

遗传算法求解无约束单目标优化问题

写在前面

这篇文章是课设的相关记录，有些地方可能会写的不对，欢迎大家指正。如果我有哪里写的不清楚也可以私信与我沟通，各位写课设的学弟学妹加油～

实验目的

理解遗传算法原理，掌握遗传算法的基本求解步骤，包括选择、交叉、变异等，学会运用遗传算法求解无约束单目标优化问题。

背景知识

遗传算法(Genetic Algorithm)是借鉴生物界自然选择、适者生存遗传机制的一种随机搜索方法。
遗传算法模拟了进化生物学中的遗传、突变、自然选择以及杂交等现象，是进化算法的一种。对于一个最优化问题，一定数量的候选解（每个候选解称为一个个体）的抽象表示（也称为染色体）的种群向更好的方向解进化，通过一代一代不断繁衍，使种群收敛于最适应的环境，从而求得问题的最优解。进化从完全随机选择的个体种群开始，一代一代繁殖、进化。在每一代中，整个种群的每个个体的适应度被评价，从当前种群中随机地选择多个个体（基于它们的适应度），通过自然选择、优胜劣汰和突变产生新的种群，该种群在算法的下一次迭代中成为当前种群。传统上，解一般用二进制表示（0 和 1 组成的串）。
遗传算法的主要特点是直接对结构对象进行操作，不存在函数求导、连续、单峰的限定；具有内在的隐闭并行性和更好的全局寻优能力；采用概率化的寻优方法，能自动获取和指导优化搜索，自适应调整搜索方向，不需要确定的规则。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工智能等领域中的问题求解，已成为现代智能计算中的一项关键技术。
关键术语：
(1)个体( individuals)：遗传算法中所处理的对象称为个体。个体通常可以含解的编码表示形式、适应度值等构成成分，因而可看成是一个结构整体。其中，主要成分是编码。
(2)种群(population)：由个体构成的集合称为种群。
(3)位串(bit string)：解的编码表示形式称为位串。解的编码表示可以是 0、1 二值串、0~9 十进制数字串或其他形式的串，可称为字符串或简称为串。位串和染色体(chromosome)相对应。在遗传算法的描述中，经常不加区分地使用位串和染色体这两个概念。位串/染色体与个体的关系：位串/染色体一般是个体的成分，个体还可含有适度值等成分。个体、染色体、位串或字符串有时在遗传算法中可不加区分地使用。
(4)种群规模(population scale)：又称种群大小，指种群中所含个体的数目。
(5)基因(gene)：位串中的每个位或元素统称为基因。基因反映个体的特征。同一位上的基因不同，个体的特征可能也不相同。基因对应于遗传学中的遗传物质单位。在 DNA 序列表示中，遗传物质单位也是用特定编码表示的。遗传算法中扩展了编码的概念，对于可行解，可用 0、1 二值、0~9 十个数字, 以及其他形式的编码表示。例如，在 0、1 二值编码下，有一个串 S=1011，则其中的 1，0，1，1 这 4 个元素分别称为基因。基因和位在遗传算法中也可不加区分地使用。
(6)适应度(fitness)：个体对环境的适应程度称为适应度(fitness)。为了体现染色体的适应能力，通常引入一个对每个染色体都能进行度量的函数,称为适应度函数。
(7)选择(selection)：在整个种群或种群的一部分中选择某个个体的操作。
(8)交叉(crossover)：两个个体对应的一个或多个基因段的交换操作。
(9)变异(mutation)：个体位串上某个基因的取值发生变化。如在 0、1 串表示下，某位的值从 0 变为 1，或由 1 变为 0。
遗传算法的基本流程如下：

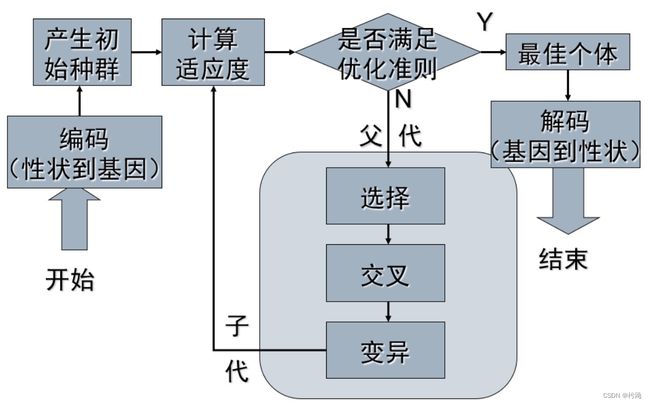
本案例意在说明如何使用遗传算法求解无约束单目标优化问题，即求一元函数：
$$\mathbf{f}(\mathbf{x})=\mathbf{x}\cdot \sin (10\mathbf{\pi }\cdot \mathbf{x})+2$$
在区间 [-1, 2] 上的最大值。该函数图像如下：
由图像可知该函数在在区间 [-1, 2] 上有很多极大值和极小值，对于求其最大值或最小值的问题，很多单点优化的方法(梯度下降等)就不适合，这种情况下可以考虑使用遗传算法。

完整代码及注释讲解

import numpy as np
import matplotlib.pyplot as plt


def fun(x):
    return x * np.sin(10*np.pi*x) + 2


Xs = np.linspace(-1, 2, 100)

np.random.seed(0)  # 令随机数种子=0，确保每次取得相同的随机数

# 初始化原始种群
population = np.random.uniform(-1, 2, 10)  # 在[-1,2)上以均匀分布生成10个浮点数，做为初始种群

for pop, fit in zip(population, fun(population)):
    print("x=%5.2f, fit=%.2f" % (pop, fit))

plt.plot(Xs, fun(Xs))
plt.plot(population, fun(population), '*')
plt.show()


def encode(population, _min=-1, _max=2, scale=2**18, binary_len=18):  # population必须为float类型，否则精度不能保证
    # 标准化，使所有数据位于0和1之间,乘以scale使得数据间距拉大以便用二进制表示
    normalized_data = (population-_min) / (_max-_min) * scale
    # 转成二进制编码
    binary_data = np.array([np.binary_repr(x, width=binary_len)
                           for x in normalized_data.astype(int)])
    return binary_data


chroms = encode(population)  # 染色体英文(chromosome)


for pop, chrom, fit in zip(population, chroms, fun(population)):
    print("x=%.2f, chrom=%s, fit=%.2f" % (pop, chrom, fit))


def decode(popular_gene, _min=-1, _max=2, scale=2**18):  # 先把x从2进制转换为10进制，表示这是第几份
    # 乘以每份长度（长度/份数）,加上起点,最终将一个2进制数，转换为x轴坐标
    return np.array([(int(x, base=2)/scale*3)+_min for x in popular_gene])



fitness = fun(decode(chroms))

for pop, chrom, dechrom, fit in zip(population, chroms, decode(chroms), fitness):
    print("x=%5.2f, chrom=%s, dechrom=%.2f, fit=%.2f" %
          (pop, chrom, dechrom, fit))

fitness = fitness - fitness.min() + 0.000001  # 保证所有的都为正
print(fitness)

# 选择和交叉
def Select_Crossover(chroms, fitness, prob=0.6):  
    probs = fitness/np.sum(fitness)  # 各个个体被选择的概率
    probs_cum = np.cumsum(probs)  # 概率累加分布

    each_rand = np.random.uniform(size=len(fitness))  # 得到10个随机数，0到1之间

    # 轮盘赌，根据随机概率选择出新的基因编码
    # 对于each_rand中的每个随机数，找到被轮盘赌中的那个染色体
    newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
                    for rand in each_rand])

    # 繁殖，随机配对（概率为0.6)
    # 6这个数字怎么来的，根据遗传算法，假设有10个数，交叉概率为0.6，0和1一组，2和3一组。。。8和9一组，每组扔一个0到1之间的数字
    # 这个数字小于0.6就交叉，则平均下来应有三组进行交叉，即6个染色体要进行交叉
    pairs = np.random.permutation(
        int(len(newX)*prob//2*2)).reshape(-1, 2)  # 产生6个随机数，乱排一下，分成二列
    center = len(newX[0])//2  # 交叉方法采用最简单的，中心交叉法
    for i, j in pairs:
        # 在中间位置交叉
        x, y = newX[i], newX[j]
        newX[i] = x[:center] + y[center:]  # newX的元素都是字符串，可以直接用+号拼接
        newX[j] = y[:center] + x[center:]
    return newX


chroms = Select_Crossover(chroms, fitness)

dechroms = decode(chroms)
fitness = fun(dechroms)

for gene, dec, fit in zip(chroms, dechroms, fitness):
    print("chrom=%s, dec=%5.2f, fit=%.2f" % (gene, dec, fit))

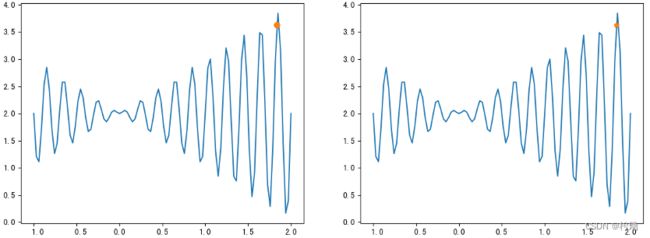
# 对比一下选择和交叉之后的结果
fig, (axs1, axs2) = plt.subplots(1, 2, figsize=(14, 5))
axs1.plot(Xs, fun(Xs))
axs1.plot(population, fun(population), 'o')
axs2.plot(Xs, fun(Xs))
axs2.plot(dechroms, fitness, '*')
plt.show()

# 变异
# 输入一个原始种群1，输出一个变异种群2  函数参数中的冒号是参数的类型建议符，告诉程序员希望传入的实参的类型。函数后面跟着的箭头是函数返回值的类型建议符，用来说明该函数返回的值是什么类型。
def Mutate(chroms: np.array):
    prob = 0.1  # 变异的概率
    clen = len(chroms[0])  # chroms[0]="111101101 000010110"    字符串的长度=18
    m = {'0': '1', '1': '0'}  # m是一个字典，包含两对：第一对0是key而1是value；第二对1是key而0是value
    newchroms = []  # 存放变异后的新种群
    each_prob = np.random.uniform(size=len(chroms))  # 随机10个数

    for i, chrom in enumerate(chroms):  # enumerate的作用是整一个i出来
        if each_prob[i] < prob:  # 如果要进行变异(i的用处在这里)
            pos = np.random.randint(clen)  # 从18个位置随机中找一个位置，假设是7
            # 0~6保持不变，8~17保持不变，仅将7号翻转，即0改为1，1改为0。注意chrom中字符不是1就是0
            chrom = chrom[:pos] + m[chrom[pos]] + chrom[pos+1:]
        newchroms.append(chrom)  # 无论if是否成立，都在newchroms中增加chroms的这个元素
    return np.array(newchroms)  # 返回变异后的种群


newchroms = Mutate(chroms)


def DrawTwoChroms(chroms1, chroms2, fitfun):  # 画2幅图，左边是旧种群，右边是新种群，观察平行的两幅图可以看出有没有差异
    Xs = np.linspace(-1, 2, 100)
    fig, (axs1, axs2) = plt.subplots(1, 2, figsize=(14, 5))
    dechroms = decode(chroms1)
    fitness = fitfun(dechroms)
    axs1.plot(Xs, fitfun(Xs))
    axs1.plot(dechroms, fitness, 'o')

    dechroms = decode(chroms2)
    fitness = fitfun(dechroms)
    axs2.plot(Xs, fitfun(Xs))
    axs2.plot(dechroms, fitness, '*')
    plt.show()


# 对比一下变异前后的结果
DrawTwoChroms(chroms, newchroms, fun)

# 上述代码只是执行了一轮，这里反复迭代
np.random.seed(0)  # 
population = np.random.uniform(-1, 2, 100)  # 这次多找一些点，在[-1,2)上以均匀分布生成 100 个浮点数，做为初始种群
chroms = encode(population)# 染色体英文(chromosome)

for i in range(1000):
    fitness = fun(decode(chroms))
    fitness = fitness - fitness.min() + 0.000001  # 保证所有的都为正
    newchroms = Mutate(Select_Crossover(chroms, fitness))
    if i % 300 == 1:
        DrawTwoChroms(chroms, newchroms, fun)
    chroms = newchroms

DrawTwoChroms(chroms, newchroms, fun)

实验内容

1）代码第 64 行的语义是什么？两个[0]各自代表什么？最后 newX 有几个元素？

newX = np.array([chroms[np.where(probs_cum > rand)[0][0]] for rand in each_rand])

语义：进行轮盘赌，对于 each_rand 中的每个随机数（即随机概率），找到被轮盘赌中的那个染色体，选择出新的基因编码。每一轮for循环都将概率累加分布与随机数相比较，where[0][0]的用途是返回第一个概率累加分布符合大于该随机数这一条件的染色体的坐标，chroms[where[0][0]]是返回该坐标下具体的值，加入到newX中。
where函数返回满足条件的元素的坐标（索引），以元组的形式给出，原数组有多少维，输出的元组就包含几个数组，分别对应符合条件的元素的各维坐标。第一个[0]把返回的1维元组转换（取出来）成numpy，即返回元组中的第一个数组的值。第二个[0]将返回的第一个数组的第一个（首个）元素提取出来（即只要满足条件的众多染色体的第一个染色体）。
最后的newX的个数与原种群的个数相等。

2）代码第 70 行的语义是什么？为什么要除以 2 再乘以 2？reshape 中的-1 表示什么？

pairs = np.random.permutation(int(len(newX)*prob//2*2)).reshape(-1, 2)
# 产生 6 个随机数乱排一下分成二列

语义：以prob的概率生成随机数（数的个数是prob✖️种群数），并将它们随机排序，返回一个两列的二维数组。这个数组即为即将进行交叉操作的染色体的下标。
除以2再乘以2是因为种群数✖️prob不一定是偶数，先除以2再乘以2保证了被选中的随机数的个数一定是偶数，便于之后将随机数分成两列。
reshape中的 -1 是指在指定新数组是2列的情况下，代码自动根据剩余的维度计算出其合适的行数。

3）请结合 Mutate 函数的内容，详述变异是如何实现的。

首先将变异的概率设置为0.1，将变异的规则设置为如果该位是0则变成1，如果该位是1则变成0。设置一个新数组newchroms来存放变异后的新种群，随机生成个数与种群数相等的数来作为该染色体是否进行变异的标准，如果该随机数小于变异概率，则该随机数所对应的染色体将进行变异。
变异的过程是：在该染色体的18 个位置中随机找一个位置，该位置上的数字根据变异规则进行变异，改染色体其余位置上的数字不变，这样就完成了一个染色体的变异，将变异后的染色体增加到newchroms中。如果该染色体没有参与变异，就将该染色体原封不动地加入到newchroms中。

4）将代码第 145 行（本文中上面代码的第114行，老师给的代码的第115行）修改为 newchroms = Select_Crossover(chroms, fitness)，即不再执行变异，执行结果有什么不同，为什么会出现这种变化？

原结果：
fitness:
[3.82459416 3.82336222 3.84093277 3.84903836 3.83100028 3.57486113
3.83533168 3.82358835 3.82256332 3.79725184 3.82336222 3.83090421
3.80536872 0.21547799 3.81535968 3.83090421 3.54063999 3.84903836
3.82279276 3.83022504 3.83100028 3.81637916 3.81523119 3.80316259
3.41496509 3.84093277 3.81961525 3.83166612 3.81523119 3.81497352
3.81637916 3.81535968 3.85016146 3.84093277 3.85010429 3.81432527
3.81497352 3.82676046 3.81432527 3.83012706 3.81961525 3.81535968
3.80316259 3.81535968 3.82676046 3.82676046 3.80551394 3.82244824
3.84906254 3.54063999 3.82267816 3.82244824 3.80551394 3.82983171
3.82336222 3.83100028 3.81535968 3.81837332 3.82676046 3.81961525
3.81406434 3.00265704 3.81406434 3.80551394 3.83012706 3.80536872
3.82336222 3.70988636 3.83100028 3.79686713 3.79189073 3.85026849
3.83501307 3.83012706 3.83002885 3.82244824 3.85016867 3.83022504
3.81221172 3.11204063 3.82336222 3.79527283 3.83012706 3.81406434
3.81432527 3.80536872 3.83769464 3.82336222 3.81961525 3.84093277
3.84066344 3.84093277 3.82676046 3.83501307 3.80551394 3.83100028
3.82256332 3.82963362 3.80551394 3.83012706]

执行变异操作最后结果展示图：

不执行变异后结果：
fitness:
[3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208 3.63404208 3.63404208
3.63404208 3.63404208 3.63404208 3.63404208]

不执行变异操作最后结果展示图：

不执行变异后种群都聚集在同一个地方，且前后两次种群的差异不大，最后得到的结果也没有执行变异时好。
原因：
选择和交叉是在原种群的基础上选择更好的去进行发展，其能否到达最优点与初始种群关系很大，且整个种群没有异变，使得最后所有的染色体都会向初始种群中最好的那个染色体的值趋近，即最后种群都聚集在同一个地方。如果初始种群中没有整体的最优解，那么很有可能最后找不到最优解。
引入了变异后使得整个种群中有异变的个体，使新种群不再只从原种群中的值中进行选择，增加了染色体的多样性，最后的结果也不再只依赖于初始种群，所以最后的结果不会都聚集在同一个地方，且前后两次种群的差异也会变大，也有更大的概率去获得最优解。

5）轮盘让个体按概率被选择，对于适应度最高的个体而言，虽然被选择的概率高，但仍有可能被淘汰，从而在进化过程中失去当前最优秀的个体。一种改进方案是，让适应度最高的那个个体不参与选择，而是直接进入下一轮（直接晋级），这种方案被称为精英选择(elitist selection)。请修改Select 部分的代码，实现这一思路。

将本文上面的原代码第56-78行代码修改为：

# 选择和交叉
def Select_Crossover(chroms, fitness, prob=0.6):
.   #修改处
   probs = fitness/np.sum(fitness) # 各个个体被选择的概率
   
   prob_max_index = (np.where(probs == np.max(probs))[0][0])  # 获取适应度最大的元素的位置
   prob_max_chrom = chroms[prob_max_index] # 记录下适应度最大的染色体
   chroms = np.delete(chroms, prob_max_index) # 从种群中删除适应度最大的染色体，避免选择时被选择
   probs = np.delete(probs, prob_max_index) # 删除适应度最大的概率，避免影响累加结果
   
   probs_cum = np.cumsum(probs)  # 概率累加分布
   rand_max = probs_cum[len(probs_cum)-1] # 得到probs_cum的最大值，避免生成随机数时，随机数的值超过该最大值

   each_rand = np.random.uniform(low=0,high=rand_max,size=len(fitness)-1)  # 得到 9 个随机数 0 到 rand_max 之间

   newX = np.array([chroms[np.where(probs_cum > rand)[0][0]] for rand in each_rand])
   newX = np.append(newX, prob_max_chrom)  # 最后把适应度最大的染色体添加到新种群中

   # 繁殖，随机配对（概率为 0.6)

   # 以 0.6 的概率交叉，则平均下来应有三组进行交叉，即 6 个染色体要进行交叉
   pairs = np.random.permutation(int(len(newX)*prob//2*2)).reshape(-1, 2) # 产生 6 个随机数，乱排一下，分成二列（np.random.permutation 随机排序）
   center = len(newX[0])//2 # 交叉方法采用最简单的，中心交叉法
   for i, j in pairs:
       # 在中间位置交叉
       x, y = newX[i], newX[j]
       newX[i] = x[:center] + y[center:] # newX 的元素都是字符串，直接用+号拼接
       newX[j] = y[:center] + x[center:]
   return newX

代码运行结果：
fitness：
[3.81002226 3.711904 3.711904 3.79055269 3.84602091 3.84707934
3.84602091 3.84570525 3.84408613 2.94970777 3.80068414 3.84570525
3.84767447 3.84570525 3.8448756 3.82590534 3.79055269 2.10223215
3.83775991 3.84570525 3.84570525 3.84556387 3.45796475 3.84602091
3.84570525 3.78783178 3.84561124 3.84565836 1.67134951 3.78469935
3.74929994 3.78505113 3.79055269 2.93604353 3.79004708 3.84565836
2.94970777 3.79055269 3.84561124 3.84492632 3.84565836 3.79055269
3.84492632 3.84397681 3.75940866 1.51502464 3.79055269 3.76919325
3.83775991 3.79038439 3.79055269 2.93604353 3.79055269 3.79038439
3.79055269 3.84556387 3.76899899 3.84602091 3.8497307 2.78719053
3.83775991 3.79038439 3.79055269 3.84565836 3.79055269 3.8497307
3.84570525 3.79055269 1.70228516 3.79004708 3.83775991 3.78783178
3.84983393 3.83775991 3.83775991 3.79038439 3.79038439 3.76899899
3.84565836 3.77547675 3.84570525 1.77057756 3.81016051 3.64320772
3.81016051 3.84570525 3.78783178 3.78469935 3.79055269 3.83775991
3.84565836 3.84983393 3.84408613 3.84565836 3.84492632 3.8497307
3.79038439 3.84492632 3.81016051 3.85008836]

进行精英选择操作最后结果展示图：

6）【选做】请借鉴示例代码，实现教材P57的例2.6.1，即用遗传算法求解下列二元函数的最大值。注意：不允许分开求解${\mathbf{x}}_1\cdot \sin (4\mathbf{\pi }\cdot {\mathbf{x}}_1)$和${\mathbf{x}}_2\cdot \sin (20\mathbf{\pi }\cdot {\mathbf{x}}_2)$的最大值再合并。
$$\begin{gathered} \max \mathbf{f}({\mathbf{x}}_1,{\mathbf{x}}_2)=21.5+{\mathbf{x}}_1\cdot \sin (4\mathbf{\pi }\cdot {\mathbf{x}}_1)+{\mathbf{x}}_2\cdot \sin (20\mathbf{\pi }\cdot {\mathbf{x}}_2) \\ \mathbf{s}.\mathbf{t}.\begin{array}{c}-2.9\le x_1\le 12.0\\ 4.2\le x_2\le 5.7\end{array} \end{gathered}$$

代码修改后如下：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def fun(x1, x2):
   return 21.5 + x1*np.sin(4*np.pi*x1) + x2*np.sin(20*np.pi*x2)

X1 = np.linspace(-2.9, 12.0, 100)
X2 = np.linspace(4.2, 5.7, 100)

np.random.seed(0) # 令随机数种子=0，确保每次取得相同的随机数

# 初始化原始种群 
population1 = np.random.uniform(-2.9, 12.0, 10) 
# 在[-2.9,12)上以均匀分布生成 10 个浮点数，做为初始种群 
population2 = np.random.uniform(4.2,5.7, 10) 
# 在[4.2,5.7)上以均匀分布生成 10 个浮点数，做为初始种群 
for pop1, pop2, fit in zip(population1, population2, fun(population1, population2)):
    print("x1=%5.2f, x2=%5.2f, fit=%.2f" % (pop1, pop2, fit))

# 新建一个画布 
figure = plt.figure()
# 新建一个3d绘图对象 
ax = Axes3D(figure)

# 生成x1, x2 的坐标集 
x1 = np.linspace(-2.9, 12.0, 20) 
x2 = np.linspace(4.2, 5.7, 17)

# 生成网格矩阵 
X1, X2 = np.meshgrid(x1, x2)

# 定义x1,x2 轴名称 
plt.xlabel("x1") 
plt.ylabel("x2")

Z = 21.5+X1*np.sin(4*X1*np.pi)+X2*np.sin(20*X2*np.pi)
# 设置间隔和颜色 
ax.plot_surface(X1, X2, Z, rstride=1, cstride=1, cmap="PuBuGn",alpha=0.5)
#ax.plot_wireframe(X,Y,Z) 
ax.set_zlim(0, 40) 
ax.scatter(population1,population2,fun(population1,population2),marker='.', color='black')
# 展示 
plt.show()

# 编码 
def encode(population, _min, _max, scale=2**18, binary_len=18): # population 必须为float 类型，否则精度不能保证
    # 标准化，使所有数据位于 0 和 1 之间,乘以 scale 使得数据间距拉大以便用二进制表示
    normalized_data = (population-_min) / (_max-_min) * scale
    # 转成二进制编码
    binary_data = np.array([np.binary_repr(x, width=binary_len) for x in normalized_data.astype(int)])
    return binary_data

chroms1 = encode(population1, -2.9, 12) # 染色体英文(chromosome) 
chroms2 = encode(population2, 4.2, 5.7) # 染色体英文(chromosome)

for pop1, pop2, chrom1, chrom2, fit in zip(population1, population2,chroms1, chroms2, fun(population1, population2)):
    print("x1=%.2f, x2=%.2f, chrom1=%s, chrom2=%s, fit=%.2f" % (pop1, pop2, chrom1, chrom2, fit))

# 解码 
def decode(popular_gene, _min, _max, scale=2**18): # 先把 x 从 2 进制转换为 10 进制，表示这是第几份
    # 乘以每份长度（长度/份数）,加上起点,最终将一个 2 进制数，转换为 x 轴坐标
    return np.array([(int(x, base=2)/scale*(_max-_min))+_min for x in popular_gene])

fitness = fun(decode(chroms1, -2.9, 12), decode(chroms2, 4.2, 5.7))

for pop1, pop2, chrom1, chrom2, dechrom1, dechrom2, fit in zip(population1, population2, chroms1, chroms2, decode(chroms1, -2.9,12), decode(chroms2, 4.2, 5.7), fitness):
    print("x1=%5.2f, x2=%5.2f, chrom1=%s, chrom2=%s, dechrom1=%.2f, dechrom2=%.2f, fit=%.2f" %(pop1, pop2, chrom1, chrom2, dechrom1,dechrom2, fit))

fitness = fitness - fitness.min() + 0.000001 # 保证所有的都为正 
print(fitness)

# 选择和交叉 
def Select_Crossover(chroms1, chroms2, fitness, prob=0.6):
    probs = fitness/np.sum(fitness) # 各个个体被选择的概率
    probs_cum = np.cumsum(probs)  # 概率累加分布
    
    each_rand = np.random.uniform(size=len(fitness)) # 得到 10 个随机数 0 到 1 之间
    newX1 = np.array([chroms1[np.where(probs_cum > rand)[0][0]] for rand in each_rand])
    newX2 = np.array([chroms2[np.where(probs_cum > rand)[0][0]] for rand in each_rand])
    
    # 繁殖，随机配对（概率为 0.6)

    # 以 0.6 的概率交叉，则平均下来应有三组进行交叉，即 6 个染色体要进行交叉
    pairs = np.random.permutation(int(len(newX1)*prob//2*2)).reshape(-1, 2) # 产生 6 个随机数，乱排一下，分成二列（np.random.permutation 随机排序）
    center = len(newX1[0])//2 # 交叉方法采用最简单的，中心交叉法
    for i, j in pairs:
        # 在中间位置交叉
        x11, x12 = newX1[i], newX2[i]
        x21, x22 = newX1[j], newX2[j]
        newX1[i] = x11[:center] + x21[center:] # newX 的元素都是字符串，直接用+号拼接
        newX1[j] = x21[:center] + x11[center:]
        newX2[i] = x12[:center] + x22[center:]  # newX 的元素都是字符串，直接用+号拼接
        newX2[j] = x22[:center] + x12[center:]
    return newX1, newX2


chroms = Select_Crossover(chroms1, chroms2, fitness)

dechrom1 = decode(chroms[0], -2.9, 12) 
dechrom2 = decode(chroms[1],4.2, 5.7) 
fitness = fun(dechrom1, dechrom2)

for gene1, gene2, dec1, dec2, fit in zip(chroms[0], chroms[1],dechrom1, dechrom2, fitness):
    print("chrom1=%s, chrom2=%s, dec1=%5.2f, dec2=%5.2f, fit=%.2f" % (gene1, gene2, dec1, dec2, fit))

# 新建一个画布 
figure = plt.figure()
# 新建一个3d绘图对象 
ax1 = figure.add_subplot(1,2,1,projection='3d') 
ax2 = figure.add_subplot(1,2,2,projection='3d')
# 生成x1, x2 的坐标集 
x1 = np.linspace(-2.9, 12.0, 20) 
x2 = np.linspace(4.2, 5.7, 17)
# 生成网格矩阵 
X1, X2 = np.meshgrid(x1, x2)
# 定义x1,x2 轴名称 
plt.xlabel("x1") 
plt.ylabel("x2") 
Z = 21.5+X1*np.sin(4*X1*np.pi)+X2*np.sin(20*X2*np.pi)
# 设置间隔和颜色 
ax1.plot_surface(X1, X2, Z, rstride=1, cstride=1, cmap="PuBuGn",alpha=0.5)
ax1.set_zlim(0, 40) 
ax1.scatter(population1,population2, fun(population1, population2), marker='.', color='black')
ax2.plot_surface(X1, X2, Z, rstride=1, cstride=1,cmap="PuBuGn",alpha=0.5)
ax2.set_zlim(0, 40) 
ax2.scatter(dechrom1,dechrom2, fitness, marker='*', color='black')
# 展示 
plt.show()

# 变异
# 输入一个原始种群 1，输出一个变异种群 2 ，函数参数中的冒号是参数的类型建议符 
def Mutate(chroms: np.array):
    prob = 0.1 # 变异的概率
    clen = len(chroms[0][0]) # chroms[0]="111101101 000010110" 字符串的长度=18
    m = {'0': '1', '1': '0'} # m 是一个字典，包含两对：第一对 0 是 key 而 1 是 value；第二对 1 是 key 而 0 是 value
    newchroms1 = [] # 存放变异后的新种群
    newchroms2 = []
    each_prob = np.random.uniform(size=len(chroms[0])) # 随机 10 个数
    for i, chrom1 in enumerate(chroms[0]): # enumerate 的作用是整一个 i 出来（同时列出数据和数据下标）
        if each_prob[i] < prob: # 如果要进行变异(i 的用处在这里)
            pos = np.random.randint(clen) # 从 18 个位置随机找一个位置，假设是 7
            # 0～6保持不变，8~17 保持不变，仅将 7 号翻转，即 0 改为 1，1 改为 0。注意 chrom 中字符不是 1 就是 0
            chrom1 = chrom1[:pos] + m[chrom1[pos]] + chrom1[pos+1:]
        newchroms1.append(chrom1) # 无论 if 是否成立，都在 newchroms 中增加 chroms 的这个元素
    for i, chrom2 in enumerate(chroms[1]): # enumerate 的作用是整一个 i 出来（同时列出数据和数据下标）
        if each_prob[i] < prob: # 如果要进行变异(i 的用处在这里)
            pos = np.random.randint(clen) # 从 18 个位置随机找一个位置，假设是 7
            # 0～6 保持不变，8~17 保持不变，仅将 7 号翻转，即 0 改为 1，1 改为 0。注意 chrom 中字符不是 1 就是 0
            chrom2 = chrom2[:pos] + m[chrom2[pos]] + chrom2[pos+1:]
        newchroms2.append(chrom2) # 无论 if 是否成立，都在 newchroms 中增加 chroms 的这个元素
    return newchroms1, newchroms2 # 返回变异后的种群

newchroms = Mutate(chroms)

def DrawTwoChroms(chroms1, chroms2, fitfun): # 画 2 幅图，左边是旧种群，右边是新种群
    # 新建一个画布
    figure = plt.figure()
    # 新建一个3d绘图对象
    ax1 = figure.add_subplot(1, 2, 1, projection='3d')
    ax2 = figure.add_subplot(1, 2, 2, projection='3d')

    # 生成x, y 的坐标集 (-2,2) 区间，间隔为 0.1
    x = np.linspace(-2.9, 12.0, 20)
    y = np.linspace(4.2, 5.7, 18)

    # 生成网格矩阵
    X, Y = np.meshgrid(x, y)

    # 定义x,y 轴名称
    plt.xlabel("x")
    plt.ylabel("y")
    # 设置间隔和颜色
    ax1.plot_surface(X1, X2, Z, rstride=1, cstride=1, cmap="PuBuGn", alpha=0.5)
    ax1.set_zlim(0, 40)
    ax1.scatter(decode(chroms1[0], -2.9, 12), decode(chroms1[1], 4.2, 5.7), fitfun(decode(chroms1[0], -2.9, 12), decode(chroms1[1], 4.2, 5.7)), marker='.', color='black')
    ax2.plot_surface(X1, X2, Z, rstride=1, cstride=1, cmap="PuBuGn", alpha=0.5)
    ax2.set_zlim(0, 40)
    ax2.scatter(decode(chroms2[0], -2.9, 12),  decode(chroms2[1], 4.2, 5.7), fitfun(decode(chroms2[0], -2.9, 12), decode(chroms2[1], 4.2, 5.7)), marker='*', color='black')
    plt.show()

# 对比一下变异前后的结果 
DrawTwoChroms(chroms, newchroms, fun)

# 上述代码只是执行了一轮，这里反复迭代 
np.random.seed(0) 
population1 = np.random.uniform(-2.9, 12.0, 100) # 在[-2.9,12)上以均匀分布生成 100 个浮点数，做为初始种群 
population2 = np.random.uniform(4.2, 5.7, 100) # 在[4.2,5.7)上以均匀分布生成 100 个浮点数，做为初始种群 
chroms1 = encode(population1, -2.9,12) # 染色体英文(chromosome) 
chroms2 = encode(population2, 4.2, 5.7) # 染色体英文(chromosome)

for i in range(1000):
    fitness = fun(decode(chroms1, -2.9, 12), decode(chroms2, 4.2, 5.7))
    fitness = fitness - fitness.min() + 0.000001 # 保证所有的都为正
    newchroms = Mutate(Select_Crossover(chroms1, chroms2, fitness))
    chroms =  np.c_[chroms1, chroms2]
    if i % 300 == 1:
        DrawTwoChroms(chroms, newchroms, fun)
    chroms1 = newchroms[0]
    chroms2 = newchroms[1]

chroms =  np.c_[chroms1, chroms2] 
DrawTwoChroms(chroms, newchroms,fun) 
print(fun(decode(newchroms[0], -2.9, 12), decode(newchroms[1],4.2, 5.7)))

运行结果：
fitness：
[20.97512885 37.93558901 38.01362399 37.78089186 37.62876192 37.76508764 38.01187147 35.26228182 9.15817839 36.94172309 37.9834056 38.01604785 38.01362399 35.58509904 38.01273391 38.02589359 33.31239497 37.62876192 38.01273391 37.92891492 37.98471789 37.48412205 37.92715132 38.0143306 37.68316903 35.97186115 38.0143306 37.62876192 38.01604785 37.4779909 36.03163445 38.01604785 35.80298233 38.02589359 37.9320919 38.01604785 38.0143306 36.94172309 36.94172309 38.01187147 38.01362399 26.66995785 37.73244539 37.84509809 38.01604785 33.67732575 37.95100661 37.9834056 37.9834056 37.78089186 37.84509809 18.85887675 37.73244539 36.07079067 38.01273391 23.64723757 29.67665868 36.94172309 37.98486661 37.98471789 37.72815579 37.76269133 37.9834056 38.01604785 37.98486661 37.4779909 37.45355893 38.01604785 37.95100661 37.95100661 37.48412205 8.33027485 37.76508764 37.92715132 36.35993399 37.62876192 37.62876192 37.62876192 37.93709313 37.9320919 37.95100661 37.9320919 37.72815579 37.95100661 37.89876282 25.32962488 37.9834056 33.24604268 37.4779909 37.73322734 37.48412205 38.02589359 37.94668373 37.62876192 37.48412205 38.01604785 25.04039919 38.02589359 38.02589359 29.67279852]

变化过程：
100个染色体第1次迭代结果示意图：
100个染色体第301次迭代结果示意图：
100个染色体第601次迭代结果示意图：
100个染色体第901次迭代结果示意图：
100个染色体第1000次迭代结果示意图：

实验结果与分析

在第4）小题中，当代码不再执行变异时，训练后的样本全都聚集在一起，并且前后两次训练结果差别不大，最后的结果也远不如有变异时的结果。说明变异可以让整个种群引入新的个体，增加了染色体的多样性，增大了找到最优解的概率并且避免陷入局部最优，变异是遗传算法中不可替代的一环，其使找到最优解的过程不再只依赖于初始种群。
第5）小题中，精英选择策略最后的整体结果要好于不使用精英选择策略时，使用精英选择策略时，最后的结果不再有个体仍处于最低点的位置。

实验小结

本实验应重点理解各阶段的具体过程，虽然代码很长，但是一行一行debug下来就会对这段代码有很清晰的认知，难度不大但是需要耐心。5）、6）两小题是比较有意思的题目，值得反复揣摩。