再识二叉树

1. 二叉树的存储

        二叉树的存储结构分为：顺序存储和类似于链表的链式存储。 其中二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方式（这里本主主要讲的是链式存储），具体代码如下：

        二叉表示：

// 孩子表示法
class Node {
	int val; // 数据域
	Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
	Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}

        三叉表示： 

// 孩子双亲表示法
class Node {
	int val; // 数据域
	Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
	Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
	Node parent; // 当前节点的根节点
}

         注意：本主本篇创建的二叉树都是基于二叉表示的；

2、二叉树的遍历

2.1 通过代码了解二叉树

        在学习二叉树的基本操作前，首先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习；

        通过以下代码我们可以构造一个简单的二叉树。

import com.sun.org.apache.regexp.internal.RE;

import java.util.concurrent.Callable;

public class BinaryTree {
    static class TreeNode{
        public char value;
        public TreeNode left;
        public TreeNode right;
        public TreeNode(char value){
            this.value = value;
        }
    }
    //创建一棵二叉树 创建成功后 返回根节点A
    public TreeNode createTree(){
        TreeNode A = new TreeNode('A');
        TreeNode B = new TreeNode('B');
        TreeNode C = new TreeNode('C');
        TreeNode D = new TreeNode('D');
        TreeNode E = new TreeNode('E');
        TreeNode F = new TreeNode('F');
        TreeNode G = new TreeNode('G');
        TreeNode H = new TreeNode('H');
        A.left = B;
        A.right = C;
        B.left = D;
        B.right = E;
        C.left = F;
        C.right = G;
        E.right = H;
        return  A;
    }
}

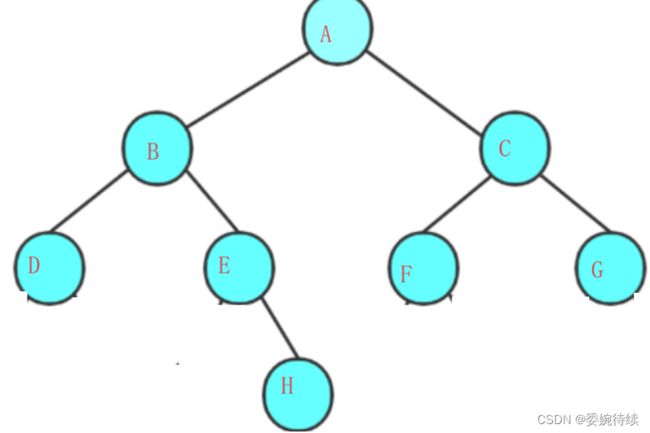
        下图就是我们代码构造的二叉树图； 

                       

        注意：上述代码并不是创建二叉树的方式,而是我们用代码讲二叉树详细的描述出来；我们通过前一张的内容学习知道二叉树是递归式的（整个树从下到上，从左到右，每一个左节点和右节点与根节点三方面构成一个小树，由此可知每一个左子树和右子树与根节点构成二叉树），因此后序二叉树的基本操作中基本都是按照该递归概念实现的。

2.2 二叉树的遍历详解

        所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结 点均做一次且仅做一次访问

（依次对树中每个结点有且仅做一次访问）到一个节点并不一定要遍历该节点；

        在遍历二叉树时，如果没有进行某种约定，每个人都按照自己的方式遍历，得出的结果就比较混乱，如果按照某种规则进行约定，则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点，L代表根节点的左子树，R代表根节点的右子树，则根据遍历根节点的先后次序有以下遍历方式：

NLR：前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点—>根的左子树—>根的右子树。

LNR：中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树。

LRN：后序遍历(Postorder Traversal)——根的左子树—>根的右子树—>根节点

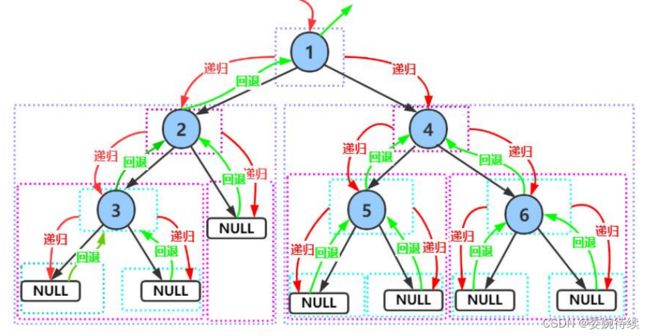
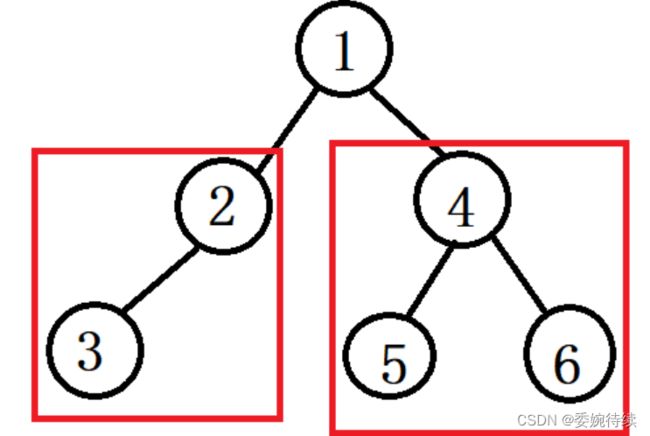
        如下图的二叉树通过详细的递归的思路进行遍历，按照不同的遍历方式我们可以得到不同的访问结果，其二叉树如下图所示：

        以下是该二叉树的三种遍历的结果： 

前序遍历结果：1 2 3 4 5 6

中序遍历结果：3 2 1 5 4 6

后序遍历结果：3 1 5 6 4 1

        我们接下来详细的分析一下三种遍历的过程；

2.2.1 前序遍历

1.从1节点开始，遍历1结点--->

2. 递归到1结点的左子树，遍历2节点--->

3. 递归到2结点的左子树，遍历3节点--->

4. 递归到3结点的左子树，该节点为null，回退到3节点--->

5. 递归到3结点的右子树，该节点为null，回退到3节点，3节点已经被遍历，回退到2节点--->

6. 递归到2结点的右子树，该节点为null，回退到2节点，2节点已经被遍历，回退到1节点，1节点已经被遍历--->

7. 递归到1结点的右子树，遍历4节点--->

8. 递归到4结点的左子树，遍历5节点--->

9. 递归到5结点的左子树，该节点为null，回退到5节点，5节点已经被遍历，回退到4节点--->

10. 递归到4结点的右子树，遍历6节点--->

11. 递归到6结点的左子树，该节点为null，回退到6节点--->

12. 递归到6结点的右子树，该节点为null，此刻6节点是整个树的最右节点，此时遍历结束

2.2.2 中序遍历

1.从1节点开始--->

2. 递归到1结点的左子树--->

3. 递归到2结点的左子树--->

4. 递归到3结点的左子树，该节点为null，回退到3节点，此时遍历3节点--->

5. 递归到3结点的右子树，该节点为null，回退到3节点，3节点已经被遍历，回退到2节点，此时遍历2节点--->

6. 递归到2结点的右子树，该节点为null，回退到2节点，2节点已经被遍历，回退到1节点，此时遍历1节点--->

7. 递归到1结点的右子树，到达4节点--->

8. 递归到4结点的左子树，到达5节点--->

9. 递归到5结点的左子树，该节点为null，回退到5节点，此时遍历5节点-->

10.递归到5节点的右子树，该节点为空，回退到5节点，其次回退到4节点,此时遍历4节点--->

12. 递归到4结点的右子树，到达6节点--->

12. 递归到6结点的左子树，该节点为null，回退到6节点，此时遍历6节点--->

13. 递归到6结点的右子树，该节点为null，此刻6节点是整个树的最右节点，此时遍历结束

2.2.3 后序遍历

1.从1节点开始--->

2. 递归到1结点的左子树--->

3. 递归到2结点的左子树--->

4. 递归到3结点的左子树，该节点为null，回退到3节点--->

5. 递归到3结点的右子树，该节点为null，回退到3节点，此时遍历3节点，回退到2节点--->

6. 递归到2结点的右子树，该节点为null，回退到2节点，此时遍历2节点，回退到1节点--->

7. 递归到1结点的右子树，到达4节点--->

8. 递归到4结点的左子树，到达5节点--->

9. 递归到5结点的左子树，该节点为null，回退到5节点-->

10.递归到5节点的右子树，该节点为空，回退到5节点，此时遍历5节点；其次回退到4节点,--->

12. 递归到4结点的右子树，到达6节点--->

12. 递归到6结点的左子树，该节点为null，--->

13. 递归到6结点的右子树，该节点为null，回退到6节点，此时遍历6节点；

14、其次回退到4节点,此时遍历4节点-->

15、其次回退到1节点,此时遍历1节点-->此刻1节点是整个树的根点，此时遍历结束

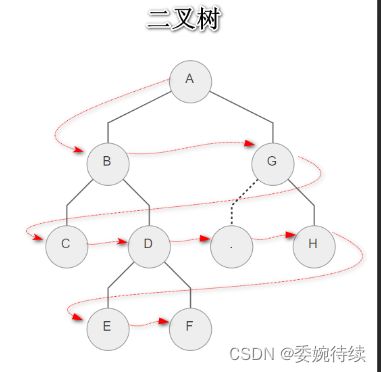
2.2.4 层序遍历

        层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层 上的节点，接着是第三层的节点，以此类推，自上而下，自左至右，逐层访问树的结点的过程就是层序遍历，其中图解如下；

                                       

2.3 前中后序代码实现（递归）

        思路：

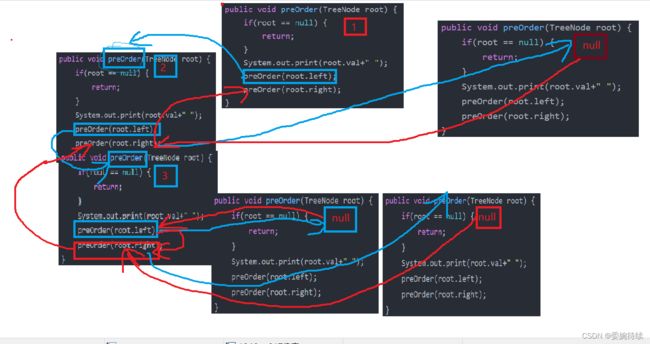
        我们将一个大的二叉树分解为一个小二叉树（由一个根节点、一个左节点、右节点构成），通过递归的思想从根节点开始依次遍历，当递归的节点为空时，我们依次按顺序退回到之前的节点，并按照不同的遍历（按照当前节点在整个树的位置）规则打印当前的节点；

                                     

2.3.1 前序遍历

// 前序遍历  根   左子树  右子树   递归
    public void preOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

        代码图解如下图所示，后面两个遍历不在画，略

2.3.2 中序遍历

    // 中序遍历
    public void inOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }

2.3.3 后序遍历

    // 后序遍历
    public void postOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val+" ");

    }

        总结：给出前序遍历与中序遍历和给出后序遍历与中序遍历可以确定一个二叉树，但是不给中序遍历或者只给一个中序遍历，是无法确定一个二叉树的

        整体代码：

import com.sun.org.apache.regexp.internal.RE;

import java.util.concurrent.Callable;

public class BinaryTree {
    static class TreeNode{
        public char value;
        public TreeNode left;
        public TreeNode right;
        public TreeNode(char value){
            this.value = value;
        }
    }
    //创建一棵二叉树 创建成功后 返回根节点A
    public TreeNode createTree(){
        TreeNode A = new TreeNode('A');
        TreeNode B = new TreeNode('B');
        TreeNode C = new TreeNode('C');
        TreeNode D = new TreeNode('D');
        TreeNode E = new TreeNode('E');
        TreeNode F = new TreeNode('F');
        TreeNode G = new TreeNode('G');
        TreeNode H = new TreeNode('H');
        A.left = B;
        A.right = C;
        B.left = D;
        B.right = E;
        C.left = F;
        C.right = G;
        E.right = H;
        return  A;
    }

    // 前序遍历  根   左子树  右子树   递归
    public void preOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        System.out.print(root.value+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

    // 中序遍历
    public void inOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.value+" ");
        inOrder(root.right);
    }

    // 后序遍历
    public void postOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.value+" ");
    }

    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        BinaryTree.TreeNode root = binaryTree.createTree();
        binaryTree.preOrder(root);
        System.out.println();
        binaryTree.inOrder(root);
        System.out.println();
        binaryTree.postOrder(root);

    }



}

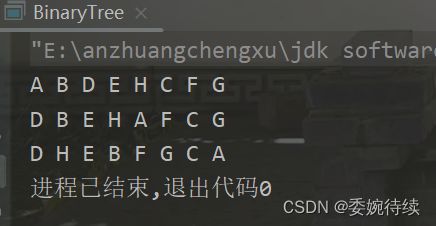
        测试结果：

 

3.二叉树的基本操作

        以下的多种操作都使用的是递归思想；

// 获取树中节点的个数
int size ( Node root );
// 获取叶子节点的个数
int getLeafNodeCount ( Node root );
// 获取第 K 层节点的个数
int getKLevelNodeCount ( Node root , int k );
// 获取二叉树的高度
int getHeight ( Node root );
// 检测值为 value 的元素是否存在
Node fifind ( Node root , int val ); 

3.1获取叶子节点的个数

        思路：

        当前节点的左右子树若都为空，说明该节点为叶子结点，返回1；树的叶子节点的个数=左树叶子节点的个数+右树叶子节点的个数

    int getLeafNodeCount(TreeNode root){
        if(root==null){
            return 0;
        }
        if(root.left==null&&root.right==null){
        return 1; 
        }
        return getLeafNodeCount(root.left)+getLeafNodeCount(root.right);
    }

3.2获取树中节点的个数 

        思路：

        若当前结点为空，返回0；先获取左节点个数，再获取右节点个数，然后返回两者相加再加上根节点的个数1

  int size(TreeNode root){
        if(root==null){
            return 0;
        }
        return size(root.right)+size(root.left)+1;
    }

3.3获取第K层节点的个数

        思路：

        依旧利用递归的思想，从树的根节点开始，每进入到树的下一层一次，令层数K-1，当k=1时，我们到达了我们要求的第k层，这样在进入到每一个下一层时，若当前节点不为空则返回1

，若为空则返回0；

        先遍历左子树k层结点，再遍历右子树k层结点，最后左子树结点加上右子树结点，就是该层结点总数

    int getKLevelNodeCount(TreeNode root, int k) {
        if(root==null){
            return 0;
        }
        if(k==1){
            return 1;
        }
        return getKLevelNodeCount(root.left,k-1)
                +getKLevelNodeCount(root.right,k-1);
    }

3.4获取二叉树的高度

        思路：

        分别统计左右子树的高度，然后进行比较，返回高度高的子树并加上根节点1；

    int getHeight(TreeNode root) {
        if(root==null){
            return 0;
        }
        int lefthight=getHeight(root.left);
        int rifhthight=getHeight(root.right);
        return lefthight>rifhthight?(lefthight+1):(rifhthight+1);
    }

3.5检测值为value的元素是否存在

        思路：

        依旧利用递归的思想，先遍历左子树，若没有找到，则返回null；若返回不为null，则返回该结点

        若左子树没有，则遍历右子树，道理相同，若最后都没找到，则返回null；

   TreeNode fifind(TreeNode root, int val) {
        if (root==null){
            return null;
        }
        if(root.val==val){
            return root;
        }
        TreeNode lefttree=fifind(root.left, val);
        if(lefttree!=null){
            return lefttree;
        }
        TreeNode righttree=fifind(root.right, val);
        if(righttree!=null){
            return righttree;
        }
        return null;
    }

ps：本次学习就到这里了，喜欢的话就请一键三连吧。