MIMO通信系统的Condition number (条件数)和 sum power gain of its eigenchannels (特征信道的总功率增益)
标题
- chatgpt的解释
- 计算的代码
- 相关论文
-
- abstract
- Introduction
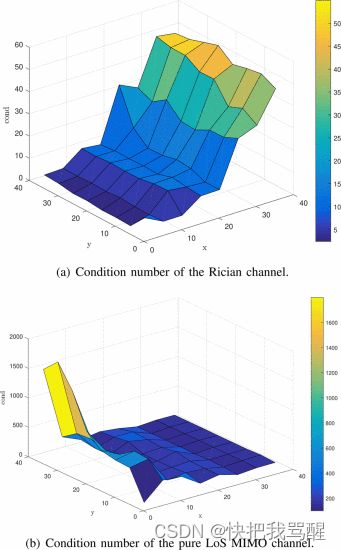
- simulation
chatgpt的解释
对于MIMO系统,如何分析其condition number and sum power gain of its eigenchannels
在 MIMO(Multiple Input Multiple Output,多输入多输出)系统中,分析条件数(condition number)和特征通道的总功率增益(sum power gain of its eigenchannels)通常涉及以下步骤:
-
矩阵表示: 将 MIMO 系统的信道矩阵表示出来。这通常是一个复杂的矩阵,其中每个元素表示从一个发射天线到一个接收天线的信道增益。
-
特征值分解: 对信道矩阵进行特征值分解。这将使你能够找到特征值和特征向量。特征值表示信道的主要特性,而特征向量表示特征通道。
-
条件数分析: 计算特征值的条件数。条件数是特征值的最大值与最小值的比率。较大的条件数通常表示系统对于输入扰动更为敏感,可能会导致数值稳定性问题。
-
总功率增益分析: 计算每个特征通道的功率增益,并将它们相加以得到总功率增益。功率增益可以通过特征值的幅度来计算。
下面是一个简化的步骤:
-
对于 MIMO 系统的信道矩阵 H,进行特征值分解: H = U Σ V H H = U \Sigma V^H H=UΣVH
其中,U 和 V 是酉矩阵,(\Sigma) 是对角矩阵,包含了信道矩阵的特征值。
-
计算条件数: Condition Number = λ max λ min \text{Condition Number} = \frac{\lambda_{\text{max}}}{\lambda_{\text{min}}} Condition Number=λminλmax
其中, λ max \lambda_{\text{max}} λmax 是特征值的最大值, λ min \lambda_{\text{min}} λmin 是特征值的最小值。 -
计算总功率增益:[ Sum Power Gain = ∑ i = 1 N ∣ λ i ∣ 2 \text{Sum Power Gain} = \sum_{i=1}^{N} |\lambda_i|^2 Sum Power Gain=∑i=1N∣λi∣2 ]
其中,N 是特征值的数量。
通过这些分析,你可以更好地了解 MIMO 系统的性能和稳定性,以及每个特征通道对总功率的贡献。这对于优化系统设计和改进通信链路的可靠性非常有用。
计算的代码
% 假设 H 是 MIMO 系统的信道矩阵
% 假设 H 是一个随机生成的 3x3 复数矩阵,实际情况根据系统大小调整
H = (randn(3) + 1i * randn(3))/sqrt(2);
% 特征值分解
[U, S, V] = svd(H);
% 条件数计算
condition_number = cond(H);
% 特征值
eigenvalues = diag(S);
% 总功率增益计算
sum_power_gain = sum(abs(eigenvalues).^2);
% 显示结果
disp('信道矩阵 H:');
disp(H);
disp('特征值分解结果:');
disp('U:'); disp(U);
disp('S:'); disp(S);
disp('V:'); disp(V);
disp(['条件数:', num2str(condition_number)]);
disp(['特征值:', num2str(eigenvalues.')]);
disp(['总功率增益:', num2str(sum_power_gain)]);
相关论文
Condition Number Improvement of IRS-Aided Near-Field MIMO Channels
@INPROCEEDINGS{10283534,
author={Huang, Wei and Lei, Bichan and He, Shiwen and Kai, Caihong and Li, Chunguo},
booktitle={2023 IEEE International Conference on Communications Workshops (ICC Workshops)},
title={Condition Number Improvement of IRS-Aided Near-Field MIMO Channels},
year={2023},
volume={},
number={},
pages={1210-1215},
doi={10.1109/ICCWorkshops57953.2023.10283534}}
abstract
在近场无线传播环境中,视距 (LoS) 链路占主导地位,这导致信号能量集中在 LoS 路径上。该文引入条件数的概念来测量多输入多输出(MIMO)系统可用的空间复用增益。通过部署新兴的智能可重构表面(IRS),给出了基于MIMO信道最小化条件数的判据,该准则通过增加反射链路和优化移相器,使信号能量均匀分布在MIMO信道的有效子信道上。然后,基于改进的MIMO信道,采用奇异值分解(SVD)方法得到最优的发射和接收波束成形矩阵,达到IRS辅助MIMO信道的容量上限。我们证明,部署 IRS 并优化其相位可以减少 MIMO 信道的条件数量,从而获得可观的多路复用增益。
Introduction
由于无线通信业务量需求的爆炸式增长,提高空间复用增益被认为是提高无线通信频谱效率的关键途径。目前,在发射机和/或接收机上配备大规模天线阵列的大规模多输入多输出(MIMO)已部署在第五代(5G)移动通信系统中[1]。为了进一步提高频谱效率,毫米波(mmWave)和太赫兹(THz)频段因其较大的可用频谱带宽而被视为5G以外移动通信系统的另一个有前途的候选者。
然而,从sub-6GHz频段到毫米波和太赫兹频段的演进导致了电磁场特性的根本变化。具体而言,由于天线数量多且载波频率高,将球面波传播近似为平面波的传统远场信道模型将不适用。对于工作在高频段的大规模MIMO通信系统,接收机将大概率驻留在瑞利距离,即近场区域。在这个区域,通道通常基于球面波假设[2]、[3]进行建模。因此,视距(LoS)链路将占主导地位,信令能量集中在LoS路径上,这导致MIMO信道的条件数增加。条件数定义为信道矩阵最大特征值与最小特征值之比,表示信道的多径丰富度,影响空间复用系统中的检测和误码性能[4],为MIMO信道的高效表征提供了深入的见解。
为了提高调理不良MIMO信道的条件数,在[5]–[7]中提出了多种收发器天线布置策略。[5]和[6]的作者最初试图优化均匀线性阵列(ULA)和均匀圆形阵列(UCA)的天线位置,以提高LoS环境中的空间复用增益。对于毫米波系统,[8]提出了两电平空间复用的概念,其中结合了路径间和路径内的隐性复用增益,并基于[7]中的几何分析结果设计了阵列空间。然而,文献[9]表明,最佳阵列/天线设计取决于传输距离和载波频率,以实现高空间复用增益。在实际通信场景中,接收机的位置始终处于动态变化状态,导致最佳阵列或天线间距随收发器的位置频繁变化。最近,在发射机和接收机之间部署智能可重构表面(IRS)已成为一种很有前途的新技术,可以扩大可实现的速率区域[10] [11]。此外,作者在文献[12]中提出了局部区域优化算法,以联合设计IRS定位和发射/反射波束成形,以提高多IRS通信系统中的系统性能。此外,IRS可以看作是人造散射器,可以在发射机和接收机之间灵活部署,通过增加可控的多径来改善条件较差的MIMO信道,而无需考虑发射机和接收机之间的距离[13]。
因此,本文利用IRS可灵活部署和调整信令能量分布的能力,研究了IRS辅助点对点近场MIMO系统的条件数改进。具体而言,MIMO信道最小化问题的条件数是在IRS相位约束下制定的,其中目标函数相对于优化变量的隐式表达式和反射相位的单位模量约束使得优化问题非凸且难以求解。为了应对这一挑战,该文结合了一些数学变换和专业化-最小化(MM)方法来解决棘手的非凸优化问题。最后,仿真结果验证了所提方法的有效性。