一级倒立摆控制 —— PID 控制器设计及 MATLAB 实现

系列文章目录

最优控制介绍
一级倒立摆控制 —— 系统建模（传递函数模型与状态空间方程表示）
一级倒立摆控制 —— 最优控制 线性二次型控制（LQR）及 MATLAB 实现
一级倒立摆控制 —— MPC 控制器设计及 MATLAB 实现
一级倒立摆控制 —— ROS2 仿真
一级倒立摆控制 —— LQR 控制器 GAZEBO 仿真

---

---

前言

在本页中，我们将为倒立摆系统设计一个 PID 控制器。在设计过程中，我们将假设一个单输入、单输出设备，其传递函数如下。除此以外，我们将尝试在不考虑小车位置的情况下控制摆的角度。

摆杆传递函数方程：
$$P_{pend}(s)=\frac{\Phi (s)}{U(s)}=\frac{\frac{ml}{q}{s}^2}{s^4+\frac{b(I+m{l}^2)}{q}{s}^3-\frac{(M+m)mgl}{q}{s}^2-\frac{bmgl}{q}s}$$
式中，$q=[(M+m)(I+m{l}^2)-(ml{)}^2]$

更具体地说，当小车受到 1-Nsec 的冲力时，控制器将试图保持摆锤垂直向上。在这些条件下，设计标准是：

1. 稳定时间小于 5 秒
2. 摆锤偏离垂直方向的幅度不应超过 0.05 弧度

有关原始问题设置和上述传递函数的推导，请查阅倒立摆： 系统建模页面。

一、系统结构

这个问题的控制器结构与您可能习惯的标准控制问题有些不同。由于我们试图控制摆的位置，而摆的位置在受到初始扰动后应返回垂直方向，因此我们跟踪的参考信号应为零。这种情况通常被称为调节器问题。施加在小车上的外力可视为脉冲干扰。该问题的示意图如下。

如果我们先将原理图重新排列如下，您可能会发现分析和设计该系统更加容易。

因此，闭环系统从力 $F$ 输入到摆角 $\varphi$ 输出的传递函数 $T(s)$ 确定如下。

$$\begin{array}{c}T(s)=\frac{\Phi (s)}{U(s)}=\frac{P_{pend}(s)}{1+C(s)P_{pend}(s)}\end{array}$$

在开始设计 PID 控制器之前，我们首先需要在 MATLAB 中定义倒立摆传递函数模型。创建一个新的 .m 文件并键入以下命令来创建传递函数模型（有关获取这些命令的详细信息，请参阅主问题）。

M = 0.5;
m = 0.2;
b = 0.1;
I = 0.006;
g = 9.8;
l = 0.3;
q = (M+m)*(I+m*l^2)-(m*l)^2;
s = tf('s');
P_pend = (m*l*s/q)/(s^3 + (b*(I + m*l^2))*s^2/q - ((M + m)*m*g*l)*s/q - b*m*g*l/q);

接下来，我们将定义一个 PID 控制器。

二、PID 控制

在 MATLAB 中可以通过将以下代码复制到 .m 文件末尾来模拟闭环传递函数（无论您使用的是传递函数形式还是模型的状态空间表示形式）。具体来说，我们使用 MATLAB 中的 pid 对象定义控制器。然后，我们使用反馈命令生成闭环传递函数 $T(s)$，如上图所示，其中干扰力 $F$ 为输入，摆锤角度与垂直方向的偏差 $\varphi$ 为输出。

t=0:0.01:10;
impulse(T,t)
title({'Response of Pendulum Position to an Impulse Disturbance';'under PID Control: Kp = 1, Ki = 1, Kd = 1'});

这个响应仍然不稳定。让我们开始通过增加比例增益来修改响应。增加 $K_p$ 变量，看看它对响应有什么影响。如果将 .m 文件修改为 $K_p$ = 100，并在命令窗口中运行，将得到下图所示的响应图。

Kp = 100;
Ki = 1;
Kd = 1;
C = pid(Kp,Ki,Kd);
T = feedback(P_pend,C);
t=0:0.01:10;
impulse(T,t)
axis([0, 2.5, -0.2, 0.2]);
title({'Response of Pendulum Position to an Impulse Disturbance';'under PID Control: Kp = 100, Ki = 1, Kd = 1'});

在绘制的曲线图上单击右键，从菜单中选择 “特征”，即可确定响应的重要特征。具体来说，响应的稳定时间被确定为 1.64 秒，小于 5 秒的要求。由于稳态误差以足够快的速度趋近于零，因此不需要额外的积分动作。您可以将积分增益常数 $K_i$ 设为零，以亲自验证是否需要进行积分控制。不过，峰值响应大于 0.05 弧度的要求。回想一下，通常可以通过增加导数控制量来减少过冲。经过反复试验，我们发现导数增益 $K_d$ = 20 可以提供令人满意的响应。对 m 文件作如下修改并重新运行后，将得到下图所示的响应图

Kp = 100;
Ki = 1;
Kd = 20;
C = pid(Kp,Ki,Kd);
T = feedback(P_pend,C);
t=0:0.01:10;
impulse(T,t)
axis([0, 2.5, -0.2, 0.2]);
title({'Response of Pendulum Position to an Impulse Disturbance';'under PID Control: Kp = 100, Ki = 1, Kd = 20'});

可以看到，过冲已经减小，摆锤偏离垂直方向的幅度不会超过 0.05 弧度。由于所有给定的设计要求都已满足，因此不需要进一步迭代。

三、小车的位置会发生什么变化？

本页开头给出了倒立摆系统的方框图。该图并不完整。代表小车位置 $x$ 响应的图块没有包括在内，因为该变量没有被控制。但有趣的是，当摆锤角度 $\varphi$ 的控制器就位时，小车的位置会发生什么变化。要了解这一点，我们需要考虑整个系统框图，如下图所示。

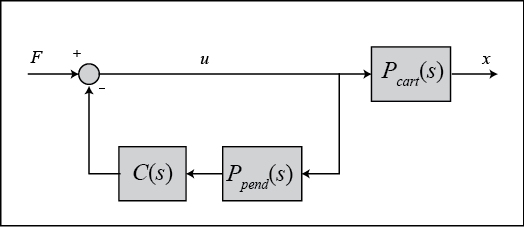
重新排列后，我们得到以下框图。

在上图中，块$C(s)$ 是为保持摆锤垂直而设计的控制器。因此，从施加到小车的输入力到小车位置输出的闭环传递函数 $T_2(s)$ 如下所示。

$$\begin{array}{c}T(s)=\frac{X(s)}{F(s)}=\frac{P_{cart}(s)}{1+C(s)P_{pend}(s)}\end{array}$$

请参考倒立摆： 系统建模页面，$P_{cart}(s)$ 的传递函数定义如下。

$$\begin{array}{c}{P}_{cart}(s)=\frac{\Phi (s)}{U(s)}=\frac{\frac{(I+m{l}^2)s^2-mgl}{q}}{s^4+\frac{b(I+m{l}^2)}{q}{s}^3-\frac{(M+m)mgl}{q}{s}^2-\frac{bmgl}{q}s}\end{array}$$

式中，$q=[(M+m)(I+m{l}^2)-(ml{)}^2]$

在您的 m 文件中添加以下命令（假设 $P_{pend}(s)$ 和 $C(s)$ 仍已定义），将生成小车位置对我们一直在考虑的相同脉冲干扰的响应。

P_cart = (((I+m*l^2)/q)*s^2 - (m*g*l/q))/(s^4 + (b*(I + m*l^2))*s^3/q - ((M + m)*m*g*l)*s^2/q - b*m*g*l*s/q);
T2 = feedback(1,P_pend*C)*P_cart;
t = 0:0.01:5;
impulse(T2, t);
title({'Response of Cart Position to an Impulse Disturbance';'under PID Control: Kp = 100, Ki = 1, Kd = 20'});

可以看到，小车以近似恒定的速度向负方向移动。因此，尽管 PID 控制器能稳定摆锤的角度，但在实际物理系统中实施这种设计并不可行。

---