LeetCode 每日一题 Day 10 || 并查集/二分搜索

1631. 最小体力消耗路径

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

示例 1：

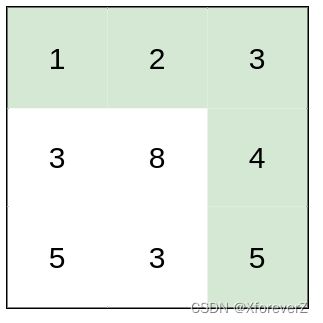
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10⁶

这个题目第一眼看到就想DFS+二分,后面看了题解之后尝试了并查集来实现，但是代码似乎有点臃肿，时间和空间开销都比较大，首先讲一下我的第一种解法，二分搜索：

class Solution
{
public:
    bool dfs(const vector<vector<int>> &heights, int mid, int row, int col, vector<vector<bool>> &visited)
    {
        int row = heights.size();
        int col = heights[0].size();
        // 达到终点
        if (row == row - 1 && col == col - 1)
        {
            return true;
        }
        // 标记当前位置已访问

        visited[row][col] = true;
        // 定义四个方向的坐标变化

        vector<pair<int, int>> direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        for (const auto &dir : direction)
        {
            int newRow = row + dir.first;
            int newCol = col + dir.second;

            // 检查新位置是否合法
            if (newRow >= 0 && newRow < row && newCol >= 0 && newCol < col &&
                !visited[newRow][newCol] && abs(heights[newRow][newCol] - heights[row][col]) <= mid)
            {
                if (dfs(heights, mid, newRow, newCol, visited))
                {
                    return true;
                }
            }
        }

        return false;
    }
    int minimumEffortPath(vector<vector<int>> &heights)
    {
        int left = 0, right = 1e6;

        while (left < right)
        {
            int mid = left + (right - left) / 2;

            vector<vector<bool>> visited(heights.size(), vector<bool>(heights[0].size(), false));

            if (dfs(heights, mid, 0, 0, visited))
            {
                // 如果可以达到终点，尝试减小体力值
                right = mid;
            }
            else
            {
                // 如果无法达到终点，增大体力值
                left = mid + 1;
            }
        }

        return left;
    }
};

下面是看了官方题解之后的并查集代码：

class UnionFind
{
public:
    vector<int> parent;
    vector<int> rank;

    UnionFind(int size)
    {
        parent.resize(size);
        rank.resize(size, 1);

        // 初始化并查集，每个节点的父节点为自己
        for (int i = 0; i < size; ++i)
        {
            parent[i] = i;
        }
    }

    // 查找节点所属集合的根节点
    int find(int x)
    {
        if (parent[x] != x)
        {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    // 合并两个集合
    void unite(int x, int y)
    {
        int rootX = find(x);
        int rootY = find(y);

        if (rootX != rootY)
        {
            if (rank[rootX] > rank[rootY])
            {
                parent[rootY] = rootX;
            }
            else if (rank[rootX] < rank[rootY])
            {
                parent[rootX] = rootY;
            }
            else
            {
                parent[rootY] = rootX;
                rank[rootX]++;
            }
        }
    }
};
class Solution
{
public:
    int minimumEffortPath(vector<vector<int>> &heights)
    {
        int rows = heights.size();
        int columns = heights[0].size();

        // 存储边的格式为 {体力消耗值, 单元格1, 单元格2}
        vector<vector<int>> edges;

        // 根据相邻单元格的高度差构建边
        for (int row = 0; row < rows; ++row)
        {
            for (int col = 0; col < columns; ++col)
            {
                if (row > 0)
                {
                    edges.push_back({abs(heights[row][col] - heights[row - 1][col]), row * columns + col, (row - 1) * columns + col});
                }
                if (col > 0)
                {
                    edges.push_back({abs(heights[row][col] - heights[row][col - 1]), row * columns + col, row * columns + col - 1});
                }
            }
        }

        // 根据体力消耗值升序排序边
        sort(edges.begin(), edges.end(), [](const vector<int> &a, const vector<int> &b)
             { return a[0] < b[0]; });

        UnionFind uf(rows * columns);

        // 遍历排序后的边，使用并查集找到最小体力消耗值
        for (const vector<int> &edge : edges)
        {
            uf.unite(edge[1], edge[2]);
            if (uf.find(0) == uf.find(rows * columns - 1))
            {
                return edge[0];
            }
        }

        return 0;
    }
};