python算法
算法的五大特性
- 输入 : 算法具有0个或多个输入
- 输出 : 算法至少有1个或多个输出
- 有穷性 : 算法在有限的步骤之后会自动结束而不会无限循环, 并且每一个步骤可以在可接受的时间内完成
- 确定性: 算法中的每一步都有确定的含义, 不会出现二义性
- 可行性 : 算法的每一步都是可行的, 也就是说每一步都能够执行有限的次数完成
算法效率的描述
基本运算总数*基本运算耗时 ~= 运行时间
基本运算函数 —>渐进函数
O(n) -------> n问题规模
时间复杂度的几条基本计算规则
- 基本操作, 即只有常数项, 认为其时间复杂度为O(1)
- 顺序结构, 时间复杂度按加法进行计算
- 循环结构, 时间复杂度按乘法进行计算
- 分支结构, 时间复杂度取最大值
- 判断一个算法的效率时,往往只需要关注操作数量的最高次项,其他次要项和常数项可以忽略
- 在没有特殊说明时, 我们所分析的算法的事件复杂度都是指最坏时间复杂度
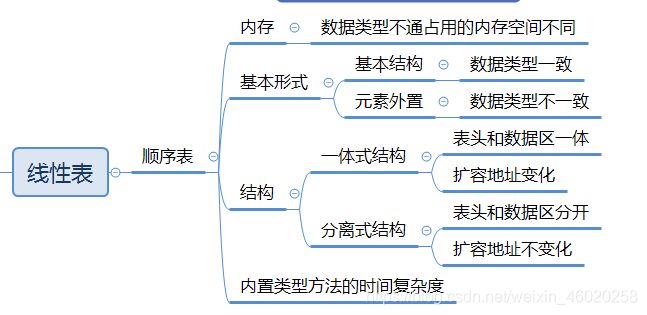
时间复杂度所消耗的时间 timeit模块 class timeit.Timer(stmt=‘pass’, setup=‘pass’, timer=) timer 是测量一小段代码执行速度的类. timer.Timer.timeit(number = 1000000) 默认为100w次 图b这样的顺序表也被称为对实际数据的索引,这是最简单的索引结构 一体式结构,存储表信息的单元与元素存储区以连续的方式安排在一块存储区里, 两部分数据的整体形成一个完整的顺序表对象. 一体式结构整体性强, 易于管理. 但是由于数据元素存储区域是表对象的一部分, 顺序表创建后, 元素存储区就固定了. 链表 单向链表 表元素域elem 用来存放具体的数据. 双向链表结构 一种更复杂的链表是"双向链表" 或 “双面链表”. 每个节点有两个链接: 一个指向前一个节点, 当此节点为第一个节点时, 指向空值; 而另一个指向下一个节点, 当此节点为最后一个节点时, 指向空值. 数据结构与算法 冒泡排序(背下来) 比较相邻的元素. 如果第一个比第二个大(升序), 就交换他们两个。 时间复杂度 选择排序 选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,他们当中至少有一个将被移到其最终位置上,因此对n个元素的表进行排序总共进行至多n-1此交换。在所有的完全依靠交换去移动元素的排序方法中,算则排序属于非常好的一种。 时间复杂度 插入排序 时间复杂度 希尔排序 时间复杂度 快速排序(背下来) 步骤为: 递归地最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把衣蛾元素摆到它最后的位置去。 时间复杂度 归并排序 将数组分解最小之后,然后葛冰两个有序数组,基本思路是比较两个数组的最前面的书,谁小就先取谁,取了后相应的指针就往后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来既可。 时间复杂度 搜索 常见的几种方法:顺序查找、二分法查找、二叉树查找、哈希查找 二分法查找 树与树算法 树是一种抽象数据类型(ADT)或是实作这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一颗倒挂的树,也就是说它是根朝上,而叶朝下的。它具有一下的特点: 每个节点有零个或多个子节点; 森林:有m(m》=0)颗互不相交的树的集合称为森林。 树的存储与表示 常见的一些树的应用场景 二叉树 二叉树的基本概念 二叉树的性质(特性) 性质1:在二叉树的第i层上至多有2^(i-1)个节点(i>0) 二叉树的遍历 那么深度遍历有重要的三种方法。这三种方式常被用于访问树的节点,它们之间的不同在于访问每个节点的次序不同。这三种遍历分别叫做先序遍历(preorder),中序遍历(inorder)和后序遍历(postorder)。 先序遍历 中序遍历 后序遍历 广度优先遍历(层次遍历)
O(1)
stmt 参数是要测试的代码语句(statment) ;
setup 参数是运行代码时需要的设置;
timer 参数是一个定时器函数, 与平台有关
分离式结构,表对象里只保存与整个表有关的信息(即容量和元素个数), 实际数据元素存放在另一个独立的元素存储区里, 通过链接与基本表对象关联.
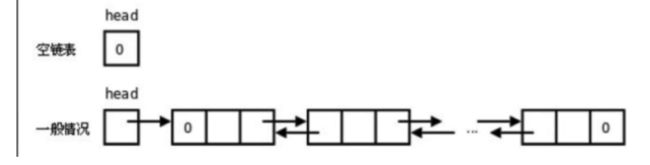
链表定义
链表是一种常见的基础数据结构, 是一种线性表, 但是不像顺序表一样连续存储数据, 而是在每一个节点 (数据存储单元) 里存放下一个节点的位置信息 (即地址) .
单向链表也叫单链表, 是链表中最简单的一种形式, 它的每个节点包含两个域, 一个信息域(元素域)和 一个链接域. 这个链接指向链表中的下一个节点, 而最后一个节点的链接域则指向一个空值.

链接域next 用来存放下一个节点的位置(python中的标识)
变量p 指向链表的头节点(首节点)的位置, 从p出发能找到表中的任意节点.
对每一对相邻元素作同样的工作, 从开始第一队到结尾的最后一对. 这步做完后, 最后的元素会是最大的数。
针对所有的元素重复以上的步骤,,除了最后一个。
持续每次对越来越少的元素重复上面的步骤, 直到没有任何一堆数字需要比较。
最优时间复杂度 :O(n)
平均时间复杂度 O(n^2)
最坏时间复杂度 :O(n^2)
稳定性 :不稳定
备注 :n小时比较好
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,在从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
最优时间复杂度 :O(n^2)
平均时间复杂度 :O(n^2)
最坏时间复杂度 :O(n^2)
稳定性 :不稳定
备注 :n小时比较好
它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,在从后向前扫描过程中,需要反复把已排序元素逐步向厚挪威,为最新元素提供插入空间。
最优时间复杂度 :O(n)
平均时间复杂度 :O(n^2)
最坏时间复杂度 :O(n^2)
稳定性 :稳定
备注 :大部分已有序时好
希尔排序也是插入排序的一种。也称缩小增量排序,是直接插入算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL. Shell于1959年提出而得名。希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量主键减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被纷争一组,算法便终止。
最优时间复杂度 :O(nlogn)
平均时间复杂度 :O(nlogn)~O(n^2)
最坏时间复杂度 :O(n^2)
稳定性 :不稳定
备注 :和步长有关
又称划分交换排序,通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,一次达到整个数据变成有序序列。
1.从数列中挑出一个元素,成为“基准”(pivot)
2。重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任意一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
3.递归地(recursive) 把小于基准值元素的子数列和大于基准值元素的子数列排序。
最优时间复杂度 :O(nlogn)
平均时间复杂度 :O(nlogn)
最坏时间复杂度 :O(n^2)
稳定性 :不稳定
备注 :n大时比较好
归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分组数组,再合并数组。
最优时间复杂度 :O(nlogn)
平均时间复杂度 :O(nlogn)
最坏时间复杂度 :O(nlogn)
稳定性 :稳定
备注 :n大时比较好
二分法查找又称折半查找,有点事比较次数少,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。
没有父节点的节点称为根节点;
每一个非根节点有且只有一个父节点;
除了根节点外,每个字节点可以分为多个不想交的子树;
二叉树是每个节点最多有讲个子树的树结构。通常子树被称作“左子树”和“右子树”
性质2:胜读为k的二叉树至多有2^k-1个节点(k>0)
性质3:对于任意一颗二叉树,如果其叶节点树为N0,而度数为2的节点总数为N2,则N0=N2+1;
性质4:具有n个节点的完全二叉树的深度必为log2(n+1)
性质5:对完全二叉树,若从上至下、从左至右编号,则编号为i的节点,其左孩子编号必为2i,其右孩子编号必为2i + 1;其双亲的编号必为i/2(i=1时为根,除外)
树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的信息的访问,即依次对树中每个结点访问一次且仅访问一次,我们把这种对所有节点的访问称为遍历(traversal)。那么树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先一般用递归,广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。
在先序遍历中,我们先访问根节点,然后递归使用先序遍历访问左子树,再递归使用先序遍历访问右子树
在中序遍历中,我们递归使用中序遍历访问左子树,然后访问根节点,最后再递归使用中序遍历访问右子树
在后序遍历中,我们先递归使用后序遍历访问左子树和右子树,最后访问根节点
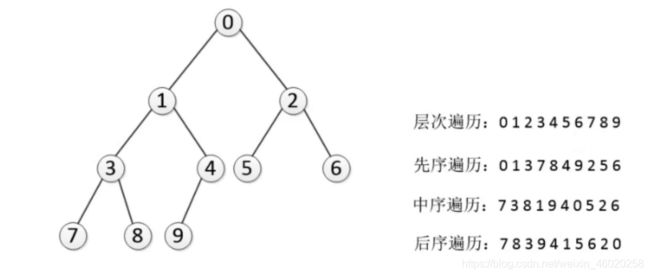
从树的root开始,从上到下,从左到右遍历整个树的节点