常见注意力机制原理介绍与对比

1. 引言

    自从2014年Seq2Seq提出以来，神经机器翻译取得了很多的进展，但是大部分模型都是基于encoder-decoder的结构，这就要求encoder对于输入序列的编码能力要足够强，才能确保得到的输入序列的上下文向量能够尽可能地保留输入序列的信息。而我们知道，随着句子的长度逐渐变长，上下文向量的表达能力其实是会逐渐下降的，因为它没法完全保留输入序列的大部分信息。因此，为了克服这个问题，使得encoder-decoder结构也能应付长序列，很多学者开始寻求各种解决方法，其中，主流的就是采用注意力机制，即在decoder时不再只考虑encoder的最后一个时间步的隐藏状态，而是在decoder的每个时间步时，能够自动地从输入序列的所有时刻的隐藏状态列表中自动搜索与当前输出目标最相关的一些隐藏状态，然后将这些隐藏状态与decoder前面时刻的输出一起作为decoder当前时刻的输入，下面我们将介绍几种主流的注意力机制，并将它们进行对比。

• Bahdanau Attention：《NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE》
• Luong Attention：《Effective Approaches to Attention-based Neural Machine Translation》

2. 常见的注意力机制

2.1 Bahdanau Attention

    Bahdanau Attention是由Bahdanau等人在2015年提出来的一种注意力机制。其结构还是采用encoder-decoder形式，如图1所示。

图1 Bahdanau Attention模型结构

    在encoder层，Bahdanau Attention采用的是BiRNN的结构，其中，RNN采用GRU单元，记输入序列和输出序列分别为：

                                                         

                                                         

其中，和分别表示输入和输出序列的词汇量大小，和分别表示输入和输出序列的长度。则对于BiRNN的前向过程，隐藏状态的计算公式如下：

                                                         

                                                         

其中，表示更新门，用于确定上一步的隐藏状态有多少信息要保留到下一步，表示遗忘门，用于遗忘上一步的隐藏状态的一些不重要的信息，表示元素乘积操作，表示输入序列的词向量矩阵，表示词向量的维度，为权重矩阵，也是权重矩阵，表示隐藏层的维度，是sigmoid函数。经过前向过程后，将得到每个时间步的隐藏状态，记为，同理，BiRNN的反向过程的计算逻辑也是一样的，这里不再赘述，记反向过程得到的每个时间步的隐藏状态为。Bahdanau Attention将各个时刻前向和后向的隐藏状态进行拼接作为每个时刻的输出，记拼接后的隐藏状态为，则其计算公式如下：

                                                         

这样一来，每个时间的隐藏状态不仅包括了该时刻的输入信息，也包括该时刻前面和后面的序列信息。

    在decoder层，Bahdanau Attention计算每个时间步的隐藏状态如下：

                                                        

                                                        

其中，表示目标输出的词向量，均为权重矩阵，分别对应词向量和隐藏层的维度，另外，对于初始隐藏状态，采用encoder中第一个时间步的反向过程的隐藏状态进行计算，其计算公式如下：

                                                        

其中，。可以发现，其实decoder的计算过程与encoder的计算过程非常相似，只是多了一项输入，即，这里表示输入序列的上下文向量，但是与传统的encoder-decoder不一样的地方的这个上下文向量是随着而变化的，当时，则与传统的encoder-decoder方法一致。那么，对于Bahdanau Attention中的，其计算公式是这样的：

                                                       

其中，表示输入序列的长度，表示encoder第j个时间步的隐藏状态，表示的权重，其计算公式如下：

                                                         

                                                        

其中，表示decoder前一个时间步的隐藏状态，为权重矩阵，可以发现，Bahdanau Attention在decoder的每个时刻，会对encoder的所有时间步的隐藏状态进行加权平均作为当前时刻的上下文向量，这样一来，使得在decoder的每个时间步都能重点关注与该时间步最相关的一些输入信息，如图2所示，表示输入序列和输出序列的权重分布图，可以发现每个输出词汇都会重点关注与其最相关的输入词汇，从而提高decoder的准确率。

图2 权重热力图

 

    最后，将decoder每个时间步的隐藏状态经过一个带有relu激活函数和softmax函数即可得到当前时刻目标输出的概率分布：

                                                         

以上就是Bahdanau Attention的整个计算逻辑，该注意力机制克服了传统encoder-decoder在长序列表现差的缺点。

2.2 Luong Attention

    Luong Attention也是在2015年由Luong提出来的一种注意力机制。Luong在论文中提出了两种类型的注意力机制：一种是全局注意力模型，即每次计算上下文向量时都考虑输入序列的所有隐藏状态；另一种是局部注意力模型，即每次计算上下文向量时只考虑输入序列隐藏状态中的一个子集。

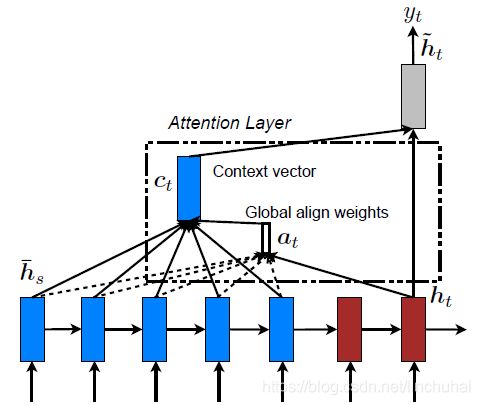
    Luong Attention的模型结构也是采用encoder-decoder的形式，只是在encoder和decoder中，均采用多层LSTM的形式，如图3所示。对于全局注意力模型和局部注意力模型，在计算上下文向量时，均使用encoder和decoder最顶层的LSTM的隐藏状态。

图3 Luong Attention模型结构

2.2.1 全局注意力模型

    全局注意力模式在计算decoder的每个时间步的上下文向量时，均考虑encoder的所有隐藏状态，记每个时间步对应的权重向量为，其计算公式如下：

                                                         

其中，表示当前decoder第个时间步的隐藏状态，表示encoder第个时间步的隐藏状态，这里与Bahdanau Attention不同的是在计算权重时，采用的是decoder当前时刻的隐藏状态，而不是上一时刻的隐藏状态，即attention是在decoder中LSTM层之后的，而Bahdanau Attention的attention则是在decoder的LSTM层之前的，换句话说，全局注意力模型的计算路径是，而Bahdanau的计算路径是。另外，Luong Attention在计算权重时提供了三种计算方式：

                                                         

其中，concat模式跟Bahdanau Attention的计算方式一致，而dot和general则直接采用矩阵乘积的形式。在计算完权重向量后，将其对encoder的隐藏状态进行加权平均得到此刻的上下文向量，然后Luong Attention将其与decoder此刻的隐藏状态进行拼接，并通过一个带有tanh的全连接层得到，其计算公式如下：

                                                         

    最后，将传入带有softmax的输出层即可得到此刻目标词汇的概率分布，其计算公式如下：

                                                        

    全局注意力模型的结构如图4所示，作者在实验时也发现，对于全局注意力模型，采用dot的权重计算方式效果要更好。

图4 全局注意力模型

2.2.2 局部注意力模型

     然而，全局注意力模型由于在每次decoder时，均考虑encoder所有的隐藏状态，因此，其计算成本是非常昂贵的，特别是对于一些长句子或长篇文档，其计算就变得不切实际，因此，作者又提出了另一种注意力模式，即局部注意力模型，即每次decoder时不再考虑encoder的全部隐藏状态了，只考虑局部的隐藏状态。

    在局部注意力模型中，在decoder的每个时间步，需要先确定输入序列中与该时刻对齐的一个位置，然后以该位置为中心，设定一个窗口大小，即，其中是一个整数，用来衡量窗口的大小，具体的取值需要凭经验设定，作者在论文中设定的是10，接着，在计算权重向量时，只考虑encoder中在该窗口内的隐藏状态，当窗口的范围超过输入序列的范围时，则对超出的部分直接舍弃。局部注意力模型的计算逻辑如图5所示。

图5 局部注意力模型

    在确定位置时，作者也提出了两种对齐方式，一种是单调对齐，一种是预测对齐，分别定义如下：

• 单调对齐（local-m）：即直接设定，该对齐方式假设输入序列与输出序列的按时间顺序对齐的，接着计算的方式与全局注意力模型相同。
• 预测对齐（local-p）：预测对齐在每个时间步时会对进行预测，其计算公式如下：
                                
                                                    
  
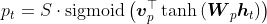
  其中，和均值权重矩阵，为输入序列的长度，这样一来，。另外，在计算时，作者对还采用了一个高斯分布进行修正，其计算公式如下：
  
                                                   
  
  其中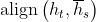，与全局注意力模型的计算公式相同，表示输入序列的位置，。

     计算完权重向量后，后面上下文向量、以及概率分布的计算都与全局注意力模型的计算方式相同，这里不再赘述。作者在实验中发现，局部注意力模型采用local-p的对齐方式往往效果更好，因为在真实场景中，输入序列和输出序列往往的没有严格单调对齐的，比如在翻译任务中，往往两种语言在表述同样一种意思时，其语序是不一致的。另外，计算权重向量的方式采用general的方式效果比较好。

2.2.3 Input-feeding方法

     在论文中，作者还提及了一个技巧——Input-feeding，即在decoder时，前面的词汇的对齐过程往往对后续词汇的对齐和预测是有帮助的，那么，如何将前面的对齐信息传递给后面的预测，作者提出了一个很简单的技巧，即把上一个时刻的与下一个时刻的输入进行拼接，一起作为下一个时刻的输入。作者在实验时发现这样一个技巧可以显著提高decoder的效果。但是这样的操作对encoder和decoder第一层的LSTM就有一个要求，假设顶层LSTM的隐藏单元数量都设置为，那么，采用Input-feeding后，就要求encoder和decoder第一层的LSTM的隐藏单元数量都为，因为拼接操作会使得输入向量的长度翻倍，如图6所示。

图6 Input-feeding方法

    以上就是Luong Attention的原理啦，其实就是对Bahdanau Attention的一种推广，两者在思路方面还是很多相似的。 

3. 总结

    上面介绍了注意力机制中的常见形式，其实注意力机制还有很多种变式，不过感觉都差不多，最后大致做一个总结吧：

• Bahdanau Attention的权重计算采用的是一种加法的形式，attention层在decoder的LSTM层之前完成，但是每次计算时都考虑encoder的全部隐藏状态，计算开销比较大。
• Luong Attention则对权重的计算方式进行了推广，提供了三种计算方式，并且在计算上下文向量时提供了全局和局部两种模式，特别是局部注意力模式，在计算速度上要快得多，更加适合长句子或长文档。另外，其attention层是在decoder的LSTM层之后完成。