数学模型-层次分析法
目录
前言
计算步骤
模型的建立
正互反矩阵
一致性指标和一致性检验
一致性指标
随机一致性指标
一致性比率
一致矩阵
综合权重
简单例题
综合例题
前言
层次分析法（Analytic Hierarchy Process，AHP）是一种决策分析工具，由美国数学家托马斯·L. 萨蒂（Thomas L. Saaty）于1970年发明。该方法运用了数学、心理学和管理学的基本原理，旨在帮助人们更好地进行多准则决策。AHP方法包括构建层次结构模型、建立判断矩阵、计算权重和一致性指标、进行结果分析等步骤。它的基本思想是通过比较不同元素之间的相对重要性，从而得出最终的决策。AHP方法在许多领域应用广泛，如投资决策、市场营销、工程管理、环境评估等。
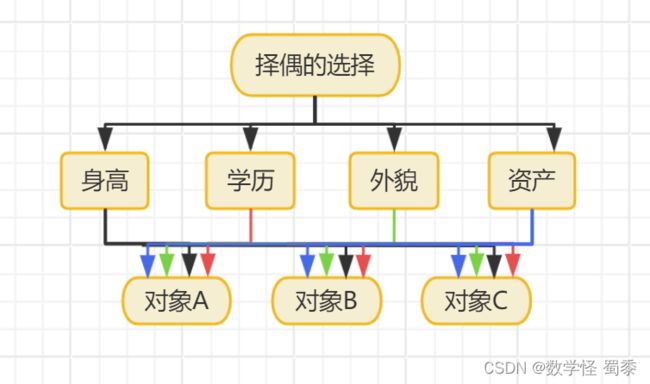
理论太多，直接来点实际问题，比如有三个对象同时追你
对象A家产富裕，但是身高外貌学历可能一般般
对象B家产一般般，身高外貌学历也是一般般
对象C家产并不富裕，但是身高外貌学历非常优秀。
这时候你该如何选择？
计算步骤
模型的建立
将决策的目标、考虑的因素（决策准则）和决策对象按它们之间的相互关系分为最高层、中间层和最低层，绘出层次结构图。
最高层是指决策的目的、要解决的问题。
最低层是指决策时的备选方案。
中间层是指考虑的因素、决策的准则。
对于相邻的两层，称高层为目标层，低层为因素层。
正互反矩阵
即
例如下面这个矩阵。
（X1身高，X2学历，X3外貌，X4资产）
该矩阵内的每一个元素代表决策者对择偶的选择重要性来说，
比如
代表身高X1与学历X2的重要程度之比，顾名思义就是决策者认为学历比身高稍微重要一些。
再看
代表学历X2与身高X1的重要程度之比，顾名思义就是决策者认为学历比身高稍微重要一些。
接下来就是把四个元素（身高、学历、外貌、资产）进行两两比较。n(n-1)/2=3+2+1
根据决策者自己觉得的重要程度之比
即可得到矩阵的上三角元素。上三角元素出来了，下三角也易知。
之后你可能会发现，，
，那么理论上来说X1:X3应该是1：4
但A矩阵里面的
，和实际的1/4并没有达成一致性
因此我们需要对A矩阵不一致的范围加以界定。
所以一致性指标和一致性检验的概念就出现了
一致性指标和一致性检验
一致性指标
（
为A的最大特征值，n为阶数）
CI越大说明一致性越差。
CI越接近0说明是满意的一致性。
随机一致性指标
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|
| RI | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
Saaty给出的随机一致性指标RI的数值
一致性比率
当CR小于0.1时，说明通过一致性检验
当大于等于0.1时，说明不通过一致性检验，需要回去重新对矩阵进行调整。
假设A矩阵已经通过一致性检验，那么A最大特征值对应的特征向量可以作为权向量。
所以对于前面的A矩阵。
,n=4,CI算的0.0035
又由RI数值表知RI=0.90.所以CR算的0.0039＜0.1，故通过一致性检验。
通过一致性检验，归一化的特征向量（权向量）就出来了
权向量有了，接下来就是计算综合权重的问题。
在此之前需要先引入一致矩阵的概念。
一致矩阵
可以看出每一行都成比例，所以可以化成
即秩为1.
容易看出该矩阵的性质：
G的秩为1，唯一非零特征根为n，任何一列向量都是对应于特征根n的特征向量。
总结：
综合权重
前面我们已经算出来了第二层（准则层）对第一层（目标层）的权重。
接下来我们用同样的方法确定第三层（方案层）对第二层每一准则的权重。
二层对一层，二层四个元素，一层一个元素，即构成一个四乘四的矩阵
三层对二层，三层三个元素，二层四个元素，即构成四个三乘三的矩阵。
即
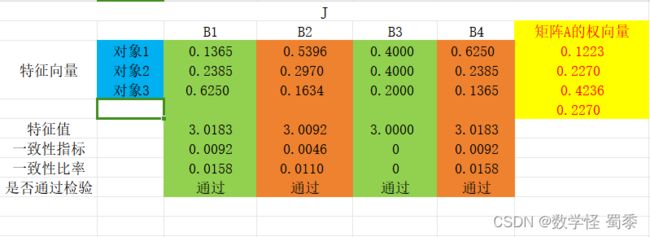
易看出只有B3为一致阵。其他三个需要进行一致性检验。
第三行的数值。即B1~B4下面那一行，分别是对象1对四项准则的权重。
所以把他们与矩阵A的权向量相乘，即可得到对象1对目标层的权重。
对象2、对象3也类似可以得到。
所以综合权重W=（对象1xA权向量，对象2xA权向量，对象3xA权向量）
用matlab计算得W=(0.4505,0.3202,0.2292)^T
即三位对象排名为对象1、对象2、对象3
简单例题
这题直接一眼看穿，任意两行构成比例，即为一致矩阵，易知可通过检验
=3,所以随便一列归一化计算即可得到权向量。
咱们拿第一列出来,即权向量为W=(w1,w2,w3)
w1=1/(1+0.5+0.6667)=0.5455
w2=0.5/(1+0.5+0.6667)=0.2727
w3=0.6667/(1+0.5+0.6667)=0.1818
所以W=(0.5455,0.2727,0.1818)
这题也是直接一眼看穿，任意两行构成比例，即为一致矩阵，易知可通过检验
=3,所以随便一列归一化计算即可得到权向量。
咱们拿第一列出来,即权向量为W=(w1,w2,w3)
w1=1/(1+0.5+0.25)=0.5714
w2=0.5/(1+0.5+0.25)=0.2857
w3=0.25/(1+0.5+0.25)=0.1428
所以W=(0.5714,0.2857,0.1428）
综合例题
（1）四项标准在某君心目中的重要性即二层（准则层）对一层（目标层）的 权重。
题中给出A矩阵最大特征值对应的特征向量为（0.5820，0.2786，0.0899，0.0495）
所以心目中的重要性C1>C2>C3>C4.
即待遇>离家近远>晋升机会>工作环境。
（2）
即重要程度b>a>c.
a=40.91%
b=44.16%
c=14.93%