部分常用算法笔记
一、简单易考
1、冒泡排序
https://www.nowcoder.com/practice/2baf799ea0594abd974d37139de27896
for i:=0;i
array[j+1],array[j] = array[j],array[j+1]
}
}
}
2、求数组最大最小值。
1)O(N)
max := arr[0]
for i := 1; i < len(arr); i++ {
if arr[i] > max {
max = arr[i]
}
}
2) 最小栈
https://leetcode.cn/problems/min-stack/
3、实现getElementById
var elements = document.getElementsByTagName(“*”);
for (var i = 0; i < elements.length; i++) {
if (elements[i].id === id) {
return elements[i];
}
}
4、二分法
https://www.nowcoder.com/practice/d3df40bd23594118b57554129cadf47b
二、题
1、反射
value := reflect.ValueOf(&animal)
f := value.MethodByName(“Eat”)
//f.Call([]reflect.Value{})
reflect.DeepEqual()
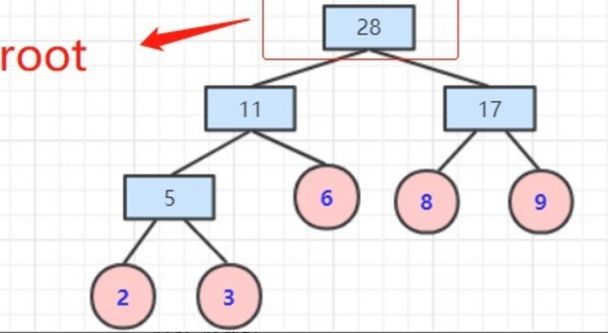
带权路径长度WPL为:23+33+62+82+9*2=(2+3)*3+(6+8+9)*2=61.
3、排序
Q: 稳定排序算法?
稳定不稳定就看相同的关键字在排序前后的次序是否发生变化.
稳定的有:冒泡排序、插入排序、归并排序;不稳定的有选择排序、快速排序、堆排序和希尔排序。
冒泡排序:重复地走访过要排序的元素列,依次比较两个相邻的元素,如果他们的顺序错误就把他们交换过来。
归并排序:将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
插入排序:将待排序序列分成两个序列,前面的序列保持有序,依次选取后面的序列的元素,在前面的序列中进行插入。初始时,有序序列的长度为1。
快速排序:快速排序是指通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序。
堆排序:堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
希尔排序:希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。在小规模数据或者基本有序的数据上使用时十分高效。
4、二叉树
深度为n,最大节点数:(2n)-1个节点。第n层,每层最大节点数:2(n-1)。
n个节点,最大深度为[logN]+1
完全二叉树:最后一层没有满,那么最后一层的节点都得在左边。满二叉树是特殊的完全二叉树。对于满二叉树,除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。
5、红黑树(RBTree)
红黑树是一种特定类型的二叉树。
性质:
根节点是黑色的
每个红色结点的两个子结点都是黑色
对于每个节点,从该节点到其后代叶节点的简单路径上,均包含相同数目的黑色节点
每个叶子节点都是NIL,颜色为黑色
通俗理解:算法实现时,每次假定插入的新节点是红色的,因为红色的不会影响路径上黑色节点的数量。爸爸是黑色的,皆大欢喜。爸爸和叔叔是红色的,只用改成黑色。爸爸是红色的,叔叔是黑色的,需要进行旋转。以上,就是把树标成红色和黑色的意义,只用简单的判断颜色,就能确定应该怎么调整。
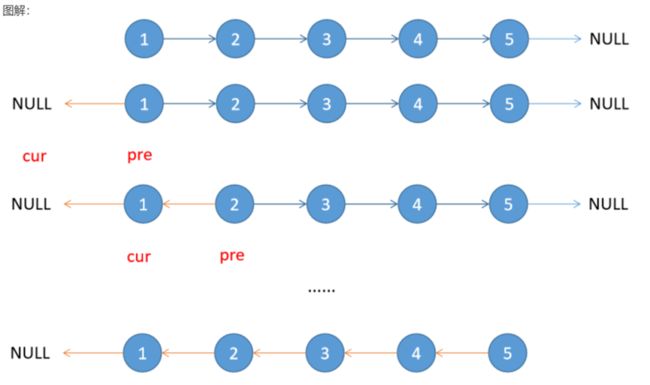
6、反转链表
for pre.Next!=nil{
nxt:=pre.Next
pre.Next=cur
cur=pre
pre=nxt
}
pre.Next=cur
7、回溯
三部曲:
1、回溯函数模板返回值以及参数
2、回溯函数终止条件
3、回溯搜索的遍历过程
for横向遍历,递归纵向遍历
子集问题:解集不能包含重复的子集。for就要从startIndex开始,而不是从0开始!
排列问题:排列问题需要一个used数组。[1,2] 和 [2,1] 是两个集合
去重:
1、
s := []byte(str)
sort.Slice(s,func(i,j int)bool{
return s[i]
2、
if used[i] || (i>0 && s[i]==s[i-1]&& !used[i-1]){
continue
}
8、动态规划
修改字符串/编辑距离
step 1:初始条件: 假设第二个字符串为空,那很明显第一个字符串子串每增加一个字符,编辑距离就加1,这步操作是删除;同理,假设第一个字符串为空,那第二个字符串每增加一个字符,编剧距离就加1,这步操作是添加。
step 2:状态转移: 状态转移肯定是将dp矩阵填满,那就遍历第一个字符串的每个长度,对应第二个字符串的每个长度。如果遍历到str1[i]和 str2[j]的位置,这两个字符相同,这多出来的字符就不用操作,操作次数与两个子串的前一个相同,因此有dp[i][j]=dp[i−1][j−1]dp[i][j] = dp[i - 1][j - 1]dp[i][j]=dp[i−1][j−1];如果这两个字符不相同,那么这两个字符需要编辑,但是此时的最短的距离不一定是修改这最后一位,也有可能是删除某个字符或者增加某个字符,因此我们选取这三种情况的最小值增加一个编辑距离,即
dp[i][j]=min(dp[i−1][j−1],
min(dp[i−1][j],dp[i][j−1]))+1dp[i][j] = min(dp[i - 1][j - 1],
min(dp[i - 1][j],
dp[i][j - 1])) + 1dp[i][j]=min(dp[i−1][j−1],min(dp[i−1][j],dp[i][j−1]))+1
正则表达式匹配
定义状态,并初始化
遍历每个str和pattern中的字符
1、当比较的位pattern[j-1]==‘.’, 或者字符相等匹配,则状态取决于上一次状态
2、对于包含 * 的匹配
当之前位为 ‘.’, 或者字符相等,则匹配
否则只能不匹配
返回状态转移最后的结果
最长的括号子串
9、缓存算法
LRU
Least Recently Used的缩写,即最近最少使用

LFU
Least Frequently Used,最不经常使用策略
结构
两个hashmap
DataMap 用来key来做元素的查找
AtLastMap 用来做哨兵节点的保存
双向链表用来做数据的移动删除和更新
哨兵节点的定义:该访问次数的最后一个节点。k:存储的值, v:访问次数。
双向链表越靠后表示使用频度越高,头节点是访问次数最少的。
GET():
- 先找到key的节点,获取节点值value,取出当前的访问次数access_count
- 查找access_count,判断当前节点是否为哨兵节点。如果是,则删除哨兵节点,令当前节点的前一个节点为哨兵节点,如果没有前一个节点,则删除该键值对。
3、查找access_count+1的哨兵节点,如果找不到,则找access_count的哨兵节点。在双向链表里将本节点插入该节点后
4、设置access_count+1的哨兵节点为自己
PUT(): - 先验证数据是否存在,存在即更新,不存在则插入。更新参考get()方法。
- 判断容量cap,如果容量为0,需要先删除双链表头结点,然后cap++
- 插入节点放在链表头,并设置key=1的哨兵节点
10、回文字符串(KMP)
前缀表: 记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
func getNext(nums []int, s string) {
j:=0
for i := 1; i < len(s); i++ {
for j > 0 && s[i] != s[j] {
j=nums[j-1]
}
if s[i]==s[j]{
j++
}
nums[i]=j
}
}
raft算法:保证集群的数据一致性–https://blog.csdn.net/xxb249/article/details/80787501
回溯:
排列问题,讲究顺序(即 [2, 2, 3] 与 [2, 3, 2] 视为不同列表时),需要记录哪些数字已经使用过,此时用 used 数组;
组合问题,不讲究顺序(即 [2, 2, 3] 与 [2, 3, 2] 视为相同列表时),需要按照某种顺序搜索,此时使用 begin 变量。