代码随想录算法训练营 | day39 动态规划 62.不同路径,63.不同路径Ⅱ
刷题
62.不同路径
题目链接 | 文章讲解 | 视频讲解
题目:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
-
输入:m = 3, n = 7
-
输出:28
示例 2:
-
输入:m = 2, n = 3
-
输出:3
解释: 从左上角开始,总共有 3 条路径可以到达右下角。
-
向右 -> 向右 -> 向下
-
向右 -> 向下 -> 向右
-
向下 -> 向右 -> 向右
示例 3:
-
输入:m = 7, n = 3
-
输出:28
示例 4:
-
输入:m = 3, n = 3
-
输出:6
提示:
-
1 <= m, n <= 100
-
题目数据保证答案小于等于 2 * 10^9
思路及实现
深搜
这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。
注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
如图举例:
此时问题就可以转化为求二叉树叶子节点的个数
大家如果提交了代码就会发现超时了!
来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。
这棵树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
动态规划
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
1.确定dp数组(dp table)以及下标的含义
dpi :表示从(0 ,0)出发,到(i, j) 有dpi条不同的路径。
2.确定递推公式
想要求dpi,只能有两个方向来推导出来,即dpi - 1 和 dpi。
此时在回顾一下 dpi - 1 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dpi同理。
那么很自然,dpi = dpi - 1 + dpi,因为dpi只有这两个方向过来。
3.dp数组的初始化
如何初始化呢,首先dpi一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp0也同理。
4.确定遍历顺序
这里要看一下递推公式dpi = dpi - 1 + dpi,dpi都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dpi的时候,dpi - 1 和 dpi一定是有数值的。
5.举例推导dp数组
如图所示:
以上动规五部曲分析完毕,代码如下:
public static int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
//初始化
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
63.不同路径Ⅱ
题目链接 | 文章讲解 | 视频讲解
题目:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
-
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
-
输出:2 解释:
-
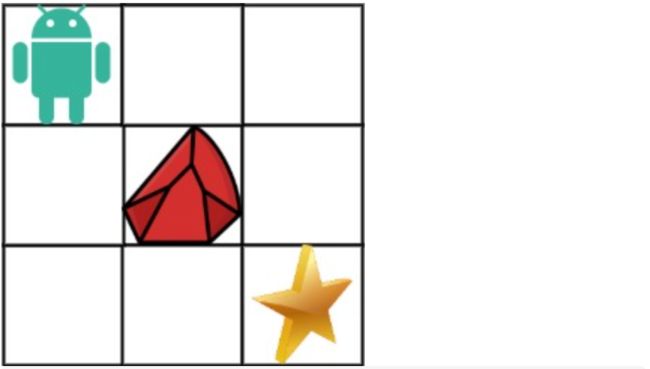
3x3 网格的正中间有一个障碍物。
-
从左上角到右下角一共有 2 条不同的路径:
-
向右 -> 向右 -> 向下 -> 向下
-
向下 -> 向下 -> 向右 -> 向右
-
示例 2:
-
输入:obstacleGrid = [[0,1],[0,0]]
-
输出:1
提示:
-
m == obstacleGrid.length
-
n == obstacleGrid[i].length
-
1 <= m, n <= 100
-
obstacleGridi 为 0 或 1
思路及实现
这道题相对于62.不同路径 就是有了障碍。
第一次接触这种题目的同学可能会有点懵,这有障碍了,应该怎么算呢?
62.不同路径中我们已经详细分析了没有障碍的情况,有障碍的话,其实就是标记对应的dp table(dp数组)保持初始值(0)就可以了。
动规五部曲:
1.确定dp数组(dp table)以及下标的含义
dpi :表示从(0 ,0)出发,到(i, j) 有dpi条不同的路径。
2.确定递推公式
递推公式和62.不同路径一样,dpi = dpi - 1 + dpi。
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
3.dp数组如何初始化
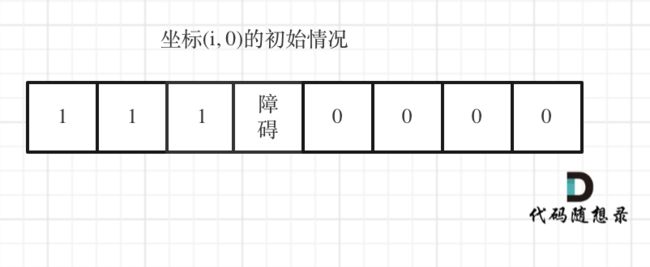
从(0, 0)的位置到(i, 0)的路径只有一条,所以dpi一定为1,dp0也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dpi应该还是初始值0。
如图:
下标(0, j)的初始化情况同理。
注意代码里for循环的终止条件,一旦遇到obstacleGridi == 1的情况就停止dpi的赋值1的操作,dp0同理
4.确定遍历顺序
从递归公式dpi = dpi - 1 + dpi 中可以看出,一定是从左到右一层一层遍历,这样保证推导dpi的时候,dpi - 1 和 dpi一定是有数值。
-
举例推导dp数组
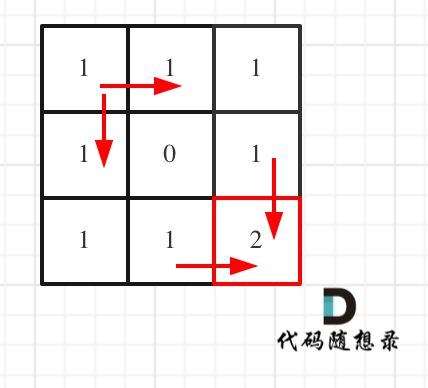
拿示例1来举例如题:
对应的dp table 如图:
如果这个图看不懂,建议再理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
动规五部分分析完毕,对应代码如下:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
//如果在起点或终点出现了障碍,直接返回0
if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
return 0;
}
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
}
}
return dp[m - 1][n - 1];
}
}// 空间优化版本
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[] dp = new int[n];
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 0; j < n; j++) {
if (obstacleGrid[i][j] == 1) {
dp[j] = 0;
} else if (j != 0) {
dp[j] += dp[j - 1];
}
}
}
return dp[n - 1];
}
}