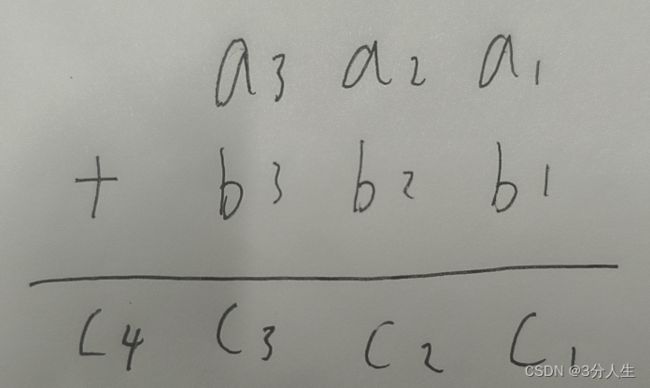高精度运算(加,乘,阶乘)
概念
高精度所谓数据比较大,在计算中我们会遇到10的几十次方甚至几百次方,一般的数据类型是储存不下,所以需要特殊处理。
1.当输入的数据比较大时,可以采用字符串方式输入,然后再把每一位数字存在数组里面,如下
#include
#include
int main()
{
char a[100];
int b[100], k, i;
scanf("%s", a);
k = strlen(a);
for (i = 0; i < k; i++)
{
b[i] = a[i] - '0';
}
return 0;
} 2.对高精度进型加法时就是模仿进位过程,乘法也是如此。
而高精度的计算就是模拟这个计算过程。废话不多说下面看例题:
例题1:洛谷P1601 A+B Problem(高精)
题目描述
高精度加法,相当于 a+b problem,不用考虑负数。
输入格式
分两行输入。a,b≤10^500。
输出格式
输出只有一行,代表 a+b 的值。
输入 #1
1 1
输出 #1
2
输入 #2
1001 9099
输出 #2
10100
说明/提示
20%20% 的测试数据,0≤a,b≤10^9;
40%40% 的测试数据,0 ≤a,b≤10^18。
解题思路
输入用字符串,然后把每一位数存放的一个数组进行操作,模仿加法过程,考虑进位的情况,下面上代码
//P1601 A+B Problem(高精)
#include
#include
char a[3000], b[3000];//定义两个字符串数组表示a,b
int x[3000] = { 0 }, y[3000] = { 0 }, z[3000] = { 0 };//x,y数组用来储存a,b的每一位数,z用来储存a,b和的每一位数
int main()
{
int k, i, j, h;
scanf("%s %s", a, b);//输入a,b的值
k = strlen(a);//求出a的位数
h = strlen(b);//求出b的位数
for (i = 0; i < k; i++)//a的每一位数放入x数组中
x[i] = a[k - i - 1] - '0';
for (i = 0; i < h; i++)//b的每一位数放入x数组中
y[i] = b[h - i - 1] - '0';
int s = k > h ? k : h;//求出a,b中哪个数位数更多
s += 1;//加一考虑两数之和进位的情况
for (i = 0; i < s; i++)
{
z[i] += x[i] + y[i];//每一位数两两对应相加
if (z[i] > 9)//大于9考虑进位
{
z[i + 1]++;
z[i] -= 10;
}
}
if (z[s - 1] == 0)//考虑两数相加是否进位
s--;
for (i = s - 1; i >= 0; i--)//输出答案
printf("%d", z[i]);
return 0;//圆满结束
}
例题2:洛谷P1303 A*B Problem
题目描述
给出两个非负整数,求它们的乘积。
输入格式
输入共两行,每行一个非负整数。
输出格式
输出一个非负整数表示乘积。
输入输出样例
输入 #1
1 2
输出 #1
2
说明/提示
每个非负整数不超过 10^2000。
解题思路
思路还是和加法类似,输入用字符串,然后把每一位数存放的一个数组进行操作,模仿乘法过程,考虑进位的情况,下面上代码
//P1303 A* B Problem
#include
#include
char a[3000], b[3000];//定义两个字符串数组表示a,b
long long x[3000] = { 0 }, y[3000] = { 0 }, z[5000000] = { 0 };//x,y数组用来储存a,b的每一位数,z用来储存a,b积的每一位数
int main()
{
int k, i, j, h;
scanf("%s %s", a, b);//输入a,b的值
k = strlen(a);//求出a的位数
h = strlen(b);//求出b的位数
for (i = 0; i < k; i++)//a的每一位数放入x数组中
x[i] = a[k - i - 1] - 48;
for (i = 0; i < h; i++)//b的每一位数放入y数组中
y[i] = b[h - i - 1] - 48;
int q, s = 0;//q,s用来控制两个数相乘其中一个数的各位乘完后下一个数乘时往前移动一位
for (i = 0; i < k; i++)
{
q = s;
for (j = 0; j < h; j++)
{
z[q] += x[i] * y[j];//之所以要加等于考虑后面可能有进位的情况
if (z[q] > 9)//进位
{
z[q+1] += z[q] / 10;
z[q] = z[q] % 10;
}
q++;
}
s++;
}
long long f = k + h + 1;//两个数相乘,乘积的位数一定小于等于两个数的位数的和加1
while (z[f] == 0 && f > 0)//判断是否有前导0
f--;
for (i = f; i >= 0; i--)//输出答案
printf("%lld", z[i]);
return 0;
}
例题3:洛谷P1009[NOIP1998 普及组] 阶乘之和
题目描述
用高精度计算出 S=1!+2!+3!+⋯+n!(n≤50)。
其中 ! 表示阶乘,定义为 n!=n×(n−1)×(n−2)×⋯×1。例如,5!=5×4×3×2×1=120。
输入格式
一个正整数 n。
输出格式
一个正整数 S,表示计算结果。
输入 #1
3
输出 #1
9
说明/提示
对于 100% 的数据,1≤n≤50。
解题思路
本题既有乘法又有加法,显然就是高精乘+高精加,就是把高精乘的模板套上去接着套高精加的模板,这题1~n每个数的阶乘可以用一个二维数组来储存
废话不多说,上代码
//P1009[NOIP1998 普及组] 阶乘之和
#include
unsigned long long a[106][250] = { 0 };//定义二维数组储存1-n的每一个数的阶乘
unsigned long long n, i, j, k, b[250] = { 0 }, c[250] = { 0 };//b数组用来过度每一个数的阶乘运算,c数组用来求出加法运算
int main()
{
a[1][1] = 1; k = 1;//初始化
scanf("%llu", &n);
//阶乘计算过程+-------------------------------------------------------+
for (i = 2; i <= n; i++)
{
for (j = 1; j <= k; j++)
{
b[j] = a[i-1][j];
}
for (j = 1; j <= k; j++)//注意a[i]=a[i-1]*i,a[i-1]此时就是b数组
{
a[i][j+1] += (b[j] * i) / 10;
a[i][j] += (b[j] * i) % 10;
}
if (a[i][k+1] != 0)//考虑结果是否进位
{
k++;
}
}
//阶乘之和计算过程+----------------------------------------------------------+
for (i = 1; i <= k; i++)
{
for (j = 1; j <= n; j++)
{
c[i] += a[j][i];//统计每一竖排的和
}
c[i + 1] += c[i] / 10;//考虑进位
c[i] = c[i] % 10;
}
if (c[k + 1] != 0)//考虑结果是否进位
k++;
for (i = k; i >= 1; i--)//输出答案
printf("%llu", c[i]);
return 0;
}