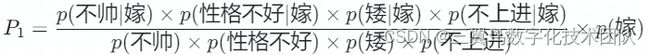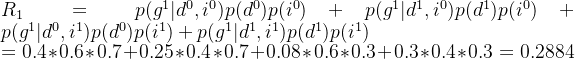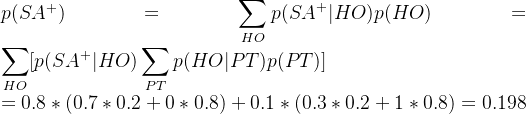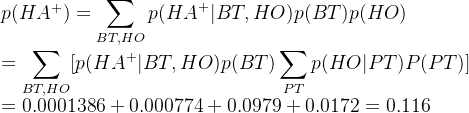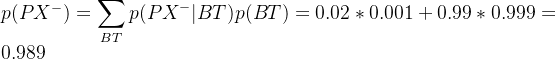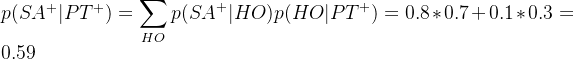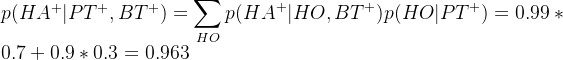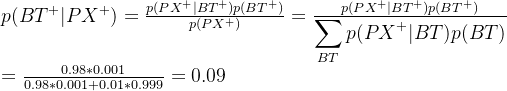机器学习算法基础——分类模型(一)
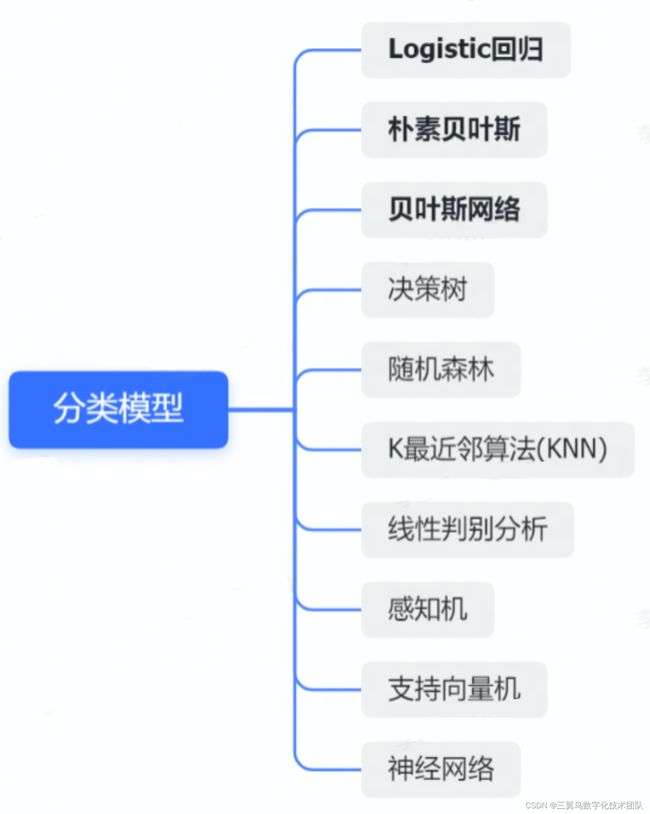
什么是分类?
举一个简单的例子,一个小朋友面前有两个果篮,一个是放橘子,一个是放苹果,你给他一个水果(橘子或苹果的一种),然后希望他根据以往的经验和学习信息(外形、颜色、纹路、触感等可观测特征)来判断这个水果该放进哪个果篮?
分类就是机器通过比较事物之间的相似性,把具有某些共同点或相似特征的事物归属于一个集合的逻辑方法。
1 Logistic回归模型
Logistic回归又称对数几率回归,是机器学习中的一种常用的线性分类模型,虽然名字中带有回归,但是它是一种实打实的分类器。Logistic回归基本思想是在线性回归的基础上,使用Sigmoid函数,将线性模型的结果压缩到[0,1]之间,使其拥有概率意义,实现值到概率的转换。
1.1 算法原理
1.1.1 Sigmoid函数(S函数)
在使用线性模型实现二分类任务时,通常需要找到一个连续可微的映射函数将线性结果转化为0/1值,而Sigmoid函数满足以上条件,其函数表达式如下
![]()
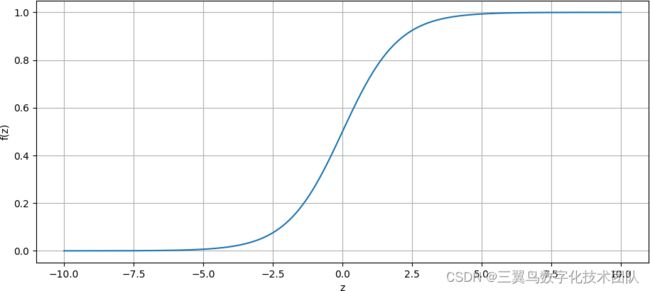
Sigmoid函数图像如下
由上图可知,sigmoid函数会把线性回归的结果映射到区间 [0,1],假设以0.5为阈值,默认会把概率小于0.5的记为0,大于等于0.5的记为1。
1.1.2 原理简介
给定一组由输入 x 和输出 y 构成的训练集 ![]() ,其中
,其中![]() ,类别标签
,类别标签 ![]() ,线性回归方程矩阵形式可定义为
,线性回归方程矩阵形式可定义为
结合sigmoid函数,上式估计向量可映射为
![]()
与线性回归以残差平方和作为损失函数不同,Logistic回归使用极大似然方法对参数进行估计求解。极大似然估计的核心思想可以理解为,如果一个事件发生了,那么该事件理论上就是发生概率最大的那个事件,为了使似然函数值最大,也就是使该事件成为发生概率最大的那个事件。那么,对于抽样数据集D就是一个发生概率最大的事件,我们将概率值 ![]() 其对应正例
其对应正例 ![]() ,
,![]() 对应反例
对应反例 ![]() ,可构造似然函数
,可构造似然函数
对等式两侧求对数并取负
此时极大似然函数最大值就转化为求其最小值,梯度向量代数式为
矩阵形式为
![]()
最后利用批量梯度下降法或牛顿迭代法即可求得最优解。
1.2 企业财务风险诊断案例
本案例通过分析企业各项财务指标,使用Logistic回归预测企业是否存在财务风险问题。本文献摘自《系统科学学报》“基于Logistic回归模型的企业财务风险诊断研究”。
https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C44YLTlOAiTRKibYlV5Vjs7iy_Rpms2pqwbFRRUtoUImHdczUT4ihhHbWLY_AyVopRYQHaEQ-iwaw0oQMqPvLVR_&uniplatform=NZKPT
文中使用 2018 年和 2019年由于连续两年亏损导致财务状况异常的共 74 家上市公司财务数据作为存在财务风险的样本数据。将企业存在财务风险记为1,不存在财务风险记为0。具体分析流程如下:
(1)财务指标的获取
由于问题企业通常存在偿债压力较大、业务增长放缓甚至衰退、周转能力下降等特点,所以从企业偿债、增长、经营三个方面出发初步选取了相应的 17 个财务指标进行分析。选取指标如下表所示。
(2) 财务指标筛选
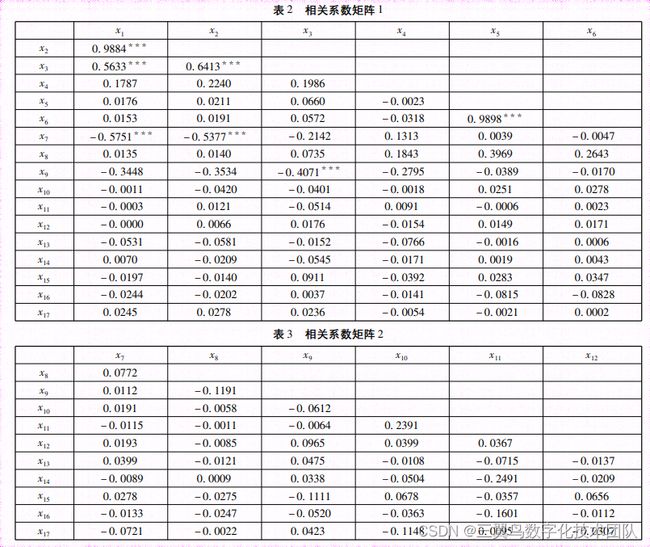
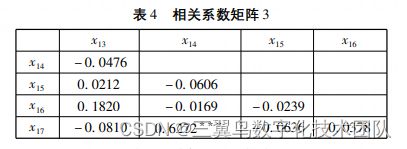
在对企业财务风险指标进行回归分析之前,考虑到不同财务指标可能存在多重共线性,因此需要使用相关系数判定这 17 个变量的相关性。
由相关系数矩阵可知,变量(x1,x2)、(x5 ,x6)呈现出高度的相关性,且( x1,x3)、(x1,x7)、(x2,x3)、(x2,x7)、(x14,x17)亦呈现相关性。当两个或两个以上变量之间的相关性较强的时候,不可将他们同时作为解释变量放入模型,这里只需要选择其中一个变量作为解释变量。
此外,通过对正常公司和财务风险公司财务数据的对比,识别出企业出现财务风险影响最明显的几个指标,即两者财务指标具有显著性差异项。对样本数据实施逐步选择法进行回归,进一步得出在识别企业财务风险过程中具有显著性的变量,显著性水平以0.05为界,其结果如表 5 所示。
得到财务风险公司与正常公司在营运资金与借款比(x4) 、利息保障倍数(x5) 、资产负债率(x9) 、可持续增长率(x12) 、应收账款周转率 (x13)五项指标具有显著性差异,大大简化了问题的规模。
(3)模型构建
通过数据学习这几个显著相关变量,可构建出企业财务风险识别模型如下
![]()
当prob>=0.5,则认定企业存在财务风险(1),若 prob<0.5 认定企业不存在财务风险(0)。
1.3 考试合格率案例
对班上学生进行两门课程的考试,未清洗前各科成绩统计如下表。前两列分别代表学生科目1和科目2的成绩,第三列数字中0代表总成绩考核不合格,1代表总成绩考核合格。我们的任务是根据这些数据建立一个Logistic回归模型对学生总成绩进行分类预测。
(1)数据线性归一化处理
![]()
(2)建立Logistic回归模型
![]()
(3)初始化参数 ![]() ,设置学习率
,设置学习率 ![]() ,最大迭代步数
,最大迭代步数 ![]() ,使用批量梯度下降算法求得参数。
,使用批量梯度下降算法求得参数。
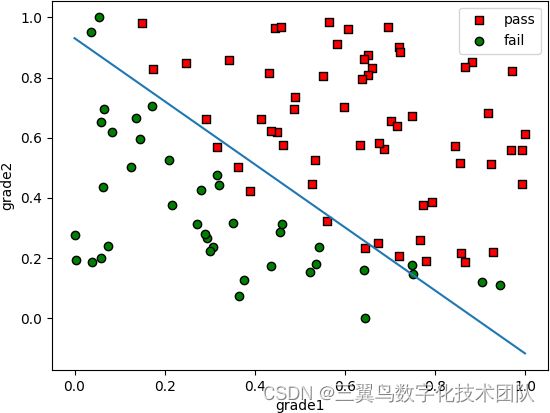
回归模型计算结果如下:
![]()
本模型的准确率为90%
2 朴素贝叶斯模型
朴素贝叶斯模型是基于贝叶斯定理和类特征条件独立性假设的分类算法,是一种典型的基于概率理论的分类器。基本思想如下:对于给定的训练数据集,朴素贝叶斯首先基于特征条件独立假设学习输入和输出的联合概率分布;然后基于此模型,对给定的输入实例,利用贝叶斯公式求出最大的后验概率。朴素贝叶斯法实现简单,学习与预测的效率都很高。
2.1 原理简介
贝叶斯定理计算公式如下
![]()
-
p(A)、p(B) 先验概率:一个事件单独发生的可能性,通过样本数据或以往经验中总结得到的概率
-
p(A|B) 后验概率:通过贝叶斯公式,结合样本数据对先验概率修正后的概率值,修正后的概率更加接近于真实概率。
-
p(B|A) 条件概率:又叫做似然概率,一般是通过历史数据统计获得
朴素贝叶斯原理:
待分类对象target具有特征属性 ![]() ,类别标签集合为
,类别标签集合为 ![]() ,根据(8)式贝叶斯公式可知target属于类别
,根据(8)式贝叶斯公式可知target属于类别 ![]() 的概率为
的概率为
![]()
在朴素贝叶斯算法中,待分类对象的每个特征属性都是条件独立的,由贝叶斯公式
在 ![]() 个结果中取最大值即为target所属类别
个结果中取最大值即为target所属类别
![]()
为方便理解,式(10)可理解为
高斯朴素贝叶斯:
在计算条件概率时,对于离散的数据特征可以使用大数定理(频率代替概率的思想)。但是,怎么处理连续的特征呢?这里我们一般使用高斯朴素贝叶斯。
所谓高斯朴素贝叶斯,就是假设每个连续特征属性都服从高斯分布,可以使用高斯概率密度函数直接计算条件概率值
![]() 为在类别
为在类别 ![]() 的条件下,特征
的条件下,特征 ![]() 的方差;
的方差;
![]() 为在类别
为在类别 ![]() 的条件下,特征
的条件下,特征 ![]() 的均值;
的均值;
此时,我们只需要计算连续特征的均值和方差即可。
2.2 婚嫁案例
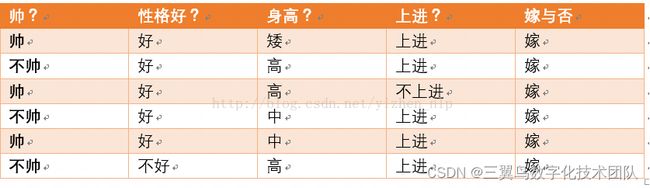
测试数据:
| 不帅 |
性格不好 |
矮 |
不上进 |
? |
结合贝叶斯公式,我们可以得到如下概率公式:
(1)计算 ![]() 值
值
根据朴素贝叶斯特征独立分布特点,可知
先验概率:
嫁的样本数据如下:
条件概率:
可得
(2)计算 ![]() 值
值
同理我们可以得到 ![]() 计算结果:
计算结果:
显然,![]() ,所以当一个男生(不帅,性格不好,矮,不上进),多数女生心中已经有了一个答案——不嫁!
,所以当一个男生(不帅,性格不好,矮,不上进),多数女生心中已经有了一个答案——不嫁!
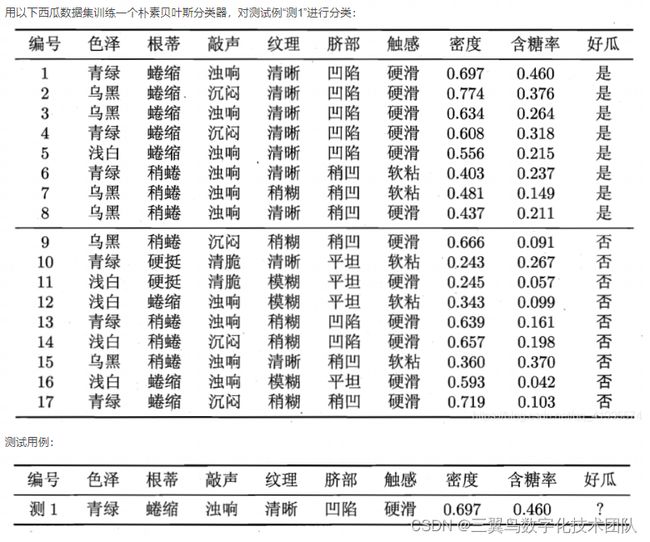
2.3 西瓜分类案例
3 贝叶斯网络
3.1 原理简介
朴素贝叶斯最大的特点是满足特征条件独立性假设,但在现实情况中,特征之间通常会具有一定的相关性,使得朴素贝叶斯性能受到一定的限制。下面介绍一另种贝叶斯算法——贝叶斯网络。
贝叶斯网的网络结构是一个有向无环图,其中每个结点代表一个属性,结点间的连线代表属性间的条件概率依赖关系。根据网络图可以得到联合概率
![]()
不失一般性,令图 G 为定义在 ![]() 上的一个贝叶斯网络,其联合概率分布可以表示为各个节点的条件概率分布的乘积
上的一个贝叶斯网络,其联合概率分布可以表示为各个节点的条件概率分布的乘积
![]()
![]() 代表属性
代表属性 ![]() 的父节点,
的父节点,![]() 代表节点条件概率。
代表节点条件概率。
贝叶斯网络相比朴素贝叶斯算法更为复杂,但贝叶斯网络是一种模拟人的认知思维的推理模式,用一组条件概率函数以及有向无环图对不确定性因果推理关系建模,因此其具有更高的实用价值。
3.2 学生推荐信案例
根据上图可知贝叶斯网络的两个组成要素:(1) 贝叶斯网络图的结构:显示了各随机变量之间的关系;(2) 条件概率表:每个变量对其父节点的条件概率,这些知识可以通过专家经验填入,也可以通过历史数据训练得到。有了这些数据,贝叶斯网络可以实现:
- 全概率公式进行因果预测:(1)没有任何证据的条件下,推理结果的发生概率;(2)已知一定原因的条件下,推理结果的发生概率
- 贝叶斯公式进行逆向诊断:已知发生了某些结果,由结果反推造成该结果的原因以及发生的概率
3.2.1 因果预测
1. 任何信息都不知道的条件下,推断结果发生的概率
问题一:某生获得推荐信的概率为多少?
根据贝叶斯网络结构图,由全概率公式可得知获得推荐信的概率为
展开为
![]()
其中
![]()
将概率表对应数值带入得
![]()
在任何信息都不知道的情况下,该同学获得推荐信的概率为0.502。
问题二:某生考试获得良好的概率 ![]()
由全概率公式得
所以该生获得良好的概率为0.288
2.已知一定原因,推理结果发生的概率
问题一:现已知该生智商不高 ![]() ,推断其获得推荐信的概率
,推断其获得推荐信的概率 ![]()
问题二:在问题三的基础上,进一步得知考试比较简单 $$$$,推断其获得推荐信的概率![]()
3.2.2 逆向诊断
问题一:该生具有高智商的先验概率(边缘概率)$$p(i^1)=0.3$$,假设该生成绩为$$g^2$$,求该生具有高智商的概率?
由贝叶斯公式可知
通过数据计算先验概率由0.3修正为0.079,因此,该生大概率不具有高智商。
问题二:在收到推荐信的前提下,考试难度大的概率?
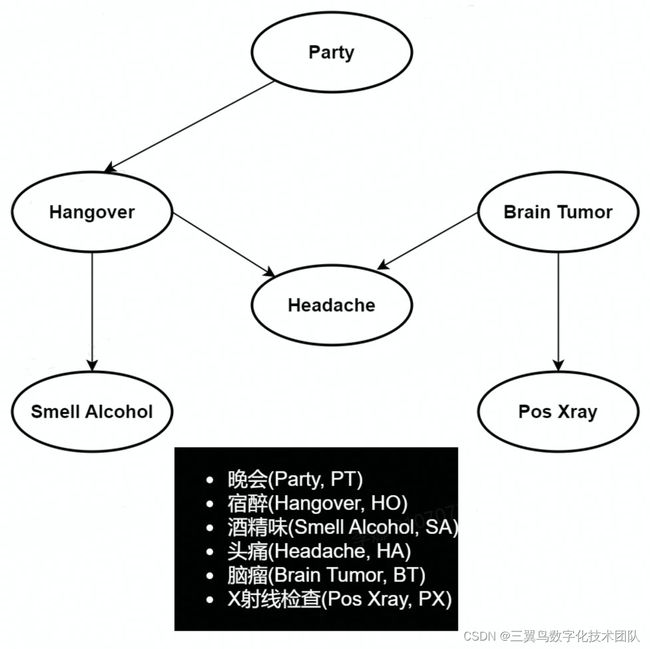
3.3 疾病诊断
3.3.1 因果预测
1. 任何信息都不知道的条件下,推断结果发生的概率
问题一:计算某人身上有酒精味的概率为多少?
问题二:计算某人头痛的概率为多少?
问题三:计算某人X射线呈阴性的概率为多少?
那么,阳性的概率就是 ![]()
2. 已知一定原因,推理结果发生的概率
问题一:参加晚会的前提下,计算某人身上有酒精味的概率为多少?
可见参加晚会比起参加晚会信息未知,身上有酒精味的几率会由0.198提升至0.59。
问题二:参加晚会和患脑瘤的前提下,计算某人头痛的概率为多少?
相比任何证据都没有前提下头痛概率0.116,参加晚会和患脑瘤的都发生,某人头痛的概率增加到0.963
3.3.2 逆向诊断
问题一:X射线呈阳性,计算患脑瘤的概率为多少?
问题二:头痛的前提下,计算患脑瘤的概率为多少?
可见X射线呈阳性相比头痛更容易患脑瘤。
4. 团队介绍
「三翼鸟数字化技术平台-前端开发能力平台」通过持续搭建和完善前端研发流程、跨端复用能力、通用能力、规范和机制,建立标准化、平台化的前端研发体系,致力于提升团队前端开发能力、研发效率和用户体验,同时负责内容交互、场景交互、小程序、海外app等前端业务开发。
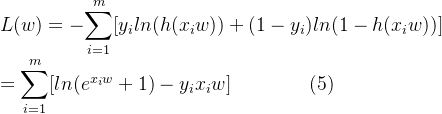
![\frac{\partial}{\partial{w}}L(w)= {\displaystyle \sum_{i=1}^m}[x_i(h(x_iw)-y_i)] \qquad\qquad (6)](http://img.e-com-net.com/image/info8/50773507e5474198bc8adce9a8d3ccce.png)



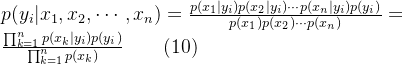
![p(x_k|y_i)=\frac{1}{\sqrt{2\pi\sigma^2_{x_k|y_i}}}exp \bigg[-\frac{\big(x_i-\mu_{x_k|y_i}\big)^2}{2\sigma^2_{x_k|y_i}}\bigg] \qquad (13)](http://img.e-com-net.com/image/info8/e11e171790614056b8ae08b6b645e451.png)